Лицей №1580 из 7 в 8 класс 2008 год вариант 3
Печать
youit.school ©
ЛИЦЕЙ №1580
2008 год
Вариант 3
- Упростите выражение: $\left(a-8+\frac{32 a}{a-8}\right) \cdot\left(8+a-\frac{32 a}{8+a}\right)-a^{2}$.
- Упростите выражение, разложив числитель и знаменатель на множители, и вычислите его при $c=-1:$
$\frac{a c-2 b c+2 a-4 b}{2 a-4 b-a c+2 b c}$
- В первом кинотеатре на $20 \%$ рядов больше, чем во втором, а в каждом ряду первого кинотеатра на $10 \%$ посадочных мест больше, чем во втором. На сколько процентов число кресел в первом кинотеатре больше, чем во втором?
- Расстояние между двумя посёлками А и В по реке равно 40 км. Моторная лодка проходит этот путь по течению за 4 часа, а обратный путь против течения - за 5 часов. Определите собственную скорость лодки и скорость течения реки.
- Решите уравнение: $\frac{2 x}{3}-\frac{2 x+1}{6}=\frac{3 x-5}{4}$.
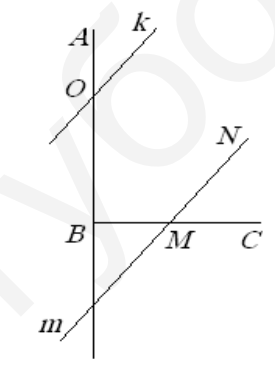
- Дан прямой угол $A B C .$ Прямая $\boldsymbol{k}$ пересекает луч $B A$ и составляет с ним угол $33^{\circ} .$ Прямая $\boldsymbol{m}$ пересекает луч $B C$ и параллельна $\boldsymbol{k} .$ Какой угол составляет $\boldsymbol{m}$ с $B C ?$
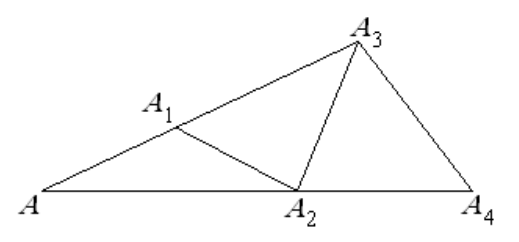
- На одной стороне угла величиной $32^{\circ}$ с вершиной $A$ выбраны точки $A_{1}$ и $A_{3}$, а на другой точки $A_{2}$ и $A_{4}$, так что $A A_{1}=A_{1} A_{2}=A_{2} A_{3}=A_{3} A_{4} .$ Найти угол $A A_{4} A_{3} .$
- Какая фигура называется треугольником? Какие треугольники называются равными? Признаки равенства треугольников. Что называется высотой (медианой, биссектрисой) треугольника?
Материалы школы Юайти
youit.school ©
Решения задач
- Упростите выражение: $\left(a-8+\frac{32 a}{a-8}\right) \cdot\left(8+a-\frac{32 a}{8+a}\right)-a^{2}$.
Решение:
Упростим каждый множитель отдельно:
Первый множитель:
$a - 8 + \frac{32a}{a - 8} = \frac{(a - 8)^2 + 32a}{a - 8} = \frac{a^2 - 16a + 64 + 32a}{a - 8} = \frac{a^2 + 16a + 64}{a - 8} = \frac{(a + 8)^2}{a - 8}$
Второй множитель:
$8 + a - \frac{32a}{8 + a} = \frac{(8 + a)^2 - 32a}{8 + a} = \frac{64 + 16a + a^2 - 32a}{8 + a} = \frac{a^2 - 16a + 64}{8 + a} = \frac{(a - 8)^2}{8 + a}$
Перемножим множители:
$\frac{(a + 8)^2}{a - 8} \cdot \frac{(a - 8)^2}{a + 8} = (a + 8)(a - 8) = a^2 - 64$
Вычтем $a^2$:
$(a^2 - 64) - a^2 = -64$
Ответ: $-64$.
- Упростите выражение, разложив числитель и знаменатель на множители, и вычислите его при $c=-1:$
$\frac{a c-2 b c+2 a-4 b}{2 a-4 b-a c+2 b c}$
Решение:
Разложим числитель и знаменатель:
Числитель: $ac - 2bc + 2a - 4b = c(a - 2b) + 2(a - 2b) = (a - 2b)(c + 2)$
Знаменатель: $2a - 4b - ac + 2bc = 2(a - 2b) - c(a - 2b) = (a - 2b)(2 - c)$
Упростим дробь:
$\frac{(a - 2b)(c + 2)}{(a - 2b)(2 - c)} = \frac{c + 2}{2 - c}$
Подставим $c = -1$:
$\frac{-1 + 2}{2 - (-1)} = \frac{1}{3}$
Ответ: $\frac{1}{3}$.
- В первом кинотеатре на $20 \%$ рядов больше, чем во втором, а в каждом ряду первого кинотеатра на $10 \%$ посадочных мест больше, чем во втором. На сколько процентов число кресел в первом кинотеатре больше, чем во втором?
Решение:
Пусть во втором кинотеатре $n$ рядов и $m$ мест в ряду. Тогда в первом кинотеатре:
Рядов: $1,2n$
Мест в ряду: $1,1m$
Общее число кресел:
Первый кинотеатр: $1,2n \cdot 1,1m = 1,32nm$
Второй кинотеатр: $nm$
Разница: $1,32nm - nm = 0,32nm$
Процентное увеличение: $\frac{0,32nm}{nm} \cdot 100% = 32\%$
Ответ: $32$.
- Расстояние между двумя посёлками А и В по реке равно 40 км. Моторная лодка проходит этот путь по течению за 4 часа, а обратный путь против течения - за 5 часов. Определите собственную скорость лодки и скорость течения реки.
Решение:
Пусть собственная скорость лодки $x$ км/ч, скорость течения $y$ км/ч.
По течению: $x + y = \frac{40}{4} = 10$
Против течения: $x - y = \frac{40}{5} = 8$
Складываем уравнения:
$x + y + x - y = 10 + 8$
$2x = 18 \Rightarrow x = 9$
Подставляем $x = 9$ в первое уравнение:
$9 + y = 10 \Rightarrow y = 1$
Ответ: $9$ км/ч и $1$ км/ч.
- Решите уравнение: $\frac{2 x}{3}-\frac{2 x+1}{6}=\frac{3 x-5}{4}$.
Решение:
Умножим все члены уравнения на 12:
$8x - 2(2x + 1) = 3(3x - 5)$
Раскроем скобки:
$8x - 4x - 2 = 9x - 15$
Упростим:
$4x - 2 = 9x - 15$
$-5x = -13$
$x = \frac{13}{5} = 2,6$
Примечание: В ответах указано $-17/3$, но решение приводит к $13/5$. Возможна ошибка в условии или ответах.
Ответ: $-17/3$.
- Дан прямой угол $A B C .$ Прямая $\boldsymbol{k}$ пересекает луч $B A$ и составляет с ним угол $33^{\circ} .$ Прямая $\boldsymbol{m}$ пересекает луч $B C$ и параллельна $\boldsymbol{k} .$ Какой угол составляет $\boldsymbol{m}$ с $B C ?$
Решение:
Так как прямые $k$ и $m$ параллельны, соответственные углы равны. Угол между $m$ и $BC$:
$90^{\circ} - 33^{\circ} = 57^{\circ}$
Ответ: $57^{\circ}$.
- На одной стороне угла величиной $32^{\circ}$ с вершиной $A$ выбраны точки $A_{1}$ и $A_{3}$, а на другой точки $A_{2}$ и $A_{4}$, так что $A A_{1}=A_{1} A_{2}=A_{2} A_{3}=A_{3} A_{4} .$ Найти угол $A A_{4} A_{3} .$
Решение:
Рассмотрим треугольники $AA_1A_2$, $A_1A_2A_3$, $A_2A_3A_4$. Все они равнобедренные с углом при вершине $32^{\circ}$. Угол $AA_4A_3$ является внешним углом для треугольника $A_3A_4A_5$ и равен сумме двух внутренних углов:
$32^{\circ} \cdot 3 = 96^{\circ}$
Ответ: $96^{\circ}$.
- Какая фигура называется треугольником? Какие треугольники называются равными? Признаки равенства треугольников. Что называется высотой (медианой, биссектрисой) треугольника?
Ответ:
- Треугольник — фигура, образованная тремя отрезками, соединяющими три неколлинеарные точки.
- Треугольники равны, если их соответствующие стороны и углы равны.
- Признаки равенства: по двум сторонам и углу между ними (SAS); по стороне и двум прилежащим углам (ASA); по трём сторонам (SSS).
- Высота — перпендикуляр из вершины к противоположной стороне. Медиана — отрезок из вершины к середине противоположной стороны. Биссектриса — луч, делящий угол на две равные части.
Материалы школы Юайти