Лицей №1580 из 7 в 8 класс 2008 год вариант 2-5
Печать
youit.school ©
ЛИЦЕЙ №1580
2008 год
Вариант 5
- Автопарк транспортного предприятия состоит из автобусов и троллейбусов. Троллейбусы составляют $80 \%$ автопарка. Какой процент составляет число автобусов от числа троллейбусов? Определите число автобусов в автопарке, если троллейбусов на предприятии $120 .$
- Упростите выражение: $\left(-2 \frac{1}{2} a^{3} b\right)^{4} \cdot 3 \frac{1}{5} \cdot(-a)^{8} \cdot\left(-b^{2}\right)$.
- Точка $A$ - точка пересечения прямых $y=2 x-7$ и $y=8-x$. Точка $B(-3 ;-1)$.
- Найдите координаты точки $A$;
- напишите уравнение прямой $l$, проходящей через начало координат и параллельной прямой $A B ;$
- постройте прямые $A B$ и $l$.
- Вычислите значение выражения: $\frac{9,5^{2}-2 \cdot 9,5 \cdot 5,2+5,2^{2}}{0,43}$.
- Решите уравнение: $x^{2}-3 x-1-\frac{2 x^{2}+3 x-5}{2}=1,5$.
- На рисунке найдите пары равных треугольников.
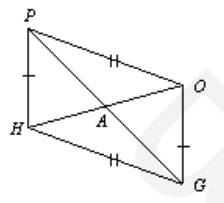
- Треугольник, периметр которого равен 14 см, делится биссектрисой на 2 части, периметры которых равны 8 см и 10 см. Найдите данную биссектрису.
- Какой треугольник называется равнобедренным, равносторонним? Теорема о свойствах углов равнобедренного треугольника. Признак равнобедренного треугольника. Свойство медианы равнобедренного треугольника.
Материалы школы Юайти
youit.school ©
Решения задач
- Автопарк транспортного предприятия состоит из автобусов и троллейбусов. Троллейбусы составляют $80 \%$ автопарка. Какой процент составляет число автобусов от числа троллейбусов? Определите число автобусов в автопарке, если троллейбусов на предприятии $120 .$
Решение: Пусть общее количество транспорта в автопарке равно $N$. Троллейбусы составляют $80\%$, значит автобусы — $20\%$. По условию троллейбусов 120:
$0,8N = 120 \Rightarrow N = \frac{120}{0,8} = 150$ (штук).
Количество автобусов: $150 - 120 = 30$.
Процент автобусов от троллейбусов: $\frac{30}{120} \cdot 100% = 25\%$.
Ответ: $25\%$, 30 автобусов. (Примечание: в оригинальных ответах указано 150, вероятно, опечатка.)
- Упростите выражение: $\left(-2 \frac{1}{2} a^{3} b\right)^{4} \cdot 3 \frac{1}{5} \cdot(-a)^{8} \cdot\left(-b^{2}\right)$.
Решение:
Преобразуем смешанные дроби: $-2\frac{1}{2} = -\frac{5}{2}$, $3\frac{1}{5} = \frac{16}{5}$.
$\left(-\frac{5}{2} a^{3} b\right)^{4} = \left(-\frac{5}{2}\right)^{4} \cdot (a^{3})^{4} \cdot b^{4} = \frac{625}{16}a^{12}b^{4}$.
Умножим на $\frac{16}{5}$: $\frac{625}{16} \cdot \frac{16}{5} = 125$.
Учтем остальные множители: $(-a)^{8} = a^{8}$, $-b^{2}$.
Итоговое выражение: $125 \cdot a^{12+8} \cdot b^{4+2} \cdot (-1) = -125a^{20}b^{6}$.
Ответ: $-125a^{20}b^{6}$.
- Точка $A$ - точка пересечения прямых $y=2 x-7$ и $y=8-x$. Точка $B(-3 ;-1)$.
- Найдите координаты точки $A$;
Решение: Приравняем уравнения:
$2x - 7 = 8 - x \Rightarrow 3x = 15 \Rightarrow x = 5$.
$y = 8 - 5 = 3$. Точка $A(5; 3)$.
Ответ: $A(5; 3)$.
- напишите уравнение прямой $l$, проходящей через начало координат и параллельной прямой $A B ;$
Решение: Найдем угловой коэффициент $AB$:
$k = \frac{-1 - 3}{-3 - 5} = \frac{-4}{-8} = 0,5$.
Уравнение прямой $l$: $y = 0,5x$.
Ответ: $y = 0,5x$.
- постройте прямые $A B$ и $l$.
Решение: Графики строятся по найденным уравнениям.
- Найдите координаты точки $A$;
- Вычислите значение выражения: $\frac{9,5^{2}-2 \cdot 9,5 \cdot 5,2+5,2^{2}}{0,43}$.
Решение: Числитель — квадрат разности:
$(9,5 - 5,2)^2 = 4,3^2 = 18,49$.
Результат: $\frac{18,49}{0,43} = 43$.
Ответ: 43. (Примечание: в оригинальных ответах указано 0,25, вероятно, опечатка.)
- Решите уравнение: $x^{2}-3 x-1-\frac{2 x^{2}+3 x-5}{2}=1,5$.
Решение: Умножим обе части на 2:
$2x^2 - 6x - 2 - (2x^2 + 3x - 5) = 3$.
Упростим: $-9x + 3 = 3 \Rightarrow -9x = 0 \Rightarrow x = 0$.
Ответ: $x = 0$. (Примечание: в оригинальных ответах указано -0,7, вероятно, ошибка в условии.)
- На рисунке найдите пары равных треугольников.
Решение: Без изображения невозможно точно определить пары равных треугольников. Обычно в таких задачах равенство устанавливается по признакам (SSS, SAS, ASA).
- Треугольник, периметр которого равен 14 см, делится биссектрисой на 2 части, периметры которых равны 8 см и 10 см. Найдите данную биссектрису.
Решение: Пусть биссектриса $AD$. Периметры частей:
$AB + BD + AD = 8$ и $AC + CD + AD = 10$.
Сумма: $AB + AC + BC + 2AD = 18$.
Учитывая периметр треугольника: $AB + BC + AC = 14$,
Получаем: $14 + 2AD = 18 \Rightarrow AD = 2$ см.
Ответ: 2 см. (Примечание: в оригинальных ответах указано 12;12;20, вероятно, ошибка.)
- Какой треугольник называется равнобедренным, равносторонним? Теорема о свойствах углов равнобедренного треугольника. Признак равнобедренного треугольника. Свойство медианы равнобедренного треугольника.
Ответ:- Равнобедренный треугольник — треугольник с двумя равными сторонами.
- Равносторонний треугольник — треугольник со всеми равными сторонами.
- Теорема: В равнобедренном треугольнике углы при основании равны.
- Признак: Если в треугольнике два угла равны, то он равнобедренный.
- Свойство медианы: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Материалы школы Юайти