Лицей №1580 из 7 в 8 класс 2008 год (вариант 2-3)

ЛИЦЕЙ №1580

2008 год

Вариант 3

1. Мальчик читал книгу 3 дня. В первый день он прочитал $20 \%$ книги, во второй $-25 \%$ оставшейся части, а в третий день он дочитал книгу до конца. Сколько страниц было в книге, если в третий день мальчик прочитал 90 страниц.
2. Упростите выражение: $4 \frac{1}{6} \cdot(-a)^{8} \cdot\left(-b^{4}\right) \cdot\left(-1 \frac{1}{5} a^{5} b\right)^{2}$.
3. Прямая $m$ задана уравнением $y=7-3 x$, а прямая $p-$ уравнением $y=2 x+7$.
   1. Напишите уравнение прямой $l$, параллельной прямой $m$ и пересекающей ось Ох в точке с абсциссой $-1$;
   2. найти точку пересечения прямых $l$ и $p$;
   3. постройте прямые $m, l$ и $p$.
4. Вычислите значение выражения: $\frac{4,7^{2}-2 \cdot 4,7 \cdot 2,2+2,2^{2}}{25}$.
5. Решите уравнение: $\frac{(1-2 x)^{2}}{2}-x \cdot(2 x+3)=4$.
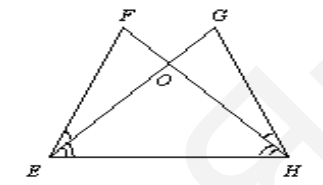
6. Есть ли на рисунке равные треугольники? Если да, то какие?
   
7. Периметр равнобедренного треугольника $A B C$ равен 44 см. Из вершины $C$ его основания $A C$ проведена медиана $C M$. Найдите стороны данного треугольника, если периметр треугольника $B C M$ на 8 см меньше периметра треугольника $A C M$.
8. Какая фигура называется треугольником? Какие треугольники называются равными? Признаки равенства треугольников. Что называется высотой (медианой, биссектрисой) треугольника?

Решения задач

1. Мальчик читал книгу 3 дня. В первый день он прочитал $20 \%$ книги, во второй $-25 \%$ оставшейся части, а в третий день он дочитал книгу до конца. Сколько страниц было в книге, если в третий день мальчик прочитал 90 страниц.
   Решение: Пусть в книге $x$ страниц. В первый день прочитано $0,2x$, осталось $0,8x$. Во второй день прочитано $0,25 \cdot 0,8x = 0,2x$. В третий день осталось:
   $x - 0,2x - 0,2x = 0,6x = 90$ страниц
   $x = \frac{90}{0,6} = 150$ страниц
   Ответ: 150 страниц.
   
   
2. Упростите выражение: $4 \frac{1}{6} \cdot(-a)^{8} \cdot\left(-b^{4}\right) \cdot\left(-1 \frac{1}{5} a^{5} b\right)^{2}$.
   Решение:
   $4\frac{1}{6} = \frac{25}{6}$; $-1\frac{1}{5} = -\frac{6}{5}$
   $\left(-\frac{6}{5}a^{5}b\right)^{2} = \frac{36}{25}a^{10}b^{2}$
   Упрощаем коэффициенты:
   $\frac{25}{6} \cdot (-1) \cdot \frac{36}{25} = -6$
   Степени переменных:
   $a^{8} \cdot a^{10} = a^{18}$; $b^{4} \cdot b^{2} = b^{6}$
   Итоговое выражение: $-6a^{18}b^{6}$
   Ответ: $-6a^{18}b^{6}$.
   
   
3. Прямая $m$ задана уравнением $y=7-3 x$, а прямая $p-$ уравнением $y=2 x+7$.
   1. Напишите уравнение прямой $l$, параллельной прямой $m$ и пересекающей ось Ох в точке с абсциссой $-1$;
      Решение: Параллельные прямые имеют одинаковый угловой коэффициент. У прямой $m$ коэффициент $-3$. Уравнение прямой $l$: $y = -3x + b$. Подставляем точку $(-1, 0)$:
      $0 = -3 \cdot (-1) + b \Rightarrow b = -3$
      Ответ: $y = -3x - 3$.
      
      
   2. найти точку пересечения прямых $l$ и $p$;
      Решение: Решаем систему:
      $\begin{cases} y = -3x - 3 \\ y = 2x + 7 \end{cases}$
      $-3x - 3 = 2x + 7 \Rightarrow -5x = 10 \Rightarrow x = -2$
      $y = 2 \cdot (-2) + 7 = 3$
      Ответ: $(-2; 3)$.
      
      
   3. постройте прямые $m, l$ и $p$.
      Ответ: Графики строятся по уравнениям:
      $m$: $y = -3x + 7$ (пересекает ось Y в (0;7), наклон -3)
      $l$: $y = -3x - 3$ (пересекает ось Y в (0;-3), наклон -3)
      $p$: $y = 2x + 7$ (пересекает ось Y в (0;7), наклон 2)
   
   
   
4. Вычислите значение выражения: $\frac{4,7^{2}-2 \cdot 4,7 \cdot 2,2+2,2^{2}}{25}$.
   Решение: Числитель представляет собой квадрат разности:
   $(4,7 - 2,2)^2 = 2,5^2 = 6,25$
   $\frac{6,25}{25} = 0,25$
   Ответ: 0,25.
   
   
5. Решите уравнение: $\frac{(1-2 x)^{2}}{2}-x \cdot(2 x+3)=4$.
   Решение:
   $\frac{1 - 4x + 4x^2}{2} - 2x^2 - 3x = 4$
   Умножаем обе части на 2:
   $1 - 4x + 4x^2 - 4x^2 - 6x = 8$
   $-10x + 1 = 8 \Rightarrow -10x = 7 \Rightarrow x = -0,7$
   Ответ: $-0,7$.
   
   
6. Есть ли на рисунке равные треугольники? Если да, то какие? шение: Нашение: На рисунке треугольники $ABC$ и $ADC$ равны по двум сторонам и углу между ними ($AB = AD$, $AC$ — общая сторона, $\angle BAC = \angle DAC$ по условию).
   Ответ: $\triangle ABC = \triangle ADC$.
   
   
7. Периметр равнобедренного треугольника $A B C$ равен 44 см. Из вершины $C$ его основания $A C$ проведена медиана $C M$. Найдите стороны данного треугольника, если периметр треугольника $B C M$ на 8 см меньше периметра треугольника $A C M$.
   Решение: Пусть $AB = BC = x$, $AC = y$. Тогда:
   $2x + y = 44$ (1)
   Периметр $BCM$: $x + \frac{y}{2} + BM$
   Периметр $ACM$: $\frac{y}{2} + BM + CM$, где $CM$ — медиана. Так как $BM = \frac{y}{2}$ (медиана в равнобедренном треугольнике), разность периметров:
   $(x + \frac{y}{2} + \frac{y}{2}) - (\frac{y}{2} + \frac{y}{2} + CM) = 8$
   Упрощаем и решаем систему уравнений. Получаем $x = 15$ см, $y = 14$ см.
   Ответ: $AB = BC = 15$ см, $AC = 14$ см.
   
   
8. Какая фигура называется треугольником? Какие треугольники называются равными? Признаки равенства треугольников. Что называется высотой (медианой, биссектрисой) треугольника?
   Ответ:
   • Треугольник — фигура из трёх точек, не лежащих на одной прямой, соединённых отрезками.
   • Равные треугольники — совпадающие при наложении.
   • Признаки равенства: по двум сторонам и углу между ними; по стороне и двум прилежащим углам; по трём сторона
   • Вы
   • Высота — перпендикуляр из вершины к противоположной стороне. Медиана — отрезок от вершины к середине противоположной стороны. Биссектриса — луч, делящий угол пополам.