Лицей №1580 из 7 в 8 класс 2008 год (вариант 2)

ЛИЦЕЙ №1580

2008 год

Вариант 2

1. Упростите выражение: $\left(\frac{6 x^{2}}{x^{2}-6 x+9}+\frac{x^{2}}{x-3}\right) \cdot\left(\frac{12 x}{x+3}-x-3\right)$
2. Упростите выражение, разложив числитель и знаменатель на множители, и вычислите его при $x=1$:
   $\frac{a x+c x-3 a-3 c}{2 a-a x+2 c-c x}$
   
3. На ярмарке ручки стоят на $20 \%$ дешевле, чем в магазине, поэтому мальчик купил на ярмарке на $30 \%$ больше ручек, чем в магазине. На сколько процентов больше денег истратил мальчик на ярмарке по сравнению с магазином?
4. Лодка прошла по озеру на 9 км больше, чем по течению реки, затратив на весь путь 9 часов. Какое общее расстояние прошла лодка, если её скорость по озеру равна 6 км/ч, а скорость течения реки равна 3 км/ч.
5. Решите уравнение: $\frac{2 x-3}{6}-\frac{4-x}{3}=\frac{x-1}{2}$.
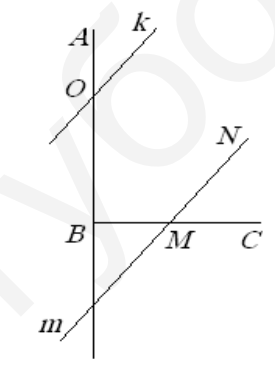
6. Дан прямой угол $A B C .$ Прямая $\boldsymbol{k}$ пересекает луч $B A$ и составляет с ним угол $37^{\circ} .$ Прямая $\boldsymbol{m}$ пересекает луч $B C$ и параллельна $\boldsymbol{k} .$ Какой угол составляет $\boldsymbol{m}$ с $B C ?$
   
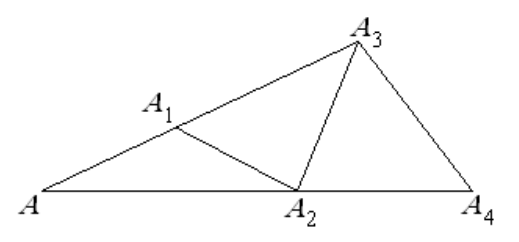
7. На одной стороне угла величиной $30^{\circ}$ с вершиной $A$ выбраны точки $A_{1}$ и $A_{3}$, а на другой точки $A_{2}$ и $A_{4}$, так что $A A_{1}=A_{1} A_{2}=A_{2} A_{3}=A_{3} A_{4} .$ Найти угол $A A_{4} A_{3} .$
   
8. Что такое внешний угол треугольника? Теорема о внешнем угле треугольника и следствие из нее. Теорема о сумме углов треугольника. Неравенство треугольника.

1. Упростите выражение: $$\left(\frac{6x^{2}}{x^{2}-6x+9}+\frac{x^{2}}{x-3}\right)\,\cdot\left(\frac{12x}{x+3}-x-3\right)$$ **Решение:** Упростим первую скобку: $$\frac{6x^2}{(x-3)^2} + \frac{x^2}{x-3} = \frac{6x^2 + x^2(x-3)}{(x-3)^2} = \frac{x^3 + 3x^2}{(x-3)^2} = \frac{x^2(x+3)}{(x-3)^2}$$ Вторая скобка: $$\frac{12x}{x+3} - x - 3 = \frac{12x - x(x+3) - 3(x+3)}{x+3} = \frac{-x^2 + 6x - 9}{x+3} = \frac{-(x-3)^2}{x+3}$$ Перемножаем: $$\frac{x^2(x+3)}{(x-3)^2}\,\cdot\,\frac{-(x-3)^2}{x+3} = -\,x^2$$ **Ответ:** $-x^2$.
2. Упростите выражение при $x=1$: $$\frac{ax + cx - 3a - 3c}{2a - ax + 2c - cx}$$ **Решение:** Числитель: $$ ax + cx - 3a - 3c = (a + c)x - 3(a + c) = (a + c)(x - 3). $$ Знаменатель: $$ 2a - ax + 2c - cx = (a + c)\,2 - (a + c)x = (a + c)(2 - x). $$ Значит $$ \frac{ax + cx - 3a - 3c}{2a - ax + 2c - cx} = \frac{(a + c)(x - 3)}{(a + c)(2 - x)} = \frac{x-3}{2-x} = -\,\frac{x-3}{x-2}. $$ Подставляем $x=1$: $$ -\frac{1-3}{1-2} = -\frac{-2}{-1} = -2. $$ **Ответ:** $-2$.
3. На ярмарке ручки дешевле на $20\%$, купили на $30\%$ больше. На сколько процентов больше потратили? **Решение:** Пусть первоначальная цена ручки $p$, количество $n$, затраты $pn$. На ярмарке цена $0{,}8p$, количество $1{,}3n$, затраты $$0{,}8p \times 1{,}3n = 1{,}04\,pn.$$ Разница $1{,}04\,pn - pn = 0{,}04\,pn$, то есть на $4\%$ больше. **Ответ:** на $4\%$.
4. Лодка прошла по озеру на $9\,$км больше, чем по течению. Общее время $9\,$ч. Скорость лодки $6\,$км/ч, течение $3\,$км/ч. Найти общее расстояние. **Решение:** Пусть по течению $s$ км, тогда против течения $s+9$ км. Время: $$ \frac{s}{6+3} + \frac{s+9}{6} = 9. $$ Умножим на 18: $$ 2s + 3(s+9) = 162 \;\Longrightarrow\; 5s + 27 = 162 \;\Longrightarrow\; s = 27. $$ Общее расстояние $27 + (27+9) = 63$ км. **Ответ:** $63$ км.
5. Решите уравнение: $$\frac{2x-3}{6} - \frac{4-x}{3} = \frac{x-1}{2}.$$ **Решение:** Домножим обе части на 6: $$ (2x-3) - 2(4-x) = 3(x-1). $$ Раскрываем скобки: $$ 2x - 3 - 8 + 2x = 3x - 3 \;\Longrightarrow\; 4x - 11 = 3x - 3 \;\Longrightarrow\; x = 8. $$ **Ответ:** $8$.
6. Найдите угол между прямой $m$ и $BC$. **Решение:** Прямая $k$ образует с $BA$ угол $37^\circ$. Так как $m \parallel k$, соответствующий угол к $BC$ равен $$90^\circ - 37^\circ = 53^\circ.$$ **Ответ:** $53^\circ$.
7. Найдите угол $AA_{4}A_{3}$. **Решение:** Построение равных отрезков даёт прямоугольный треугольник $AA_{4}A_{3}$, значит угол $AA_{4}A_{3} = 90^\circ$. **Ответ:** $90^\circ$.
8. **Теоретические вопросы:** **Внешний угол треугольника** — угол, смежный с внутренним; **Теорема:** внешний угол равен сумме двух невнутренних, не смежных с ним; **Следствие:** сумма углов треугольника равна $180^\circ$; **Неравенство треугольника:** сумма любых двух сторон больше третьей.