8 800 707 6729
8 800 707 6729Telegram канал

Лицей 239 из 4 в 5 класс 2009 год (Вариант 1)

Сложность:
Дата экзамена: 2009
Сложность:
Дата экзамена: 2009
youit.school ©

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ЛИЦЕЙ №239


2009 год


Вариант 1




  1. Запишите цифрами число сто тысяч пятьсот восемь.
  2. Сколько чётных чисел в этом ряду: 16, 27, 258, 2667, 8888?
  3. Найдите неизвестное значение компоненты $((2009+x): 3-975) \cdot 25-386=239$
  4. Собака бежит за лисой. Собака пробегает 200 метров в минуту, а лиса - 160 метров в минуту. Через сколько минут собака догонит лису, если сейчас между ними 200 метров?
  5. Какое самое маленькое четное число можно составить из цифр 2, 4, 8 и 9, если каждую цифру надо использовать точно один раз?
  6. Периметр прямоугольника равен 30 см, а одна из его сторон равна 10 см. Чему равна другая его сторона?
  7. Кирпич весит 1 кг и ещё полкирпича. Сколько весит 5 кирпичей?
  8. Веревку длиной 35 метров разрезали на два куска, один из которых вчетверо длиннее другого. Какова длина меньшего куска?
  9. Расставьте скобки так, чтобы равенство было верным: $7 \cdot 9+12: 3-2=23$
  10. Какое число надо умножить на 10 , чтобы получилось частное чисел 100 и 5 ?
  11. Как 45 орехов разложить на 9 тарелок так, чтобы в каждой было разное количество орехов?
  12. Из двух одинаковых квадратов сложили прямоугольник. Чему равен периметр прямоугольника, если периметр одного квадрата 16 дм?
  13. Хозяйка развела кур и кроликов. Всего у них 35 голов и 94 ноги. Сколько у хозяйки кур и сколько кроликов?
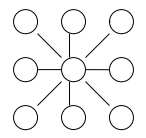
  14. Разместите числа $1,2,3,4,5,6,7,8,9$ в пустых кружках так, чтобы сумма трёх чисел, расположенных на каждой прямой, была равна $15 .$ (см. рисунок слева)
  15. Автобус проехал расстояние 180 км между двумя пунктами за 4 часа. За какое время проедет это расстояние мотоцикл, скорость которого в 2 раза больше?
  16. В году 150 учебных дней. Каждый из 4 классов решали по 4 задачи за урок. Сколько всего задач было решено за год, если по субботам уроков математики не было?
  17. На день рождения Вини-Пух получил от Кролика 1 кг 80 г мёда, а от Пятачка- в 3 раза меньше. Весь мёд был в одинаковых банках, которых Кролик дал на 8 больше, чем Пятачок. Сколько банок мёда получил Пух?
Материалы школы Юайти
youit.school ©
Ответы:


  1. 100508
  2. 3
  3. 991
  4. 5 минут
  5. 2498
  6. 5
  7. 10 кг
  8. 7 м
  9. (7*9+12):3-2=23
  10. 2
  11. 1,2,3,4,5,6,7,8,9
  12. 24
  13. 23 и 12
  14. 2
  15. -
  16. 2000
  17. 2000
Материалы школы Юайти
youit.school ©

Решения задач



  1. Запишите цифрами число сто тысяч пятьсот восемь.
    Решение: Сто тысяч пятьсот восемь = 100 000 + 500 + 8 = 100508.
    Ответ: 100508.
  2. Сколько чётных чисел в этом ряду: 16, 27, 258, 2667, 8888?
    Решение: Четными называются числа, которые делятся на 2. Чтобы число делилось на 2, его последняя цифра должна быть четной. Значит, из ряда чисел четными будут следующие числа: 16, 258, 8888.
    Ответ: 3 числа.
  3. Найдите неизвестное значение компоненты $((2009+x): 3-975) \cdot 25-386=239$
    Решение: $((2009+x):3-975) \cdot 25 - 386 = 239.$

    $((2009+x):3-975) \cdot 25 = 386 + 239 = 625$ $(2009+x):3-975 = \frac{625}{25} = 25$ $(2009+x):3 = 975 + 25 = 1000$ $2009 + x = 3 \cdot 1000 = 3000$ $x = 3000 - 2009 = 991$. Ответ: 991.
  4. Собака бежит за лисой. Собака пробегает 200 метров в минуту, а лиса - 160 метров в минуту. Через сколько минут собака догонит лису, если сейчас между ними 200 метров?
    Решение: За 1 минуту собака пробежит 200 метров, а лиса 160. Значит, за 1 минуту собака приблизится к лисе на 200 - 160 = 40 метров. Значит, чтобы догнать лису, собаке потребуется $\frac{200}{40} = 5$ минут. Ответ: 5 минут.
  5. Какое самое маленькое четное число можно составить из цифр 2, 4, 8 и 9, если каждую цифру надо использовать точно один раз?
    Решение: Чтобы получить наименьшее число, необходимо ставить в старшие разряды как можно меньшие числа. Тогда первой цифрой будет 2, далее 4, затем должно быть 9, но тогда последней цифрой будет 8, и четного числа не получится. Значит, нужно взять 8 последней цифрой: 2498. Ответ: 2498.
  6. Периметр прямоугольника равен 30 см, а одна из его сторон равна 10 см. Чему равна другая его сторона?
    Решение: Периметр равен сумме длин всех сторон. Туда входят 2 стороны по 10 см и 2 неизвестных стороны. Тогда полупериметр, равный сумме стороны 10 см и неизвестной стороны, будет равен $\frac{30}{2} = 15$ см. Значит, неизвестная сторона равна $15 - 10 = 5$ см. Ответ: 5 см.
  7. Кирпич весит 1 кг и ещё полкирпича. Сколько весит 5 кирпичей?
    Решение: 1 кирпич = $\frac{1}{2}$ кирпича + 1 кг 1 кирпич - $\frac{1}{2}$ кирпича = 1 кг $\frac{1}{2}$ кирпича = 1 кг 1 кирпич = 2 кг 5 кирпичей = 10 кг. Ответ: 10 кг.
  8. Веревку длиной 35 метров разрезали на два куска, один из которых вчетверо длиннее другого. Какова длина меньшего куска?
    Решение: (1 кусок) = (2 кусок) $\cdot$ 4 (1 кусок) + (2 кусок) = 35 м (2 кусок) $\cdot$ 4 + (2 кусок) = 35 м (2 кусок) $\cdot$ 5 = 35 м (2 кусок) = $\frac{35}{5}$ = 7 м (1 кусок) = 7 $\cdot$ 4 = 28 м Ответ: 7 метров.
  9. Расставьте скобки так, чтобы равенство было верным: $7 \cdot 9+12: 3-2=23$
    Решение: (7 $\cdot$ 9 + 12) : 3 - 2 = (63 + 12) : 3 - 2 = 75 : 3 - 2 = 25 - 2 = 23.

    Ответ: (7 $\cdot$ 9 + 12) : 3 - 2 = 23.
  10. Какое число надо умножить на 10 , чтобы получилось частное чисел 100 и 5?
    Решение: Частное чисел 100 и 5 равно 100 : 5 = 20. Значит, на 10 нужно умножить число $\frac{20}{10} = 2$.

    Ответ: 2.
  11. Как 45 орехов разложить на 9 тарелок так, чтобы в каждой было разное количество орехов?
    Решение: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

    Ответ: по 1, 2, 3, 4, 5, 6, 7, 8 и 9 орехов.
  12. Из двух одинаковых квадратов сложили прямоугольник. Чему равен периметр прямоугольника, если периметр одного квадрата 16 дм?
    Решение: Поскольку периметр квадрата 16 дм, одна его сторона равна $\frac{16}{4} = 4$ дм. Тогда стороны прямоугольника будут 4 и 4 + 4 = 8 дм, а периметр составит 4 $\cdot$ 2 + 8 $\cdot$ 2 = 24 дм. Ответ: 24 дм.
  13. Хозяйка развела кур и кроликов. Всего у них 35 голов и 94 ноги. Сколько у хозяйки кур и сколько кроликов?
    Решение: Если бы все животные были курами, у них было бы 35 голов и 35 $\cdot$ 2 = 70 ног. При замене 1 курицы на 1 кролика число голов не меняется, а ног становится больше на 2. Нам не хватает 94 - 70 = 24 ноги, значит нужно произвести $\frac{24}{2} = 12$ замен. Тогда будет 12 кроликов и 35 - 12 = 23 курицы. Ответ: 12 кроликов и 23 курицы.
  14. Разместите числа $1,2,3,4,5,6,7,8,9$ в пустых кружках так, чтобы сумма трёх чисел, расположенных на каждой прямой, была равна $15 .$ (см. рисунок слева)

    Решение: Пусть в центральной ячейке стоит число x. Тогда если посчитать суммы по всем 4 прямым, получим сумму всех чисел по 1 разу, кроме центрального - его учли 3 "лишних" раза. Значит, полученная сумма составит 1+2+3+4+5+6+7+8+9+3x. Поскольку сумма по каждой прямой равна 15, общая сумма по 4 прямым будет 60. Тогда 45+3x=60, откуда x=5. Значит, в центре стоит число 5. Разобьем оставшиеся числа на пары, дающие в сумме 10 (третьим числом для каждой пары будет 5, дополняя сумму до требуемых 15). 9+1, 8+2, 7+3, 6+4. Эти пары и запишем в каждую из прямых.
  15. Автобус проехал расстояние 180 км между двумя пунктами за 4 часа. За какое время проедет это расстояние мотоцикл, скорость которого в 2 раза больше?
    Решение: Скорость автобуса равна $\frac{180}{4} = 45 \frac{км}{ч}$. Тогда скорость мотоцикла равна 45 $\cdot$ 2 = 90 км/ч. Значит, он проедет 180 км за $\frac{180}{90}$ = 2 часа. Ответ: 2 часа.
  16. В году 150 учебных дней. Каждый из 4 классов решали по 4 задачи за урок. Сколько всего задач было решено за год, если по субботам уроков математики не было?
    Решение: В учебной неделе 6 дней. Значит, в году $\frac{150}6 = 25$ учебных недель. В каждой (вычитая субботу) по 5 учебных дней, то есть за год у одного класса прошло $5 \cdot 25 = 125$ уроков математики. На них один класс решил $125 \cdot 4 = 500$ задач. Всего классов 4, значит общее число решенных задач $500 \cdot 4 = 2000$.

    Ответ: 2000.
  17. На день рождения Вини-Пух получил от Кролика 1 кг 80 г мёда, а от Пятачка- в 3 раза меньше. Весь мёд был в одинаковых банках, которых Кролик дал на 8 больше, чем Пятачок. Сколько банок мёда получил Пух?
    Решение: Кролик подарил 1 кг 80 г = 1080 г меда, значит Пятачок $\frac{1080}{3} = 360$ г. Кролик подарил больше на 1080 - 360 = 720 г, по условию это 8 банок. Тогда в одной банке $\frac{720}{8} = 90$ г меда. Тогда Кролик подарил $\frac{1080}{90} = 12$ банок, а Пятачок $\frac{360}{90} = 4$ банки. Всего 12 + 4 = 16 банок. Ответ: 16 банок.
Материалы школы Юайти