СУНЦ УРФУ из 8 в 9 класс 2014 год

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2014 год

Вариант 1

Часть B К каждому заданию приведите только ответ

1. Найдите последнюю цифру числа $3^{2014}$.
2. Решите неравенство $1+x-2 x^{2}<0$.
3. Шариковая ручка стоит 15 рублей. Какое количество таких ручек можно купить на 400 рублей после повышения цены на $20 % ?$
4. Извлечь внешний корень $\sqrt{13-\sqrt{48}}$.
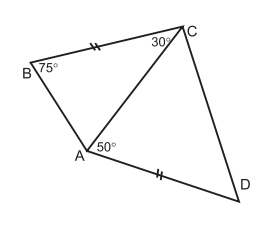
5. Найдите $\angle A D C$, если $B C=A D$ (рисунок).
   
6. Пусть $E$ и $F$ - середины сторон $B C$ и $A D$ параллелограмма $A B C D$. Найдите площадь четырехугольника, образованного прямыми $A E, E D, B F$ и $F C$, если известно, что площадь $A B C D$ равна 20.
7. Два рыбака поймали 80 рыб, причем $5 / 9$ улова первого составляли караси, а 7/11 улова второго - окуни. Сколько рыб поймал каждый из них?
8. Найдите сумму корней уравнения ||$|3-x|+3|-1|=4$.
9. Длины оснований трапеции равны 10 и 6 . Через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найдите длину отрезка этой прямой, заключенного между боковыми сторонами трапеции.
10. При каких значениях параметра $k$ уравнение $x^{2}-6|x|+9-k^{2}=0$ имеет ровно три корня?
    
    Часть C
    К заданиям нужно не только привести ответ, но и полностью оформить решение.
11. Решите уравнение $\frac{3}{x+2}-\frac{2 x-1}{x+1}=\frac{2 x+1}{x^{2}+3 x+2}$.
12. Упрости $\frac{a^{2}-4}{\sqrt{\left(\frac{a^{2}+4}{2 a}\right)^{2}-4}}$
13. Окружность, вписанная в ромб $A B C D$, касается сторон $A B$ и $B C$ в точках $M$ и $P$ соответственно, причем $M P=B P$. Найдите периметр ромба, если радиус окружности равен $\sqrt{3}$.
14. Для наполнения бассейна имеется 3 трубы. Первой трубе для наполнения бассейна требуется времени вдвое меньше, чем второй и на 4 часа больше, чем третьей. Три трубы наполнили бы бассейн за 4 часа, но, по техническим требованиям, одновременно могут работать только две. Найдите минимальное время наполнения бассейна.

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2014 год

Вариант 1

Часть B К каждому заданию приведите только ответ

1. $9 .$
   
2. $x1$.
   
3. 22
   
4. $\sqrt{12}-1$.
   
5. $65^{\circ}$.
   
6. $5 .$
   
7. 36 и $44 .$
   
8. $6 .$
   
9. 7,5.
   
10. $k=\pm 3$.
    
    Часть C
    
11. $x=1$.
    
12. $-2 a$.
    
13. 16.
    
14. 4,8 часа.
    

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2014 год

Вариант 1

Часть B К каждому заданию приведите только ответ

1. $3^{2014}=9^{1007}=81^{503} \cdot 9$.
2. $y=1+x-2 x^{2}-$ квадратичная функция, графиком которой является парабола с ветвями, направленными вниз. Значит отрицательные значения это функция принимает в точках слева от меньшего корня и справа от большегO.
3. Стоимость ручки после повышения цены на $20 \%$ равна 18 рублей.
4. $\sqrt{13-\sqrt{48}}=\sqrt{1-2 \sqrt{12}+12}=$ $=\sqrt{(1-\sqrt{12})^{2}}=|1-\sqrt{12}|=\sqrt{12}-1 .$
5. $\angle B A C=75^{\circ}$, поэтому оба треугольника - равнобедренные.
6. Сумма площадей треугольников $A B E$ и $D C E$ равна половине площади параллелограмма. В оставшемся треугольнике $A E D$ площади 10 прямые $F B$ и $F C$ являются средними линиями, поэтому отсекают треугольники площади которых равны четверти площади треугольника $A E D .$
7. Количество рыб, пойманных первым рабаком кратно 9, а вторым 11. Поэтому можно записать равенство $9 x+11 y=80$, где $x$ и $y$ - некоторые целые неотрицательные числа. Переменная $y$ может принимать лишь восемь заничений $(0,1,2,3,4,5,6,7)$. Только при $y=4$ получаем целое $x$.
8. Так как выражение $|3-x|+3$ всегда положительно, то || $3-x|+3|=$ $=|3-x|+3 .$ Поэтому уравнение равносильно следующему: || $3-x|+2|=4 .$ Аналогично рассуждая, получаем уравнение $|3-x|=2$, которое имеет два корня: 1 и $5 .$
9. Диагонали трапеции делятся точкой пересечения в отношении, равном отношению оснований. По теореме Фалеса в том же отношении делятся боковые стороны прямой, параллельной основаниям и проходящей через пересечение диагоналей. В нашей задаче это отношение равно $5: 3 .$ Используя подобие треугольников, получаем, что искомый отрезок делится точкой перечечения пополам, а каждая из половин равна $7 / 4$.
10. Заменим переменную: $t=|x|$, тогда получим квадратное уравнение $t^{2}-6 t+9-k^{2}=0$. Чтобы исходное уравнение имело три корня, у нового уравнения должен быть корень $t=0$. Такое возможно только при $9-k^{2}=0$. Стоит заметить, что в этом случае второй корень уравнения равен 6 , а значит исходное уравнение будет иметь три корня, а не один.
    
    Часть C
    
11. Так как знаменатели дробей не могут обращаться в ноль, поэтому $x \neq-1, x \neq-2 .$
    Домножив уравнение на общий знаменатель всех дробей $((x+1)(x+2))$ и приведя подобные, получим $2 x^{2}+2 x-4=0$. Корни этого уравнения $x=1$ и $x=-2$, но второй корень посторонний (знаменатель обращается в ноль).
12. $\frac{a^{2}-4}{\sqrt{\left(\frac{a^{2}+4}{2 a}\right)^{2}-4}}=\frac{a^{2}-4}{\sqrt{\frac{a^{4}-4 a^{2}+4}{(2 a)^{2}}}}=\frac{\left(a^{2}-4\right)|2 a|}{\sqrt{\left(a^{2}-4\right)^{2}}}=\frac{\left(a^{2}-4\right)|2 a|}{\left|a^{2}-4\right|} .$
    При $a<-2$ модуль в числителе раскрывается со знаком $-$, а модуль в знаменателе - со знаком $+.$
13. Так как отрезки касательных, проведенных из одной точки к одной окружности равны, то $B M=B P$. Учитывая условие $M P=B P$, получаем, что треугольник $B M P$ - равносторонний, то есть острый угол ромба равен $60^{\circ}$.
    Высота $A H$ ромба, проведенная из вершины $A$ к стороне $B C$ равна двум радиусам вписанной окружности. Из прямоугольного треугольника $B A H$ находим: $A B=A H / \cos 60^{\circ}=4$.
    Периметр ромба равен $4 A B=16$.
14. Пусть $x-$ время наполения бассейна первой трубой. Тогда $2 x-$ время наполнения бассейна второй трубой, $x-4$ - время напонения бассейна третьей трубой. Сразу же заметим, что $x>4$.
    Так как три трубы наполнили бы бассейн за 4 часа, то $$ 4(1 / x+1 /(2 x)+1 /(x-4))=1 $$ Решая это уравнение, получаем два корня: $x=2$ и $x=12$. Но по смыслу задачи $(x>4)$ подходит только второй. \\ Чтобы бассейн наполнился за минимальное время двумя трубами, надо отключить самую медленнонаполняющую (это, конечно, вторая труба с временем наполнения бассейна 24 часа). Время наполнения бассейна двумя трубами (первой и второй) равно $1 /(1 / x+1 /(x-4))=1 /(1 / 12+1 / 8)=4,8$ часа.