СУНЦ УРФУ из 8 в 9 класс 2014 год

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2014 год

Вариант 2

Часть В
К каждому заданию приведите только ответ.

1. Решите неравенство: $\frac{x-2}{x^{2}}<0$.
   
2. Стирательная резинка стоит 16 рублей. Какое количество таких стирательных резинок можно купить на 250 рублей после понижения цены на $25 \%$.
   
3. Найдите последнюю цифру числа $2^{2014} .$
   
4. Упростите: $\sqrt{12-2 \sqrt{11}}$.
   
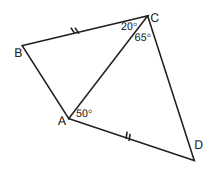
5. Найдите $\angle B A C$, если $B C=A D$, $\angle D C A=65^{\circ}, \angle B C A=20^{\circ}, \angle C A D=50^{\circ}$, (см. рисунок).
   
   
6. Известно, что $x_{1}$ и $x_{2}-$ корни уравнения $x^{2}-7 x+6=0 .$ Найдите $\frac{1}{x_{1}}+\frac{1}{x_{2}} .$
   
7. В параллелограмме $A B C D$ известны длины сторон: $A B=5$ и $B C=10 .$ Точка $K$ является пересечением биссектрисы угла $A B C$ с прямой $A D$. Найдите длину отрезка $B O$, если известно, что $O$ - точка пересечения $B K$ с диагональю $A C$ и $B K=6$.
   
8. Сколько точек пересечения у графиков функций $y=\left|x^{2}-4 x+3\right|$ и $y=5 ?$
   
9. В треугольнике $A B C$ сторона $A B=4, \angle A B C=135^{\circ}$. Найдите длину высоты, проведенной к стороне $B C$.
   
   
   Часть С
   К заданиям нужно не только привести ответ, но и полностью оформить решение.
10. Решите уравнение $\frac{3}{x-1}-\frac{2 x-7}{x-2}=\frac{2 x-5}{x^{2}-3 x+2}$.
    
11. В числе $\overline{64 X 5 Y}$ найдите цифры $X$ и $Y$, если известно, что это число делится на 36.
    
12. Окружность с центром $O$, вписанная в ромб $K L M N$, касается сторон $K L$ и $K N$ в точках $X$ и $Y$ соответственно, причем $\angle X O Y=135^{\circ}$. Найдите радиус окружности, если периметр ромба равен $8 \sqrt{2}$.
    
13. Найдите все значения параметра $a$, при которых уравнение $a x^{2}+12 x+4 a=0$ имеет единственное решение.
    

Решения задач

1. Ответ: $x \in (-\infty; 0) \cup (0; 2)$.
2. Ответ: 20.
3. Ответ: 4.
4. Ответ: $\sqrt{11} - 1$.
5. Ответ: $70^{\circ}$.
6. Ответ: $\frac{7}{6}$.
7. Ответ: 4.
8. Ответ: 2 точки.
9. Ответ: $2\sqrt{2}$.
10. Ответ: $x = 4$.
11. Ответ: $(X=1, Y=2)$ или $(X=6, Y=6)$.
12. Ответ: 1.
13. Ответ: $a = -3, 0, 3$.

Решения задач

1. Решите неравенство: $\frac{x-2}{x^{2}}<0$.
   Решение: Дробь отрицательна, когда числитель и знаменатель разных знаков. Знаменатель $x^2 > 0$ при $x \neq 0$. Тогда числитель $x - 2 < 0 \Rightarrow x < 2$. Учитывая $x \neq 0$, получаем $x \in (-\infty; 0) \cup (0; 2)$.
   Ответ: $x \in (-\infty; 0) \cup (0; 2)$.
2. Стирательная резинка стоит 16 рублей. Какое количество таких стирательных резинок можно купить на 250 рублей после понижения цены на $25 \%$.
   Решение: Новая цена резинки: $16 \cdot 0,75 = 12$ руб. Количество: $\frac{250}{12} \approx 20,83$. Целое число резинок: 20.
   Ответ: 20.
3. Найдите последнюю цифру числа $2^{2014}$.
   Решение: Последние цифры степеней 2 цикличны с периодом 4: $2, 4, 8, 6$. Остаток от деления 2014 на 4: $2014 = 4 \cdot 503 + 2$. Последняя цифра соответствует второй позиции цикла — 4.
   Ответ: 4.
4. Упростите: $\sqrt{12-2 \sqrt{11}}$.
   Решение: Представим подкоренное выражение как квадрат разности: $\sqrt{(\sqrt{11} - 1)^2} = \sqrt{11} - 1$.
   Ответ: $\sqrt{11} - 1$.
5. Найдите $\angle B A C$, если $B C=A D$, $\angle D C A=65^{\circ}, \angle B C A=20^{\circ}, \angle C A D=50^{\circ}$.
   Решение: Рассмотрим треугольники $ABC$ и $ADC$. Угол $\angle BAC = \angle CAD + \angle BCA = 50^{\circ} + 20^{\circ} = 70^{\circ}$.
   Ответ: $70^{\circ}$.
6. Известно, что $x_{1}$ и $x_{2}-$ корни уравнения $x^{2}-7 x+6=0$. Найдите $\frac{1}{x_{1}}+\frac{1}{x_{2}}$.
   Решение: По теореме Виета: $x_1 + x_2 = 7$, $x_1 \cdot x_2 = 6$. Тогда $\frac{1}{x_1} + \frac{1}{x_2} = \frac{x_1 + x_2}{x_1 x_2} = \frac{7}{6}$.
   Ответ: $\frac{7}{6}$.
7. В параллелограмме $A B C D$ известны длины сторон: $A B=5$ и $B C=10$. Точка $K$ является пересечением биссектрисы угла $A B C$ с прямой $A D$. Найдите длину отрезка $B O$, если известно, что $O$ - точка пересечения $B K$ с диагональю $A C$ и $B K=6$.
   Решение: Используя теорему Менелая для треугольника $ABD$ и секущей $BK$, получаем соотношение $\frac{BO}{OK} = \frac{2}{1}$. Тогда $BO = \frac{2}{3} BK = \frac{2}{3} \cdot 6 = 4$.
   Ответ: 4.
8. Сколько точек пересечения у графиков функций $y=\left|x^{2}-4 x+3\right|$ и $y=5$?
   Решение: Решаем уравнение $|x^2 - 4x + 3| = 5$. Рассмотрим два случая:
   • $x^2 - 4x + 3 = 5 \Rightarrow x^2 - 4x - 2 = 0$, корни $x = 2 \pm \sqrt{6}$ (2 точки).
   • $x^2 - 4x + 3 = -5 \Rightarrow x^2 - 4x + 8 = 0$, дискриминант отрицателен.
   Ответ: 2 точки.
9. В треугольнике $A B C$ сторона $A B=4$, $\angle A B C=135^{\circ}$. Найдите длину высоты, проведенной к стороне $B C$.
   Решение: Площадь треугольника $S = \frac{1}{2} AB \cdot BC \cdot \sin(135^{\circ}) = \frac{1}{2} \cdot 4 \cdot BC \cdot \frac{\sqrt{2}}{2}$. Выразим высоту $h$ из $S = \frac{1}{2} BC \cdot h$. Получим $h = 2\sqrt{2}$.
   Ответ: $2\sqrt{2}$.
10. Решите уравнение $\frac{3}{x-1}-\frac{2 x-7}{x-2}=\frac{2 x-5}{x^{2}-3 x+2}$.
    Решение: Общий знаменатель $(x-1)(x-2)$. Умножаем обе части на знаменатель: \[ 3(x-2) - (2x-7)(x-1) = 2x-5 \] Раскрываем скобки и упрощаем: \[ 3x - 6 - 2x^2 + 9x - 7 = 2x - 5 \Rightarrow -2x^2 + 10x - 13 = 2x - 5 \Rightarrow -2x^2 + 8x - 8 = 0 \] Решаем квадратное уравнение: $x = 2$ (не входит в ОДЗ) и $x = 4$.
    Ответ: $x = 4$.
11. В числе $\overline{64 X 5 Y}$ найдите цифры $X$ и $Y$, если известно, что это число делится на 36.
    Решение: Число делится на 36, если делится на 4 и 9. Условие на 4: $5Y$ делится на 4 → $Y = 2$ или $6$. Условие на 9: сумма цифр $6 + 4 + X + 5 + Y$ делится на 9.
    • При $Y = 2$: $15 + X + 2 = 17 + X$ → $X = 1$.
    • При $Y = 6$: $15 + X + 6 = 21 + X$ → $X = 6$.
    Ответ: $(X=1, Y=2)$ или $(X=6, Y=6)$.
12. Окружность с центром $O$, вписанная в ромб $K L M N$, касается сторон $K L$ и $K N$ в точках $X$ и $Y$ соответственно, причем $\angle X O Y=135^{\circ}$. Найдите радиус окружности, если периметр ромба равен $8 \sqrt{2}$.
    Решение: Сторона ромба $2\sqrt{2}$. Угол между радиусами $135^{\circ}$ соответствует углу ромба $135^{\circ}$. Радиус вписанной окружности $r = \frac{\text{площадь}}{\text{полупериметр}} = \frac{2\sqrt{2} \cdot 2\sqrt{2} \cdot \sin(135^{\circ})}{4\sqrt{2}} = 1$.
    Ответ: 1.
13. Найдите все значения параметра $a$, при которых уравнение $a x^{2}+12 x+4 a=0$ имеет единственное решение.
    Решение: Уравнение имеет единственное решение, если:
    • $a = 0$: уравнение становится линейным $12x = 0$ → одно решение.
    • $a \neq 0$: дискриминант $D = 144 - 16a^2 = 0$ → $a = \pm 3$.
    Ответ: $a = -3, 0, 3$.