СУНЦ УРФУ из 8 в 9 класс 2014 год

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2014 год

Вариант 1

Часть В К каждому заданию приведите только ответ

1. Решите неравенство: $\frac{x+1}{x^{2}}>0$.
2. Шариковая ручка стоит 15 рублей. Какое количество таких ручек можно купить на 400 рублей после повышения цены на $20 \%$.
3. Найдите последнюю цифру числа $3^{2014} .$
4. Упростите: $\sqrt{13-4 \sqrt{3}}$.
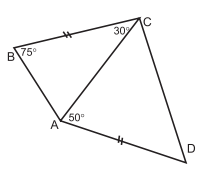
5. Найдите $\angle A D C$, если $B C=A D$, $\angle C B A=75^{\circ}, \angle B C A=30^{\circ}, \angle C A D=50^{\circ}$, (см. рисунок).
   
6. Известно, что $x_{1}$ и $x_{2}-$ корни уравнения $x^{2}+5 x+3=0 .$ Найдите $\frac{1}{x_{1}}+\frac{1}{x_{2}} .$
7. В параллелограмме $A B C D$ известно, что $A B=3$ и $B C=6 .$ Точка $K$ является пересечением биссектрисы угла $A B C$ с прямой $A D$. Найдите длину отрезка $B K$, если известно, что $B K$ пересекает диагональ $A C$ в точке $O$ и $B O=2$.
8. Сколько точек пересечения у графиков функций $y=\left|x^{2}-6 x+5\right|$ и $y=3 ?$
9. В треугольнике $A B C$ сторона $A B=6, \angle A B C=120^{\circ} .$ Найдите длину высоты, проведенной к стороне $B C .$
   
   Часть С
   К заданиям нужно не только привести ответ, но и полностью оформить решение.
10. Решите уравнение $\frac{3}{x+2}-\frac{2 x-1}{x+1}=\frac{2 x+1}{x^{2}+3 x+2}$.
11. В числе $\overline{42 X 4 Y}$ найдите цифры $X$ и $Y$, если известно, что это число делится на 72.
    
12. Окружность, вписанная в ромб $A B C D$, касается сторон $A B$ и $B C$ в точках $M$ и $P$ соответственно, причем $M P=B P$. Найдите периметр ромба, если радиус окружности равен $\sqrt{3}$.
    
13. Найдите все значения параметра $a$, при которых уравнение $a x^{2}+8 x+4 a=0$ имеет единственное решение.

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2014 год

Вариант 1

Часть В К каждому заданию приведите только ответ

1. $(-1 ; 0) \cup(0 ;+\infty)$.
   
   
2. 22.
3. $9 .$
4. $2 \sqrt{3}-1$.
5. $65^{\circ}$
6. $-\frac{5}{3}$.
7. $3 .$
8. $4 .$
9. $3 \sqrt{3}$.
   
   Часть С
   
10. $x=1$
11. $X=8, Y=0$ или $X=0$ и $Y=8$.
12. $16.$$
13. $-2 ; 0 ; 2 .$

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2014 год

Вариант 1

Часть В К каждому заданию приведите только ответ

1. Выражение $x^{2}-$ всегда неотрицательно и, так как стоит в знаменателе, отлично от нуля. Значит, $\frac{x+1}{x^{2}}>0 \Leftrightarrow x+1>0$ и $x \neq 0$.
2. Стоимость ручки после повышения равна $15+15 \cdot 0,2=18$ рублей. Заметим, что $400=22 \cdot 18+4$.
3. $3^{2014}=9^{1007}=81^{503} \cdot 9$.
4. $\sqrt{13-4 \sqrt{3}}=\sqrt{1-2 \cdot 2 \sqrt{3}+12}=\sqrt{(1-2 \sqrt{3})^{2}}=$ $=|1-2 \sqrt{3}|=2 \sqrt{3}-1 .$
5. $\angle B A C=180^{\circ}-75^{\circ}-30^{\circ}=75^{\circ}$. Получили, что $B C=A C=A D$. Тогда $\triangle A C D-$ равнобедренный и $\angle A C D=\angle A D C=\left(180^{\circ}-50^{\circ}\right) / 2=65^{\circ} .$
6. По теореме Виета $x_{1}+x_{2}=-5$ и $x_{1} \cdot x_{2}=3$. $\frac{1}{x_{1}}+\frac{1}{x_{2}}=\frac{x_{1}+x_{2}}{x_{1} \cdot x_{2}}=-\frac{5}{3}$.
7. Прямые $B C$ и $A D$ параллельны, $B K$ - секущая, тогда $\angle C B K=$ $=\angle B K A .$ По условию, $B K$ - биссектриса, значит $\angle C B K=\angle A B K .$ Получаем, что $\triangle A B K$ - равнобедренный и $A B=A K=3 .$ Треугольники $A O K$ и $B O C$ подобны и $O K: B O=A K: B C=1: 2$. Тогда $O K=1, B K=$ $=O K+O B=3 .$
8. $\left|x^{2}-6 x+5\right|=3 .$ Значит $x^{2}-6 x+5=3$ или $x^{2}-6 x+5=3 .$ Каждое из уравнеий имеет по два корня, значит у графиков функций всего 4 точки пересечения.
9. Пусть $A H-$ искомая высота. Так как треугольник $A B C$ тупоугольный, то $A H-$ вне треугольника. Тогда $\triangle A H B$ прямоугольный с углом $60^{\circ} .$ Окончательно $A H=A B \cdot \sin 60^{\circ}=3 \sqrt{3} .$
   
   Часть С
   К заданиям нужно не только привести ответ, но и полностью оформить
10. Знаменатели дробей не могут обращаться в ноль, поэтому $x \neq-1$, $x \neq-2 .$ Домножив уравнение на общий знаменатель всех дробей $(x+1)(x+2)$ и приведя подобные, получим $2 x^{2}+2 x-4=0$. Корни этого уравнения $x=1$ и $x=-2$, но второй корень посторонний (знаменатель обращается в ноль).
11. Число делится на 72, следовательно делится на 9 и на $8 .$ Тогда число $\overline{X 4 Y}$ делится на 8, значит и на $4 .$ Это воможно при $Y=0, Y=4$, $Y=8$. Сумма всех цифр $10+X+Y$ делится на 9.
    Получаем:
    если $Y=0$, то $X=8$;
    если $Y=8$, то $X=0$;
    если $Y=4$, то $X=4$.
    Последняя пара не подходит, так как число $\overline{X 4 Y}=444$ не делится на $8 .$
12. Так как отрезки касательных, проведенных из одной точки к одной окружности равны, то $B M=B P$. Учитывая условие $M P=B P$, получаем, что треугольник $B M P$ равносторонний, то есть острый угол ромба равен $60^{\circ}$. Высота $A H$ ромба, проведенная из вершины $A$ к стороне $B C$ равна двум радиусам вписанной окружности. Из прямоугольного треугольника $B A H$ находим: $A B=A H / \cos 60^{\circ}=4$. Периметр ромба равен $4 A B=16$.
13. При $a=0$ уравнение обращается в линейное, решение которого $x=0$. При $a \neq 0$ уравнение является квадратным и имеет одно решение, если дискриминант равен нулю. $D=64-16 a^{2}=0, a^{2}=4, a=\pm 2 .$