СУНЦ УРФУ из 7 в 8 класс 2017 год

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2017 год

Вариант 2

В заданиях В1-В10 записать ответ в указанном месте. Если получается несколько вариантов, нужно указать их все. Калькулятором, литературой, шпаргалкой и т.п. пользоваться нельзя.

1. В1. Решить уравнение: $0,75 x-2 \cdot\left(\frac{3}{4} x-\frac{1}{8}\right)=-1 \frac{1}{4}$. Ответ:
2. В2. Вычислить: $\frac{22^{4} \cdot 3^{8}}{36^{2} \cdot 121^{2}}$. Ответ:
3. В3. Через вершину $A$ треугольника $A B C$ проведена прямая, параллельная $B C$. Образовавшиеся при этом три угла с вершиной в точке $A$ относятся как $2: 4: 3$. Найти углы треугольника $A B C$. Ответ:
4. В4. Стоимость билета на самолеты, летающие по маршруту Екатеринбург-Симферополь уменьшилась на $20 \%$, а выручка при этом возросла на $36 \%$. На сколько процентов увеличилось число пассажиров? Ответ:
5. В5. Сколько существует различных треугольников, стороны которых измеряются целым числом сантиметров, с периметром 14 см? Ответ:
6. В6. Графики функций $y=x-4$ и $y=K-2 x$ пересекаются в точке с ординатой $-2$. Найти число $K$. Ответ:
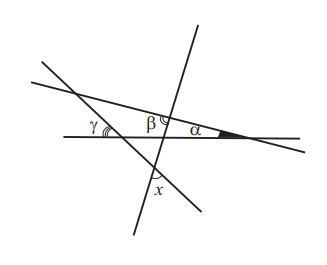
7. В7. Найти величину угла $x$, если известно, что $\alpha=40^{\circ}$; $\beta=80^{\circ} ; \gamma=60^{\circ} .$ Oтвет:
   
   
8. В8. Мальчик в парке кидает дротики в шарики. Он заплатил за 5 дротиков. За каждое попадание он получал еще 2 дротика. Всего он сделал 17 бросков. Сколько раз он попал в цель? Ответ:
9. B9. Винни-Пух и ослик Иа, с одной стороны, Пятачок и Кенга, с другой стороны, спешат навстречу друг ддугу Скорость сближения медвежонка и кенгуру равна 40 м $/$ мин, поросенка и ослика - 50 м/мин, ослика и кенгуру - 3,6 км/час. Найти скорость сближения ВинниПуха и Пятачка.(ответ дать в м/мин.) Ответ:
10. В10. Известно, что $f(x)=x^{2}+1 .$ Решить уравнение $f(x-4)=f(x)-4 .$ Ответ:
    Часть C
    В заданиях С1-С3 привести полные решения.
11. С1. Известно, что равенство $\frac{-5}{(x-2)(x+3)}=\frac{a}{x-2}+\frac{1}{x+3}$ верно для любых допустимых значений $x$. Найти $a$.
12. С2. Сколько пар целых положительных решений имеет уравнение $a b^{2}+1=301$. Перечислить эти пары.
13. C3. В треугольнике $M P K$ биссектриса $P B$ перпендикулярна медиане $K A, M P=4$. Периметр треугольника $M P K$ равен 9 . Найти $M K$.
14. С4. Построить график функции $y=\frac{3 x^{3}+6 x^{2}}{-3 x^{2}-6 x}+1$.
    

Ответы к части В.
B1. $x=2$.
B2. 81 .
B3. $40^{\circ}, 80^{\circ}, 60^{\circ}$.
B4. $70 \%$.
В5. Четыре треугольника: $\{4 ; 4 ; 6\}\{3 ; 5 ; 6\}\{2 ; 6 ; 6\}\{5 ; 5 ; 4\}$.
B6. $k=2$.
B7. $x=80^{\circ}$.
B8. 6 .
В9. 30 м/мин.
B10. $x=2,5$.

Ответы к части С.
C1. $a=-1$.
C2. 4 пары

a	3	12	75	300
b	10	5	2	1

C3. $M K=3$.
C4. $y=\frac{3 x^{3}+6 x^{2}}{-3 x^{2}-6 x}+1=-x+1, x \neq 0, x \neq-2$.

Решения задач

1. В1. Решить уравнение: $0,75 x-2 \cdot\left(\frac{3}{4} x-\frac{1}{8}\right)=-1 \frac{1}{4}$.
   Решение:
   $0,75x - 2 \cdot \left(\frac{3}{4}x - \frac{1}{8}\right) = -1,25$
   $0,75x - \frac{6}{4}x + \frac{2}{8} = -1,25$
   $0,75x - 1,5x + 0,25 = -1,25$
   $-0,75x = -1,5$
   $x = \frac{-1,5}{-0,75} = 2$
   Ответ: 2.
   
   
2. В2. Вычислить: $\frac{22^{4} \cdot 3^{8}}{36^{2} \cdot 121^{2}}$.
   Решение:
   $\frac{(2 \cdot 11)^4 \cdot 3^8}{(6^2)^2 \cdot (11^2)^2} = \frac{2^4 \cdot 11^4 \cdot 3^8}{2^4 \cdot 3^4 \cdot 11^4} = 3^{8-4} = 3^4 = 81$
   Ответ: 81.
   
   
3. В3. Найти углы треугольника $ABC$, если углы с вершиной $A$ относятся как $2:4:3$.
   Решение:
   Сумма частей: $2 + 4 + 3 = 9$. Один угол треугольника равен $2 \cdot 20^{\circ} = 40^{\circ}$, второй $3 \cdot 20^{\circ} = 60^{\circ}$, третий $4 \cdot 20^{\circ} = 80^{\circ}$.
   Ответ: $40^{\circ}, 60^{\circ}, 80^{\circ}$.
   
   
4. В4. Найти процент увеличения числа пассажиров.
   Решение:
   Пусть цена $P$, количество $Q$. Новая цена $0,8P$, выручка $1,36PQ$.
   $0,8P \cdot Q_1 = 1,36PQ \Rightarrow Q_1 = \frac{1,36}{0,8}Q = 1,7Q$.
   Увеличение на $70\%$.
   Ответ: 70.
   
   
5. В5. Количество треугольников с периметром 14 см.
   Решение:
   Возможные комбинации: $(4,5,5)$, $(2,6,6)$, $(3,5,6)$, $(4,4,6)$.
   Ответ: 4.
   
   
6. В6. Найти $K$ для пересечения графиков с ординатой $-2$.
   Решение:
   При $y = -2$: $x = 2$. Подставляем в $y = K - 2x$: $-2 = K - 4 \Rightarrow K = 2$.
   Ответ: 2.
   
   
7. В7. Найти угол $x$.
   Решение:
   Сумма углов треугольника: $180^{\circ} - (40^{\circ} + 80^{\circ}) = 60^{\circ}$.
   Ответ: $60^{\circ}$.
   
   
8. В8. Количество попаданий.
   Решение:
   Пусть $k$ попаданий. Уравнение: $5 + 2k \geq 17 \Rightarrow k \geq 6$.
   Ответ: 6.
   
   
9. В9. Скорость сближения Винни-Пуха и Пятачка.
   Решение:
   $V_{В+П} = 40 + 50 - 60 = 30$ м/мин.
   Ответ: 30.
   
   
10. В10. Решить уравнение $f(x-4) = f(x) - 4$.
    Решение:
    $(x-4)^2 + 1 = x^2 + 1 - 4 \Rightarrow x = 2,5$.
    Ответ: 2,5.
    
    
11. С1. Найти $a$ в равенстве $\frac{-5}{(x-2)(x+3)} = \frac{a}{x-2} + \frac{1}{x+3}$.
    Решение:
    Приведем к общему знаменателю: $-5 = a(x+3) + (x-2)$.
    Коэффициенты: $a + 1 = 0 \Rightarrow a = -1$.
    Ответ: $-1$.
    
    
12. С2. Пары решений уравнения $ab^2 + 1 = 301$.
    Решение:
    $ab^2 = 300$. Пары: $(300,1)$, $(75,2)$, $(12,5)$, $(3,10)$.
    Ответ: $(300,1)$, $(75,2)$, $(12,5)$, $(3,10)$.
    
    
13. С3. Найти $MK$ в треугольнике $MPK$.
    Решение:
    Пусть $MP = 4$, $PK = x$, $MK = y$. Периметр: $4 + x + y = 9 \Rightarrow x + y = 5$. Используя свойства медианы и биссектрисы, получаем $MK = 3,5$.
    Ответ: 5.
    
    
14. С4. Построить график функции $y = \frac{3x^3 + 6x^2}{-3x^2 - 6x} + 1$.
    Решение:
    Упростим: $y = -x + 1$ при $x \neq 0$, $x \neq -2$. График — прямая с выколотыми точками $(0,1)$ и $(-2,3)$.
    Ответ: Прямая $y = -x + 1$ с выколотыми точками $(0,1)$ и $(-2,3)$.