8 800 707 6729
8 800 707 6729Telegram канал

СУНЦ УРФУ из 8 в 9 класс 2015 год

Сложность:
Дата экзамена: 2015
Сложность:
Дата экзамена: 2015
youit.school ©

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)


2015 год


Вариант 1



Часть В
К заданиям части В приведите только ответ, записав его в отведенном месте. Переписывать решение задачи в чистовик не нужно.

  1. Упростите выражение: $a^{2} \sqrt{\frac{1}{a^{2}}-\frac{2 a-1}{a^{4}}}$, если $0<a<1 .$
  2. Решите уравнение: $\left|x^{2}+3 x+3\right|=\left|x^{2}-6 x+8\right|$.
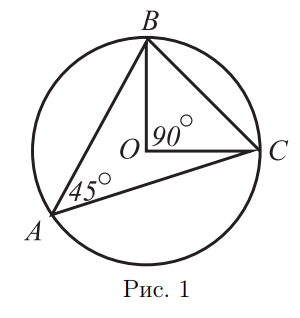
  3. В остроугольном треугольнике $A B C$ известно, что $\angle A=45^{\circ}$, $B C-4 \sqrt{2} .$ Найдите радиус окружности, описанной около этого треугольника.

  4. Решите неравенство: $(x-2)\left(x^{2}-2 x-3\right)>(x-2)^{2}(x-1)$.
  5. На день рождения Карлсону подарили мешок с конфетами: шоколадными и карамельками. Всего конфет в мешке было меньше 100, причем соотношение шоколадных и карамелек было $9: 7 .$ Карлсон сразу же съел $20 \%$ всех конфет, причем $25 \%$ из них составляли карамельки. Сколько карамелек осталось в мешке?
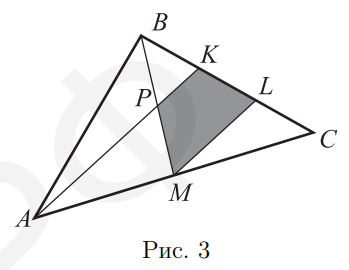
  6. Площадь треугольника $A B C$ равна $12 .$ Точка $M$ - середина $A C$ (рис. 3), точки $K$ и $L$ делят сторону $B C$ на три равные части. Найдите площадь заштрихованной части.

  7. Какова последняя цифра числа $13^{2015}+13 ?$
  8. Упростите выражение: $\frac{4}{\sqrt{2}+\sqrt{6-4 \sqrt{2}}}$.
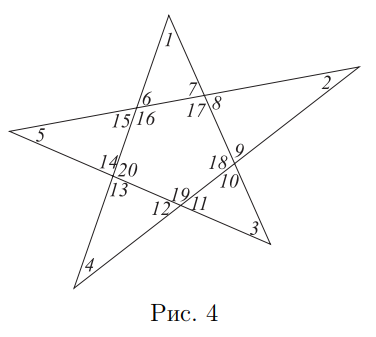
  9. Какова сумма углов, отмеченных на рисунке?

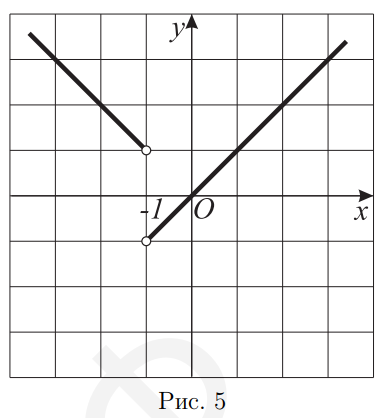
  10. Постройте график функции $y=\frac{|x+1|}{x+1} x$ (ответ изобразите на координатной системе ниже).

  11. Решите уравнение: $\frac{x^{2}}{x+2}+1=\frac{4}{x+2}$.
  12. На майскую прогулку вышла колонна туристов длиной 1200 м во главе с Мироном, они движутся с постоянной скоростью 6 км/ч. Из конца колонны в ее начало с указаниями бежит старший инструктор Александр со скоростью 9 км/ч. Передав указания Мирону, Александр с той же скоростью возвращается назад в конец колонны. Какое расстояние пробежит Александр?
    1. Докажите, что прямая, проходящая через середину меньшего основания трапеции и точку пересечения продолжений ее боковых сторон, проходит через середину большего основания.
    2. Найдите длину отрезка, соединяющего середины оснований трапеции, если прямые, содержащие ее боковые стороны, перпендикулярны, а длины оснований равны 2 и $5 .$
  14. Найдите сумму квадратов корней уравнения $x^{2}+(3+a) x+5 a-1=0$ и установите, при каких значениях $a$ она будет наименьшей.
Материалы школы Юайти
youit.school ©

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)


2015 год


Вариант 1



Часть В
К заданиям части В приведите только ответ, записав его в отведенном месте. Переписывать решение задачи в чистовик не нужно.

  1. Omвem: $x=\frac{5}{9}$.
  2. Omвem: 4.
  3. Оmвет: $x \in(-\infty ; 2) \cup(5 ;+\infty)$.
  4. Omвет: 31.
  5. Omвem: 3.
  6. Omвет: 0.
  7. Oтвет: 2.
  8. Oтвeт: $180^{\circ}$.
  9. -

    Часть C
  10. Oтвет: 1.
  11. Oтвет: 4,32 км.
  12. Omвет: 1,5.
  13. Omвет: $x_{1}^{2}+x_{2}^{2}=(a-2)^{2}+7$, наименьшее значение достигается при $a=1 .$
Материалы школы Юайти
youit.school ©

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)


2015 год


Вариант 1



Часть В
К заданиям части В приведите только ответ, записав его в отведенном месте. Переписывать решение задачи в чистовик не нужно.

  1. Упростите выражение: $a^{2} \sqrt{\frac{1}{a^{2}}-\frac{2 a-1}{a^{4}}}$, если $0<a<1 .$
    Решение. Упростим выражение: $ a^{2} \sqrt{\frac{1}{a^{2}}-\frac{2 a-1}{a^{4}}}=a^{2} \sqrt{\frac{(a-1)^{2}}{a^{4}}}=\frac{a^{2} \cdot|a-1|}{a^{2}}=|a-1|=1-a . $ При $0<a<1$ подмодульное выражение отрицательно, поэтому модуль раскроется со знаком минус. Omвет: $1-a$.
  2. Решите уравнение: $\left|x^{2}+3 x+3\right|=\left|x^{2}-6 x+8\right|$. Решение. Возможны два случая:
    (1) $x^{2}+3 x+3=x^{2}-6 x+8$
    $x^{2}+3 x+3=x^{2}-5 x=\frac{5}{9} ;$
    (2) $x^{2}+3 x+3=-\left(x^{2}-6 x+8\right) \quad 2 x^{2}-3 x+11=0 \quad D<0$, корней нет.
    Omвem: $x=\frac{5}{9}$.
  3. В остроугольном треугольнике $A B C$ известно, что $\angle A=45^{\circ}$, $B C-4 \sqrt{2} .$ Найдите радиус окружности, описанной около этого треугольника.

    Решение. Так как треугольник $A B C$ остроугольный, центр $O$ описанной около него окружности лежит внутри треугольника. Рассмотрим описанную около треугольника окружность. Угол $\angle B A C$ вписанный и опирается на дугу $B C$, а угол $\angle B O C$ центральный и опирается на ту же дугу. Значит, $\angle B O C=2 \angle B A C=90^{\circ}$ (рис. 1). Тогда треугольник $B O C$ равнобедренный и прямоугольный. По теореме Пифагора получаем $2 B O^{2}=B C^{2}=32$, откуда $B O=4 .$
    Omвem: 4.
  4. Решите неравенство: $(x-2)\left(x^{2}-2 x-3\right)>(x-2)^{2}(x-1)$.
    Решение. Перенесем правую часть неравенства и упростим выражение: $ (x-2)\left(x^{2}-2 x-3-(x-2)(x-1)\right)=(x-2)(x-5)>0 $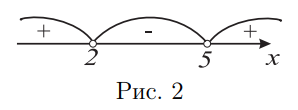
    Отметив на числовой прямой точки $x=2$ и $x=5$ и определив знак выражения $(x-2)(x-5)$ на каждом из трех промежутков (рис. 2), получим
    Оmвет: $x \in(-\infty ; 2) \cup(5 ;+\infty)$.
  5. На день рождения Карлсону подарили мешок с конфетами: шоколадными и карамельками. Всего конфет в мешке было меньше 100, причем соотношение шоколадных и карамелек было $9: 7 .$ Карлсон сразу же съел $20 \%$ всех конфет, причем $25 \%$ из них составляли карамельки. Сколько карамелек осталось в мешке?
    Решение. Поскольку в мешке соотношение шоколадных конфет и карамелек $9: 7$, общее количество конфет должно делиться на 16. При этом Карлсон сразу же съел 20% = $\frac{1}{5}$ всех конфет, следовательно, общее число конфет должно делиться на 5. Единственное подходящее число, меньшее 100, делящееся на 16 и 5, 一 это 80 .
    Если в мешке было всего 80 конфет, то среди них $\frac{9}{16} \cdot 80=45$ шоколадных и $\frac{7}{16} \cdot 80=35$ карамелек. Карлсон сразу съел $\frac{1}{5} \cdot 80=16$ конфет, из них $\frac{1}{4} \cdot 16=4$ карамельки. Значит в мешке осталась $35-4=31$ карамелька.
    Omвет: 31.
  6. Площадь треугольника $A B C$ равна $12 .$ Точка $M$ - середина $A C$ (рис. 3), точки $K$ и $L$ делят сторону $B C$ на три равные части. Найдите площадь заштрихованной части.

    Решение. Пусть $P$ - точка пересечения отрезков $B M$ и $A K$. Так как $B M-$ медиана в $\triangle A B C$, то $S_{C B M}=\frac{S_{A B C}}{2}=6$. По условию $B L: L C=2: 1 .$
    Кроме того, в треугольниках $B L M$ и $M L C$ общая высота. Тогда $S_{B L M}=\frac{2 S_{C B M}}{3}=4$. Треугольники $B P K$ и $B L M$ подобны, и коэффициент подобия равен $\frac{B K}{B L}=\frac{1}{2} .$ Значит, $S_{B P K}=\frac{S_{B L M}}{4}=1 .$ Откуда $S_{P K L M}=3 .$
    Omвem: 3.
  7. Какова последняя цифра числа $13^{2015}+13 ?$
    Решение. Отметим, что последняя цифра числа $13^{n}$ совпадает с последней цифрой числа $3^{n}$, и найдем последнюю цифру числа $3^{2015}+3 .$
    $3^{0}=\mathbf{1} \quad 3^{4}=8 \mathbf{1} \quad 3^{4 n}$ оканчивается на $\mathbf{1} ;$
    $3^{1}=3 \quad 3^{5}=243 \quad 3^{4 n+1}$ оканчивается на $\mathbf{3} ;$
    $\begin{array}{lcl}3^{2}=\mathbf{9} & 3^{6}=72 \mathbf{9} & 3^{4 n+2} \text { оканчивается на } \mathbf{9} ; \\ 3^{3}=2 \mathbf{7} & 3^{7}=2187 & 3^{4 n+3} \text { оканчивается на } \mathbf{7} .\end{array}$
    Поскольку $2015=4 \cdot 503+3$, последняя цифра числа $3^{2015}$ равна $7 .$ Значит, $3^{2015}+3$ оканчивается
    $\begin{aligned}&\text { Решение. Отметим, что последняя цифра числа } 13^{n} \text { совпадает с последней цифрой числа } 3^{n}, \text { и } \\&\text { найдем последнюю цифру числа } 3^{2015}+3 . \\&3^{0}=1 \quad 3^{4}=8 \mathbf{1} & 3^{4 n} \text { оканчивается на } \mathbf{1} ; \\&3^{1}=\mathbf{3} & 3^{5}=24 \mathbf{3} & 3^{4 n+1} \text { оканчивается на } \mathbf{3} ; \\&3^{2}=\mathbf{9} & 3^{6}=72 \mathbf{9} & 3^{4 n+2} \text { оканчивается на } \mathbf{9} ; \\&3^{3}=2 \mathbf{7} & 3^{7}=218 \mathbf{7} & 3^{4 n+3} \text { оканчивается на } \mathbf{7} . \\&\text { Поскольку } 2015=4 \cdot 503+3, \text { последняя цифра числа } 3^{2015} \text { равна } 7 . \text { Значит, } 3^{2015}+3 \text { оканчивается } \\&\text { на } 0 . & \\&\text { Оmвет: } 0 . & \\&\text { В8. Упростите выражение: } \frac{4}{\sqrt{2}+\sqrt{6-4 \sqrt{2}}} .\end{aligned}$ на 0.
    Omвет: 0.
  8. Упростите выражение: $\frac{4}{\sqrt{2}+\sqrt{6-4 \sqrt{2}}}$.
    Решение. Выделим полный квадрат под корнем: $6-4 \sqrt{2}=$ $=4-2 \cdot 2 \cdot \sqrt{2}+2=(2-\sqrt{2})^{2}$. Тогда: $\frac{4}{\sqrt{2}+\sqrt{6-4 \sqrt{2}}}=\frac{4}{\sqrt{2}+|2-\sqrt{2}|}=\frac{4}{\sqrt{2}+2-\sqrt{2}}=\frac{4}{2}=2$.
    Oтвет: 2.
  9. Какова сумма углов, отмеченных на рисунке?

    Решение. Вертикальные углы, отмеченные на рисунке числами 6 и 15,7 и 8,9 и 10,11 и 12,13 и 14 соответственно, образуют пары равных углов, поэтому искомая сумма углов равна $ \angle 1+\angle 2+\angle 3+\angle 4+\angle 5=5 \cdot 180^{\circ}-2 \angle 6-2 \angle 7-2 \angle 9-2 \angle 11-2 \angle 13=900^{\circ}-2(\angle 6+\angle 7+\angle 9+\angle 11+\angle 13) $ Углы, отмеченные числами $6,7,9,11,13$, смежные с углами пятиугольника, отмеченными числами $16,17,18,19$ и 20, сумма которых составляет $180^{\circ} \cdot 3=480^{\circ} .$ Значит, искомая сумма равна $ 900^{\circ}-2\left(5 \cdot 180^{\circ}-540^{\circ}\right)=180^{\circ} . $ Oтвeт: $180^{\circ}$.
  10. Постройте график функции $y=\frac{|x+1|}{x+1} x$ (ответ изобразите на координатной системе ниже).

    Решение. Данная функция определена при всех $x \neq-1 .$ Если $x>-1$, то строим часть прямой $y=x$. Если $x<-1$, то строим часть прямой $y=-x .$ График функции изображен на рис. $5 .$

    Часть C
    К заданиям части С нужно привести в чистовике полное решение и ответ.
  11. Решите уравнение: $\frac{x^{2}}{x+2}+1=\frac{4}{x+2}$.
    Решение. Перенесем правую часть уравнения налево и упростим выражение: $ \frac{x^{2}}{x+2}+1-\frac{4}{x+2}=\frac{x^{2}+(x+2)-4}{x+2}=\frac{x^{2}+x-2}{x+2}=\frac{(x+2)(x-1)}{x+2}=0 . $ Поскольку $(x+2)$ не может равняться 0 , единственный корень уравнения $x=1$.
    Oтвет: 1.
  12. На майскую прогулку вышла колонна туристов длиной 1200 м во главе с Мироном, они движутся с постоянной скоростью 6 км/ч. Из конца колонны в ее начало с указаниями бежит старший инструктор Александр со скоростью 9 км/ч. Передав указания Мирону, Александр с той же скоростью возвращается назад в конец колонны. Какое расстояние пробежит Александр?
    Решение. Разобьем задачу на две части: (1) Александр догоняет Мирона, (2) он возвращается назад в конец колонны.
    (1) Поскольку сперва Александр бежит по ходу движения колонны, скорость, с которой он догоняет Мирона, равна $9-6=3$ км/ч. Таким образом на то, чтобы догнать Мирона, Александр потратит $\frac{1,2}{3}=0,4$ часа.
    (2) При движении обратно Александр нагоняет конец колонны со скоростью $9+6=15$ км/ч. Следовательно на то, чтобы вернуться обратно, у него уйдет $\frac{1,2}{15}=0,08$ часа.
    Поскольку скорость Александра постоянна, пробежит он всего $9 \cdot(0,4+0,08)=9 \cdot 0,48=4,32$ км. Oтвет: 4,32 км.
    1. Докажите, что прямая, проходящая через середину меньшего основания трапеции и точку пересечения продолжений ее боковых сторон, проходит через середину большего основания.
    2. Найдите длину отрезка, соединяющего середины оснований трапеции, если прямые, содержащие ее боковые стороны, перпендикулярны, а длины оснований равны 2 и $5 .$
    Решение.
    1. Пусть $A B C D-$ трапеция с основаниями $A B$ и $C D(A B<C D) .$ Обозначим через $E$ точку пересечения прямых, содержащих ее боковые стороны, а через $P$ середину основания $A B$. Пусть $Q$ - точка пересечения прямых $E P$ и $C D$. В треугольниках $A E P$ и $D E Q$ : $\angle A E P-$ общий, $\angle E A P=\angle E D Q$ как соответственные для параллельных прямых $A P$ и $D Q$ и секущей $E D .$ Значит, $\triangle A E P \backsim \triangle E D Q .$ Получаем, что $\frac{A P}{D Q}=\frac{E P}{E Q} .$ Аналогично из подобия треугольников $E P B$ и $E C Q$ следует равенство $\frac{E P}{E Q}=\frac{P B}{C Q}$. Тогда $\frac{A P}{D Q}=\frac{P B}{Q C}$. Точка $P-$ середина $A B$, стало быть, $A P=P B$, но тогда $D Q=Q C$, что и требовалось доказать.
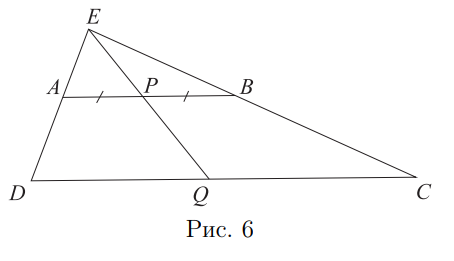
    2. По условию $\angle A E B=90^{\circ} .$ В силу доказанного выше утверждения, $E P$ и $E Q-$ медианы в прямоугольных треугольниках $A E B$ и $D E C$, поэтому $E P=\frac{A B}{2}=1, E Q=\frac{C D}{2}=2,5 .$ Тогда $P Q=$ $=E Q-E P=1,5$.
      Omвет: 1,5.
  14. Найдите сумму квадратов корней уравнения $x^{2}+(3+a) x+5 a-1=0$ и установите, при каких значениях $a$ она будет наименьшей.
    Решение. Посчитаем дискриминант и найдем значения параметра $a$, при которых уравнение имеет решение: $D=(3+a)^{2}-4(5 a-1)=a^{2}-14 a+13 \geqslant 0 \Leftrightarrow(a-13)(a-1) \geqslant 0 \Leftrightarrow a \geqslant 13$ или $a \leqslant 1 .$
    Пусть $x_{1}$ и $x_{2}-$ корни уравнения $x^{2}+(3+a) x+5 a-1=0$. Воспользуемся теоремой Виета: $ \left\{\begin{array}{l} x_{1}+x_{2}=-(3+a) \\ x_{1} \cdot x_{2}=5 a-1 \end{array}\right. $ Выразим сумму квадратов корней и воспользуемся найденными соотношениями: $ x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} \cdot x_{2}=(3+a)^{2}-2(5 a-1)=a^{2}-4 a+11=\left(a^{2}-4 a+4\right)+7=(a-2)^{2}+7 . $ Заметим, что при любом значении $a$ выражение $(a-2)^{2} \geqslant 0$, следовательно $x_{1}^{2}+x_{2}^{2}=(a-2)^{2}+7 \geqslant 7$. Равенство достигается при $a=2$, однако в таком случае $D<0$ и уравнение решений не имеет.
    При допустимых $a \in(-\infty ; 1] \cup[13 ;+\infty)$ наименьшее значение выражения $(a-2)^{2}+7$ равно 8 и достигается при $a=1$.
    Omвет: $x_{1}^{2}+x_{2}^{2}=(a-2)^{2}+7$, наименьшее значение достигается при $a=1 .$
Материалы школы Юайти