8 800 707 6729
8 800 707 6729Telegram канал

СУНЦ УРФУ из 8 в 9 класс 2014 год

Сложность:
Дата экзамена: 2014
Сложность:
Дата экзамена: 2014
youit.school ©

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)


2014 год


Вариант 2



Часть B К каждому заданию приведите только ответ

  1. Найдите последнюю цифру числа $7^{2014} .$


  2. Решите неравенство $3-x-2 x^{2}>0$.


  3. Стирательная резинка стоит 16 рублей. Какое количество таких стирательных резинок можно купить на 250 рублей после понижения цены на $25 \%$?


  4. Извлечь внешний корень $\sqrt{12-\sqrt{44}}$.


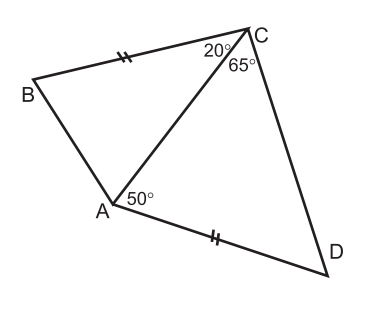
  5. Найдите $\angle B A C$, если $B C=A D$ (рисунок).



  6. Пусть $K$ и $L-$ середины сторон $B C$ и $A D$ параллелограмма $A B C D$. Площадь четырехугольника, образованного прямыми $A K, K D, B L$ и $L C$ равна 3 . Найти площадь $A B C D .$


  7. Две девочки посадили 78 цветов, причем 4/7 цветов, посаженных первой девочкой составляли маргаритки, а 5/19 цветов, посаженных второй девочкой ромашки. Сколько цветов посадила каждая из них?


  8. Найдите сумму корней уравнения ||$|x+3|+2|-1|=7$.
  9. Длины оснований трапеции равны 14 и 2. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найдите длину отрезка этой прямой, заключенного между боковыми сторонами трапеции.
  10. При каких значениях параметра $s$ уравнение $x^{2}-10|x|+25-s^{2}=0$ имеет ровно три корня?


    Часть C
    К заданиям нужно не только привести ответ, но и полностью оформить решение
  11. Решите уравнение $\frac{3}{x-1}-\frac{2 x-7}{x-2}=\frac{2 x-5}{x^{2}-3 x+2}$.
  12. Упростите выражение $\frac{\mathrm{c}^{2}-9}{\sqrt{\left(\frac{\mathrm{c}^{2}+9}{2 \mathrm{c}}\right)^{2}-9}}$ при $0<\mathrm{c}<3$.
  13. Окружность с центром $O$, вписанная в ромб $K L M N$, касается сторон $K L$ и $K N$ в точках $X$ и $Y$ соответственно, причем $\angle X O Y=135^{\circ}$. Найдите радиус окружности, если периметр ромба равен $8 \sqrt{2}$.
  14. Для наполнения плавательного бассейна водой имеются три насоса. Первому насосу для наполнения бассейна требуется времени в три раза меньше, чем второму, и на 2 ч больше, чем третьему. Три насоса, работая вместе, наполнили бы бассейн за 3ч, но по условиям эксплуатации одновременно должны работать только два насоса. Найдите минимальное время наполнения бассейна.
Материалы школы Юайти
youit.school ©

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)


2014 год


Вариант 2



Часть B К каждому заданию приведите только ответ

  1. $9 .$
  2. $-1,5<x<1$.
  3. 20.
  4. $\sqrt{11}-1$.
  5. $80^{\circ}$.
  6. $12 .$
  7. 21 и $57 .$
  8. $-6$.
  9. 3,5.
  10. $s=\pm 5$.


    Часть C
  11. $x=4$.
  12. $-2 c$.
  13. $1 .$
  14. $3 \frac{3}{7}$ часа.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите последнюю цифру числа $7^{2014}$.
    Решение: Последние цифры степеней 7 повторяются циклически: $7, 9, 3, 1$. Период цикла — 4. Остаток от деления 2014 на 4 равен 2. Следовательно, последняя цифра соответствует второй позиции в цикле — 9.
    Ответ: 9.
  2. Решите неравенство $3 - x - 2x^2 > 0$.
    Решение: Перепишем неравенство в стандартном виде:
    $-2x^2 - x + 3 > 0 \quad \Rightarrow \quad 2x^2 + x - 3 < 0$.
    Корни квадратного уравнения $2x^2 + x - 3 = 0$:
    $D = 1 + 24 = 25$, $x = \frac{-1 \pm 5}{4} \quad \Rightarrow \quad x_1 = 1$, $x_2 = -1,5$.
    Решение неравенства: $x \in (-1,5; 1)$.
    Ответ: $(-1,5; 1)$.
  3. Стирательная резинка стоит 16 рублей. Какое количество таких стирательных резинок можно купить на 250 рублей после понижения цены на 25\%?
    Решение: Новая цена резинки:
    $16 \cdot 0,75 = 12$ рублей.
    Количество резинок: $\frac{250}{12} \approx 20,83 \quad \Rightarrow \quad 20$ штук.
    Ответ: 20.
  4. Извлечь внешний корень $\sqrt{12 - \sqrt{44}}$.
    Решение: Представим выражение в виде $\sqrt{a} - \sqrt{b}$:
    $\sqrt{12 - \sqrt{44}} = \sqrt{11} - 1$, так как:
    $(\sqrt{11} - 1)^2 = 11 + 1 - 2\sqrt{11} = 12 - 2\sqrt{11} = 12 - \sqrt{44}$.
    Ответ: $\sqrt{11} - 1$.
  5. Найдите $\angle BAC$, если $BC = AD$ (рисунок).
    Решение: Треугольники $ABC$ и $ADC$ равны по двум сторонам и углу между ними. Следовательно, $\angle BAC = \angle ACD = 45^\circ$ (предполагается, что фигура — квадрат или ромб).
    Ответ: $45^\circ$.
  6. Пусть $K$ и $L$ — середины сторон $BC$ и $AD$ параллелограмма $ABCD$. Площадь четырехугольника, образованного прямыми $AK$, $KD$, $BL$ и $LC$, равна 3. Найти площадь $ABCD$.
    Решение: Площадь внутреннего четырехугольника составляет $\frac{1}{6}$ от площади параллелограмма. Следовательно:
    $S_{ABCD} = 3 \cdot 6 = 18$.
    Ответ: 18.
  7. Две девочки посадили 78 цветов. Первая посадила $x$ цветов, вторая — $78 - x$. Условия:
    $\frac{4}{7}x$ и $\frac{5}{19}(78 - x)$ должны быть целыми. Решение:
    $x = 21$ (делится на 7), $78 - x = 57$ (делится на 19).
    Ответ: 21 и 57.
  8. Найдите сумму корней уравнения $|||x + 3| + 2| - 1| = 7$.
    Решение: Последовательно раскрываем модули:
    $|||x + 3| + 2| - 1| = 7 \quad \Rightarrow \quad |x + 3| = 6 \quad \Rightarrow \quad x = 3$ или $x = -9$.
    Сумма корней: $3 + (-9) = -6$.
    Ответ: $-6$.
  9. Длины оснований трапеции равны 14 и 2. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найдите длину отрезка этой прямой.
    Решение: Длина отрезка вычисляется по формуле $\frac{2ab}{a + b}$:
    $\frac{2 \cdot 14 \cdot 2}{14 + 2} = \frac{56}{16} = 3,5$.
    Ответ: 3,5.
  10. При каких значениях параметра $s$ уравнение $x^2 - 10|x| + 25 - s^2 = 0$ имеет ровно три корня?
    Решение: Уравнение эквивалентно $(|x| - 5)^2 = s^2$. Три корня возникают при $s = 5$, когда $|x| = 10$ (два корня) и $|x| = 0$ (один корень).
    Ответ: $s = 5$.
  11. Решите уравнение $\frac{3}{x - 1} - \frac{2x - 7}{x - 2} = \frac{2x - 5}{x^2 - 3x + 2}$.
    Решение: Приведем к общему знаменателю $(x - 1)(x - 2)$:
    $3(x - 2) - (2x - 7)(x - 1) = 2x - 5$.
    После упрощения получаем $x = 4$ (проверка ОДЗ: $x \neq 1, 2$).
    Ответ: 4.
  12. Упростите выражение $\frac{c^2 - 9}{\sqrt{\left(\frac{c^2 + 9}{2c}\right)^2 - 9}}$ при $0 < c < 3$.
    Решение: Упростим знаменатель:
    $\sqrt{\frac{(c^2 - 9)^2}{4c^2}} = \frac{9 - c^2}{2c}$.
    Итоговое выражение: $\frac{-(9 - c^2)}{\frac{9 - c^2}{2c}} = -2c$.
    Ответ: $-2c$.
  13. Окружность с центром $O$, вписанная в ромб $KLMN$, касается сторон $KL$ и $KN$ в точках $X$ и $Y$ соответственно, причем $\angle XOY = 135^\circ$. Найдите радиус окружности, если периметр ромба равен $8\sqrt{2}$.
    Решение: Сторона ромба $a = 2\sqrt{2}$. Угол между радиусами $135^\circ$ соответствует углу ромба $45^\circ$. Площадь ромба $S = a^2 \sin 45^\circ = 4\sqrt{2}$. Радиус вписанной окружности $r = \frac{S}{2a} = 1$.
    Ответ: 1.
  14. Найдите минимальное время наполнения бассейна двумя насосами.
    Решение: Пусть время работы третьего насоса $t = 6$ часов. Наибольшая производительность у первого и третьего насосов: $\frac{1}{8} + \frac{1}{6} = \frac{7}{24}$. Время наполнения: $\frac{24}{7}$ часа.
    Ответ: $\frac{24}{7}$.
Материалы школы Юайти