Школа №1317 из 8 в 9 класс 2017 год вариант 1
Печать
youit.school ©
ГБОУ ШКОЛА №1317
2017 год
Демонстрационный вариант
Время на выполнение: 60 минут
- Вычислите: $$ \left(\left(2 \frac{3}{5}\right)^{-1}+\left(3 \frac{2}{3}\right)^{-2}\right) \cdot\left((-1,8)^{0}+(-1)^{-1}\right) $$
- Найдите значение выражения: $$ \frac{\sqrt{72}-4 \sqrt{2}+\sqrt{18}}{\sqrt{50}} $$
- Решите уравнение по формуле корней квадратного уравнения с чётным вторым коэффициентом: $9 x^{2}-132 x+123=0$.
- Медиана равнобедренного треугольника, проведённая к его основанию, равна 8 см. Основание равно 30 см. Найдите боковую сторону треугольника.
- Из 35 хозяйств деревни в 27 хозяйствах занимаются животноводством и в 33 - растениеводством. Сколько хозяйств в деревне занимаются и тем, и другим видом сельскохозяйственной деятельности?
- Постройте график функции:
- $f(x)=\sqrt{(x-3)^{2}}+2 ;$
- $h(x)=(\sqrt{x-3})^{2}+2$.
- B прямоугольнике ABCD (cм. pисyпок) $\angle \mathrm{CBK}=45^{\circ}, \mathrm{CD}=6 \mathrm{~cm}$. Найдите периметр прямоугольника, если $A K: K D=2: 3 .$
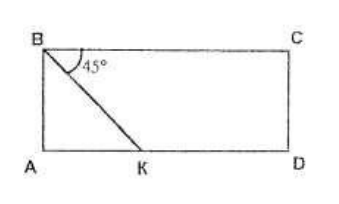
- Упростите выражение $\sqrt{4 a^{2}-4 a b+b^{2}}-\sqrt{4 b^{2}}$ при $a>0, b<0 .$
- Свежие грибы содержат 90 % влаги. Сушёные грибы содержат 20 % влаги. Сколько килограммов сушёных грибов получится из 64 кг свежих?
- Дан ромб $A B C D$. Диагональ $B D$ равна 10 см. Высота $D M$ равна 8 см. Найдите сторону ромба.
- От пристани А к пристани В, расстояние между которыми равно 180 км, отправился с постоянной скоростью первый теплоход. Через 2 ч после этого от пристани А по тому же маршруту отправился второй теплоход, скорость которого была на 3 км/ч больше, чем скорость первого. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.
- При каком значении $q$ уравнение $4 x^{2}+8 x+q=0$ имеет корни, один из которых на 3 больше другого?
Материалы школы Юайти
youit.school ©
Ответы:
- 0
- 1
- 41/3;1
- 17
- 25
- -
- 36
- 2a+b
- 8
- 8+1/3;25/3
- 15
- -5
Материалы школы Юайти
youit.school ©
Решения задач
- Вычислите:
$
\left(\left(2 \frac{3}{5}\right)^{-1}+\left(3 \frac{2}{3}\right)^{-2}\right) \cdot\left((-1,8)^{0}+(-1)^{-1}\right)$
Решение:
Преобразуем дроби:
$2\frac{3}{5} = \frac{13}{5} \Rightarrow \left(2\frac{3}{5}\right)^{-1} = \frac{5}{13}$
$3\frac{2}{3} = \frac{11}{3} \Rightarrow \left(3\frac{2}{3}\right)^{-2} = \left(\frac{3}{11}\right)^2 = \frac{9}{121}$
Вычислим степени:
$(-1,8)^0 = 1$, $(-1)^{-1} = -1$
Сумма в первых скобках: $\frac{5}{13} + \frac{9}{121} = \frac{605 + 117}{1573} = \frac{722}{1573}$
Сумма во вторых скобках: $1 + (-1) = 0$
Итоговое значение: $\frac{722}{1573} \cdot 0 = 0$
Ответ: 0.
- Найдите значение выражения:
$
\frac{\sqrt{72}-4 \sqrt{2}+\sqrt{18}}{\sqrt{50}}$
Решение:
Упростим корни:
$\sqrt{72} = 6\sqrt{2}$, $\sqrt{18} = 3\sqrt{2}$, $\sqrt{50} = 5\sqrt{2}$
Подставим в выражение:
$\frac{6\sqrt{2} - 4\sqrt{2} + 3\sqrt{2}}{5\sqrt{2}} = \frac{5\sqrt{2}}{5\sqrt{2}} = 1$
Ответ: 1.
- Решите уравнение по формуле корней квадратного уравнения с чётным вторым коэффициентом: $9 x^{2}-132 x+123=0$
Решение:
Формула для чётного коэффициента $b = 2k$:
$x = \frac{-k \pm \sqrt{k^2 - ac}}{a}$
Здесь $a = 9$, $b = -132 \Rightarrow k = -66$, $c = 123$
Дискриминант:
$D_1 = (-66)^2 - 9 \cdot 123 = 4356 - 1107 = 3249 = 57^2$
Корни:
$x = \frac{66 \pm 57}{9}$
$x_1 = \frac{66 + 57}{9} = \frac{123}{9} = 13\frac{2}{3}$, $x_2 = \frac{66 - 57}{9} = 1$
Ответ: $1$ и $13\frac{2}{3}$.
- Медиана равнобедренного треугольника, проведённая к его основанию, равна 8 см. Основание равно 30 см. Найдите боковую сторону треугольника.
Решение:
В равнобедренном треугольнике медиана к основанию является высотой. По теореме Пифагора:
Боковая сторона $= \sqrt{15^2 + 8^2} = \sqrt{225 + 64} = \sqrt{289} = 17$ см
Ответ: 17 см.
- Из 35 хозяйств деревни в 27 хозяйствах занимаются животноводством 33 - растениеводством. Сколько хозяйств в деревне занимаются и тем, и другим видом сельскохозяйственной деятельности?
Решение:
По формуле включений-исключений:
$27 + 33 - 35 = 25$ хозяйств
Ответ: 25.
- Постройте график функции:
- $f(x)=\sqrt{(x-3)^{2}}+2$
Решение:
$\sqrt{(x-3)^2} = |x-3|$, значит $f(x) = |x-3| + 2$ — график "уголок" с вершиной в точке (3,2)
Ответ: V-образный график с вершиной (3,2).
- $h(x)=(\sqrt{x-3})^{2}+2$
Решение:
$(\sqrt{x-3})^2 = x-3$ при $x \geq 3$, значит $h(x) = x - 3 + 2 = x - 1$ для $x \geq 3$
Ответ: Прямая $y = x - 1$ при $x \geq 3$.
- $f(x)=\sqrt{(x-3)^{2}}+2$
- -
- Упростите выражение $\sqrt{4 a^{2}-4 a b+b^{2}}-\sqrt{4 b^{2}}$ при $a>0, b<0$
Решение:
$\sqrt{4a^2 -4ab +b^2} = \sqrt{(2a - b)^2} = |2a - b| = 2a - b$ (т.к. $a>0$, $b<0$)
$\sqrt{4b^2} = 2|b| = -2b$ (т.к. $b<0$)
Итог: $2a - b - (-2b) = 2a + b$
Ответ: $2a + b$.
- Свежие грибы содержат 90% влаги. Сушёные грибы содержат 20% влаги. Сколько килограммов сушёных грибов получится из 64 кг свежих?
Решение:
Сухое вещество в свежих грибах: $64 \cdot 10% = 6.4$ кг
В сушёных грибах сухое вещество составляет 80\%:
$6.4 : 80% = 6.4 \cdot \frac{100}{80} = 8$ кг
Ответ: 8 кг.
- -
- От пристани А к пристани В, расстояние между которыми равно 180 км, отправился с постоянной скоростью первый теплоход. Через 2 ч после этого от пристани А по тому же маршруту отправился второй теплоход, скорость которого была на 3 км/ч больше, чем скорость первого. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.
Решение:
Пусть скорость первого $x$ км/ч, тогда второго $x+3$ км/ч
Время первого: $\frac{180}{x}$, второго: $\frac{180}{x+3}$
Разница времени: $\frac{180}{x} - \frac{180}{x+3} = 2$
Решаем уравнение:
$180(x+3) - 180x = 2x(x+3)$
$540 = 2x^2 + 6x \Rightarrow x^2 + 3x - 270 = 0$
Корни: $x = \frac{-3 \pm \sqrt{9 + 1080}}{2} = \frac{-3 \pm 33}{2}$
$x = 15$ км/ч
Ответ: 15 км/ч.
- При каком значении $q$ уравнение $4 x^{2}+8 x+q=0$ имеет корни, один из которых на 3 больше другого?
Решение:
Пусть корни $x_1$ и $x_2 = x_1 + 3$
По теореме Виета:
$x_1 + x_2 = -2$, $x_1 x_2 = \frac{q}{4}$
Подставляем $x_2 = x_1 + 3$:
$x_1 + x_1 + 3 = -2 \Rightarrow 2x_1 = -5 \Rightarrow x_1 = -2.5$, $x_2 = 0.5$
Произведение корней: $-2.5 \cdot 0.5 = -1.25 = \frac{q}{4} \Rightarrow q = -5$
Ответ: $q = -5$.
Материалы школы Юайти