Школа №67 из 7 в 8 класс 2019 год

ГИМНАЗИЯ №1567

2019 год

ЧАСТЬ 1

1. (2 балла) Вычислите $\left(-\frac{3}{4}\right)^{3}+\frac{3^{3}}{4}-\frac{3}{(-4)^{3}}$
2. (2 балла) Найдите корень уравнения $\frac{x+2}{4}-\frac{x}{2}=-1$
3. (2 балла) На рисунке найдите график функции $y=-\frac{1}{2} x+1$
   
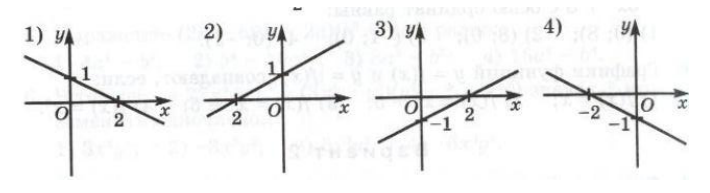
4. (2 балла) Укажите номера верных утверждений (номера указываются без запятых, например, 1234):
   1) Высота треугольника всегда лежит внутри треугольника.
   2) Медиана - это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
   3) В равнобедренном треугольнике медиана совпадает с биссектрисой, проведенной из той же вершины.
   4) В равностороннем треугольнике все углы равны.
5. (2 балла) Два велосипедиста отправились одновременно на встречу друг другу из двух пунктов, расстояние между которыми 60км, и встретились через 2 ч. Определите скорость каждого велосипедиста, если у одного она на 2 км/ч больше, чем у другого.
6. (2 балла) При каком значении переменной $n$ значение выражения $9(3 n-1)$ на 14 больше значения выражения $2(13 n+7)$.
7. (2 балла) Упростите выражение $(x-1)^{2}+(x-3)(3+x)-(x+2)(2 x-5)$ и укажите номер правильного ответа в бланке
   

   1	$-3 x-18$
   2	$x+6$
   3	$2-x$
   4	$-(x+2)$

8. (2 балла) Найдите стороны равнобедренного треугольника, периметр которого равен 96 см, а основание на 6 см больше боковой стороны.
   
   
   Часть2.
9. (6 баллов) Разложите на множители:
   • $-18 x^{3} y^{3}-9 x y$;
     
   • $9 x^{2}-(3 x-1)^{2}$;
     
   • $2 x-8 y-a x+4 a y$.
     
10. (4 баллов) Решите уравнение $\left(x^{2}+7 x\right)-4 x-28=0$.
11. (6 баллов) Задайте формулой линейную функцию, график которой параллелен графику функции $y=-x+2004$ и пересекается с графиком функции $y=5 x+1$ в точке, лежащей на оси ординат.
12. (6 баллов)При каком значении $m$ уравнение $(m+1) x=m$:
    • Имеет ровно один корень;
    • имеет бесконечное множество корней;
    • имеет хотя бы один корень;
    • не имеет корней;
    • имеет корень $x=0$;
    • имеет корень $x=-2$.

Решения задач

1. Вычислите $\left(-\frac{3}{4}\right)^{3}+\frac{3^{3}}{4}-\frac{3}{(-4)^{3}}$
   Решение:
   $\left(-\frac{3}{4}\right)^3 = -\frac{27}{64}$
   $\frac{3^3}{4} = \frac{27}{4}$
   $\frac{3}{(-4)^3} = \frac{3}{-64} = -\frac{3}{64}$
   Суммируем: $-\frac{27}{64} + \frac{27}{4} - \left(-\frac{3}{64}\right) = -\frac{27}{64} + \frac{432}{64} + \frac{3}{64} = \frac{408}{64} = 6,375$
   Ответ: 6,375.
   
   
2. Найдите корень уравнения $\frac{x+2}{4}-\frac{x}{2}=-1$
   Решение:
   Умножим обе части на 4:
   $(x + 2) - 2x = -4$
   $-x + 2 = -4$
   $-x = -6 \Rightarrow x = 6$
   Ответ: 6.
   
   
3. -
   
4. Укажите номера верных утверждений:
   1) Неверно (высота может лежать вне треугольника в тупоугольном треугольнике).
   2) Верно (определение медианы).
   3) Неверно (совпадает только в равностороннем треугольнике).
   4) Верно (свойство равностороннего треугольника).
   Ответ: 24.
   
   
5. Определите скорости велосипедистов:
   Решение: Пусть скорость первого $x$ км/ч, тогда второго $(x + 2)$ км/ч.
   Суммарная скорость: $x + x + 2 = 2x + 2$ км/ч.
   За 2 часа они проехали $2(2x + 2) = 60$ км.
   $4x + 4 = 60 \Rightarrow 4x = 56 \Rightarrow x = 14$ км/ч (первый), $14 + 2 = 16$ км/ч (второй).
   Ответ: 14 и 16.
   
   
6. Найдите $n$:
   Решение: Составим уравнение:
   $9(3n - 1) - 2(13n + 7) = 14$
   $27n - 9 - 26n - 14 = 14$
   $n - 23 = 14 \Rightarrow n = 37$
   Ответ: 37.
   
   
7. Упростите выражение:
   $(x-1)^2 + (x-3)(3+x) - (x+2)(2x-5)$
   Раскроем скобки:
   $x^2 - 2x + 1 + x^2 - 9 - (2x^2 - 5x + 4x - 10)$
   $2x^2 - 2x - 8 - 2x^2 + x + 10 = -x + 2$
   Ответ: 3.
   
   
8. Найдите стороны треугольника:
   Решение: Пусть боковая сторона $x$ см, тогда основание $(x + 6)$ см.
   Периметр: $2x + x + 6 = 96 \Rightarrow 3x = 90 \Rightarrow x = 30$ см (боковые), основание $36$ см.
   Ответ: 30 см, 30 см, 36 см.
   
   
9. Разложите на множители:
   
   • $-18x^3y^3 - 9xy = -9xy(2x^2y^2 + 1)$
   • $9x^2 - (3x - 1)^2 = (3x)^2 - (3x - 1)^2 = (6x - 1)(1)$
   • $2x - 8y - ax + 4ay = 2(x - 4y) - a(x - 4y) = (2 - a)(x - 4y)$
   
   
   
10. Решите уравнение:
    $(x^2 + 7x) - 4x - 28 = 0$
    Группируем:
    $x(x + 7) - 4(x + 7) = 0 \Rightarrow (x - 4)(x + 7) = 0$
    Корни: $x = 4$, $x = -7$
    Ответ: 4; -7.
    
    
11. Задайте линейную функцию:
    Условие параллельности: $k = -1$. Пересечение на оси ординат ($x = 0$):
    $y = 5\cdot0 + 1 = 1$. Значит, уравнение: $y = -x + 1$
    Ответ: $y = -x + 1$.
    
    
12. Исследуйте уравнение $(m + 1)x = m$:
    • Один корень: $m \neq -1$
    • Бесконечно корней: нет решений (при $m + 1 = 0$ и $m = 0$ противоречие)
    • Хотя бы один корень: $m \neq -1$
    • Нет корней: $m = -1$
    • Корень $x = 0$: невозможно (подстановка даёт $0 = m$)
    • Корень $x = -2$: $(m + 1)(-2) = m \Rightarrow -2m - 2 = m \Rightarrow -3m = 2 \Rightarrow m = -\frac{2}{3}$
    Ответы:
    • $m \neq -1$
    • Нет решений
    • $m \neq -1$
    • $m = -1$
    • Нет решений
    • $m = -\frac{2}{3}$