8 800 707 6729
8 800 707 6729Telegram канал

Лицей № 456 из 5 в 6 класс 2015 год

Школа:
Школа не выбрана
Сложность:
Дата экзамена: 2015
Школа:
Школа не выбрана
Сложность:
Дата экзамена: 2015
youit.school ©

ЛИЦЕЙ №1535


2015 год

Вариант 090114



Инструкция: 1. Вступительное испытание проводится в письменной форме. Использование калькуляторов, компьютеров и любых видов справочных пособий запрещено. На время проведения экзамена необходимо отключить мобильные телефоны и любые другие средства коммуникации. Взаимные консультации учащихся запрещены. Работа выполняется и оформляется исключительно на листах, выданных Вам экзаменаторами. Нарушение любого пункта инструкции влечѐт удаление учащегося из аудитории и выставление ему за вступительное испытание по математике отметки «0». 2. Ответом на задания части I может быть или целое число, или конечная десятичная дробь, или несократимая обыкновенная дробь (с выделенной целой частью). Полученный Вами ответ без указания единиц измерения следует вписать в соответствующую строку бланка ответов справа от номера задачи. Цифры, знак "минус", дробные черты, десятичные запятые должны быть написаны чѐтко, разборчиво. При проверке заданий части I проверяется только бланк с Вашими ответами. Претензии, связанные с неразборчиво написанными цифрами, при апелляции не принимаются. 3. Часть II предлагаемой Вам работы содержат два задания, к которым необходимо привести развѐрнутое решение. Для записи решений и ответов используйте специальные листы, выданные Вам экзаменаторами. Решения заданий можно излагать в произвольном порядке. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.


Часть 1

  1. (2 балла). Сократите дробь и найдите ее значение при $\mathrm{x}=998 .$ $$ \frac{5 x-10}{4-x^{2}} $$
  2. (3 балла) Решите уравнение, в ответе запишите сумму квадратов корней. $$ \left(13-x^{2}\right) \cdot\left(5 x^{2}+3 x\right)=0 $$
  3. (3 балла) Вычислите: $$ -0,06 \cdot\left(-1 \frac{5}{6}\right):(2,65: 2,5-1,1) $$
  4. (3 балла). Решите уравнение: $$ 7 x^{2}-3 x+8=2 x^{2}-13 x+6 $$
  5. (3 балла). Найти значение выражения: $$ (\sqrt{7}-\sqrt{2})^{2}(9+\sqrt{56}) $$
  6. (3 балла). Вычислите координаты точки А.

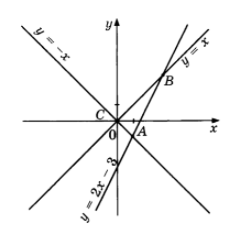
  7. (4 балла). При каком значении b один из корней уравнения $\mathrm{x}^{2}-7 \mathrm{x}+\mathrm{b}=0$ равен 13 ? Найдите другой корень уравнения. В ответе запишите значение выражения $3 \mathrm{x}_{1}+2 \mathrm{x}_{2}$, где $\mathrm{x}_{1}$ и $\mathrm{x}_{2}-$ корни квадратного уравнения.
  8. (5 баллов). Решите уравнение $$ \frac{x^{2}-12}{x^{2}-4}-\frac{x}{2-x}=1 $$
  9. (5 баллов). Имеется два сплава. Первый содержит 5% никеля, второй $40 \%$ никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий $25 \%$ никеля. На сколько килограммов масса первого сплава меньше массы второго?

    Часть 2
  10. (7 баллов).
    1. Упростить выражение $$ \left(\frac{42 a}{a^{2}-18 a+81}-\frac{5 a}{9-a}\right): \frac{5 a-3}{a^{2}-81}-\frac{9(a+9)}{a-9} $$
    2. Привести пример переменной а при которой не имеет смысл выражение.
  11. (6 баллов). Из пункта А в пункт В, удаленный на расстояние 100 км, отправился междугородний автобус. Из-за ненастной погоды он ехал со скоростью на 10 км/ч меньшей, чем предполагалось по расписанию и поэтому прибыл в пункт В с опозданием на 30 минут. С какой скоростью должен был ехать автобус по расписанию?
  12. (6 баллов).
    1. Построить в одной системе координат графики функций $\mathrm{y}=\frac{6}{\mathrm{x}}$ и $\mathrm{y}=\mathrm{x}+1 .$
    2. С помощью построенных графиков решите систему уравнений $$ \left\{\begin{array}{c} y=\frac{6}{x} \\ y=x+1 \end{array}\right. $$
    3. С помощью построенных графиков указать множество всех решений неравенства $\frac{6}{x}>x+1 .$
Материалы школы Юайти
youit.school ©
Ответы:
1) -000.5 2) 26.36 3) 2.75 4) (-5+-sqrt(15))/5 5) 25 6) (1; -1) 7) 27 или 8 8) -4 9) 25 10) a+9 при a=+-9 11) 50 12) a) - б) (-3; 2) и (2; 3) в) (-inf; -3) и (0; 2)
Материалы школы Юайти