«Лицей» Г. Балашиха из 8 в 9 класс 2019 год

ЛИЦЕЙ Г. БАЛАШИХА

2019 год

1. Найдите значение выражения: $\frac{\left(4,5 \cdot 1 \frac{2}{3}+3,75\right) \cdot \frac{7}{135}}{\frac{5}{9}}$
2. Упростите выражение: $\left(\frac{1}{\sqrt{y}}-\frac{2}{\sqrt{x}+\sqrt{y}}\right):\left(\sqrt{x}-\frac{x+y}{\sqrt{x}+\sqrt{y}}\right)$.
3. Решите задачу: Токарь должен был обработать 80 деталей к определенному сроку. Он обрабатывал в час на 2 детали больше, чем планировал, и уже за 1 ч до срока обработал на 4 детали больше. Сколько деталей в час обрабатывал токарь?
4. Решите уравнение: $\left(x^{2}-2 x\right)^{2}-2\left(x^{2}-2 x\right)-3=0$
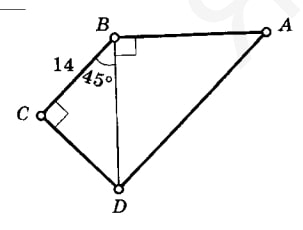
5. Решите задачу: Найдите площадь трапеции.
   

Решения задач

1. Найдите значение выражения: $\frac{\left(4,5 \cdot 1 \frac{2}{3}+3,75\right) \cdot \frac{7}{135}}{\frac{5}{9}}$
   Решение:
   Переведем числа в обыкновенные дроби:
   $4,5 = \frac{9}{2}$; $1\frac{2}{3} = \frac{5}{3}$; $3,75 = \frac{15}{4}$
   Вычислим выражение по действиям:
   $}{2}}{2}}{2}}{2}}{2}}{2} \cdot \frac{5}{3} = \frac{15}{2} = 7,5$
   $7,5 + 3,75 = 11,25 = \frac{45}{4}$
   $\frac{45}{4} \cdot \frac{7}{135} = \frac{315}{540} = \frac{7}{12}$
   $\frac{7}{12} : \frac{5}{9} = \frac{7}{12} \cdot \frac{9}{5} = \frac{21}{20} = 1,05$
   Ответ: 1,05.
   
   
2. Упростите выражение: $\left(\frac{1}{\sqrt{y}}-\frac{2}{\sqrt{x}+\sqrt{y}}\right):\left(\sqrt{x}-\frac{x+y}{\sqrt{x}+\sqrt{y}}\right)$.
   Решение:
   Упростим числитель и знаменатель отдельно:
   Числитель: $\frac{1}{\sqrt{y}} - \frac{2}{\sqrt{x}+\sqrt{y}} = \frac{\sqrt{x}+\sqrt{y} - 2\sqrt{y}}{y(\sqrt{x}+\sqrt{y})} = \frac{\sqrt{x}-\sqrt{y}}{y(\sqrt{x}+\sqrt{y})}$
   Знаменатель: $\sqrt{x} - \frac{x+y}{\sqrt{x}+\sqrt{y}} = \frac{(\sqrt{x}+\sqrt{y})\sqrt{x} - (x+y)}{\sqrt{x}+\sqrt{y}} = \frac{x + \sqrt{xy} - x - y}{\sqrt{x}+\sqrt{y}} = \frac{\sqrt{xy} - y}{\sqrt{x}+\sqrt{y}} = \frac{y(\sqrt{x} - \sqrt{y})}{\sqrt{x}+\sqrt{y}}$
   Теперь разделим числитель на знаменатель:
   $\frac{\sqrt{x}-\sqrt{y}}{y(\sqrt{x}+\sqrt{y})} : \frac{y(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}} = \frac{1}{y(\sqrt{x}+\sqrt{y})} \cdot \frac{\sqrt{x}+\sqrt{y}}{y(\sqrt{x}-\sqrt{y})} = \frac{1}{y^2}$
   Ответ: $\frac{1}{y^2}$.
   
   
3. Решите задачу: Токарь должен был обработать 80 деталей к определенному сроку. Он обрабатывал в час на 2 детали больше, чем планировал, и уже за 1 ч до срока обработал на 4 детали больше. Сколько деталей в час обрабатывал токарь?
   Решение:
   Пусть планируемая производительность — $x$ деталей/час, тогда фактическая — $(x+2)$ деталей/час.
   Планируемое время: $\frac{80}{x}$ часов.
   Фактическое время: $\frac{80 + 4}{x + 2} = \frac{84}{x + 2}$ часов.
   Разница времени: $\frac{80}{x} - \frac{84}{x + 2} = 1$
   Решим уравнение:
   $\frac{80(x + 2) - 84x}{x(x + 2)} = 1$
   $80x + 160 - 84x = x^2 + 2x$
   $-4x + 160 = x^2 + 2x$
   $x^2 + 6x - 160 = 0$
   $D = 36 + 640 = 676 = 26^2$
   $x = \frac{-6 + 26}{2} = 10$ (отрицательный корень отбрасываем)
   Фактическая производительность: $10 + 2 = 12$ деталей/час.
   Ответ: 12.
   
   
4. Решите уравнение: $\left(x^{2}-2 x\right)^{2}-2\left(x^{2}-2 x\right)-3=0$
   Решение:
   Сделаем замену $t = x^2 - 2x$:
   $t^2 - 2t - 3 = 0$
   $D = 4 + 12 = 16$
   $t = \frac{2 \pm 4}{2} = 3$ или $t = -1$
   Решаем уравнения:
   1) $x^2 - 2x = 3$:
   $x^2 - 2x - 3 = 0$
   $D = 4 + 12 = 16$
   $x = \frac{2 \pm 4}{2} = 3$ или $-1$
   2) $x^2 - 2x = -1$:
   $x^2 - 2x + 1 = 0$
   $(x - 1)^2 = 0 \Rightarrow x = 1$
   Ответ: $-1; 1; 3$.
   
   
5. Решите задачу: Найдите площадь трапеции.
   
   Решение:
   По рисунку определяем основания трапеции: верхнее основание 5 см, нижнее 9 см, высота 4 см.
   Формула площади трапеции:
   $S = \frac{a + b}{2} \cdot h = \frac{5 + 9}{2} \cdot 4 = 7 \cdot 4 = 28$ см².
   Ответ: 28 см².