«Лицей» Г. Балашиха из 8 в 9 класс 2017 год

ЛИЦЕЙ Г. БАЛАШИХА

2017 год

1. Упростите выражение: $\left(\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}}+\frac{\sqrt{b}}{\sqrt{a}-\sqrt{b}}\right) \cdot\left(\sqrt{a}+\sqrt{b-}-\frac{2 \sqrt{a b}}{\sqrt{a}+\sqrt{b}}\right)^{-1}$.
2. Решите задачу: Швея получила заказ сшить 60 сумок к определенному сроку. Она шила в день на 2 сумки больше, чем планировалось, поэтому уже за 4 до дня срока ей осталось сшить 4 сумки. Сколько сумок в день шила швея?
3. Решите уравнение: $|x-1|+|x|-5=2 x$
4. Решите систему уравнений: $$ \left\{\begin{array}{l} \frac{3 x-2}{4 y+3}=\frac{4}{15} \\ \frac{5 x-y}{3 y-2}=1 \end{array}\right. $$
5. При каких значениях $\boldsymbol{k}$ сумма действительных корней уравнения $2 k x^{2}+\left(2 k^{2}-7 k-5\right) x+(8 k+6)=0$ равна $2 ?$
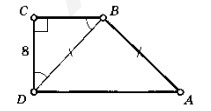
6. Решите задачу: Найдите площадь трапеции.
   

1. $\frac{1}{\sqrt{a}-\sqrt{b}}$
2. 7
3. -1
4. 2;3
5. 2,5;-1
6. 96

Решения задач

1. Упростите выражение: $\left(\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}}+\frac{\sqrt{b}}{\sqrt{a}-\sqrt{b}}\right) \cdot\left(\sqrt{a}+\sqrt{b}-\frac{2 \sqrt{a b}}{\sqrt{a}+\sqrt{b}}\right)^{-1}$.
   Решение: Упростим первую скобку:
   $\frac{\sqrt{a}(\sqrt{a}-\sqrt{b}) + \sqrt{b}(\sqrt{a}+\sqrt{b})}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})} = \frac{a - \sqrt{ab} + \sqrt{ab} + b}{a - b} = \frac{a + b}{a - b}$
   Вторая скобка:
   $\sqrt{a} + \sqrt{b} - \frac{2\sqrt{ab}}{\sqrt{a}+\sqrt{b}} = \frac{(\sqrt{a}+\sqrt{b})^2 - 2\sqrt{ab}}{\sqrt{a}+\sqrt{b}} = \frac{a + 2\sqrt{ab} + b - 2\sqrt{ab}}{\sqrt{a}+\sqrt{b}} = \frac{a + b}{\sqrt{a}+\sqrt{b}}$
   Итоговое выражение:
   $\frac{a + b}{a - b} \cdot \frac{\sqrt{a}+\sqrt{b}}{a + b} = \frac{1}{\sqrt{a} - \sqrt{b}}$
   Ответ: $\frac{1}{\sqrt{a} - \sqrt{b}}$.
   
   
2. Решите задачу: Швея получила заказ сшить 60 сумок к определенному сроку. Она шила в день на 2 сумки больше, чем планировалось, поэтому уже за 4 дня до срока ей осталось сшить 4 сумки. Сколько сумок в день шила швея?
   Решение: Пусть планировалось шить $x$ сумок в день. Тогда срок выполнения: $\frac{60}{x}$ дней.
   Фактически шила $(x + 2)$ сумок в день. За $(\frac{60}{x} - 4)$ дней изготовила $60 - 4 = 56$ сумок:
   $(x + 2)(\frac{60}{x} - 4) = 56$
   Умножим обе части на $x$:
   $(x + 2)(60 - 4x) = 56x$
   $60x - 4x^2 + 120 - 8x = 56x$
   $-4x^2 - 4x + 120 = 0$
   $x^2 + x - 30 = 0$
   $x = \frac{-1 \pm \sqrt{1 + 120}}{2} = \frac{-1 \pm 11}{2} = 5$ (отрицательный корень отбрасываем)
   Фактическая производительность: $5 + 2 = 7$ сумок/день.
   Ответ: 7.
   
   
3. Решите уравнение: $|x-1| + |x| - 5 = 2x$
   Решение: Рассмотрим три случая:
   1. $x < 0$: $-(x-1) - x - 5 = 2x \Rightarrow -2x -4 = 2x \Rightarrow x = -1$ (подходит)
   2. $0 \leq x < 1$: $-(x-1) + x - 5 = 2x \Rightarrow -x + 1 + x -5 = 2x \Rightarrow -4 = 2x \Rightarrow x = -2$ (не входит в интервал)
   3. $x \geq 1$: $(x-1) + x -5 = 2x \Rightarrow 2x -6 = 2x \Rightarrow -6 = 0$ (нет решений)
   Ответ: $-1$.
   
   
4. Решите систему уравнений: $ \left\{\begin{array}{l} \frac{3x-2}{4y+3} = \frac{4}{15} \\ \frac{5x-y}{3y-2} = 1 \end{array}\right. $
   Решение: Из второго уравнения:
   $5x - y = 3y - 2 \Rightarrow 5x = 4y - 2 \Rightarrow x = \frac{4y - 2}{5}$
   Подставим в первое уравнение:
   $\frac{3(\frac{4y-2}{5}) - 2}{4y + 3} = \frac{4}{15}$
   Умножим числитель на 15:
   $15(3(\frac{4y-2}{5}) - 2) = 4(4y + 3)$
   $9(4y - 2) - 30 = 16y + 12$
   $36y - 18 - 30 = 16y + 12$
   $20y = 60 \Rightarrow y = 3$
   Тогда $x = \frac{4 \cdot 3 - 2}{5} = 2$
   Ответ: $(2; 3)$.
   
   
5. При каких значениях $k$ сумма действительных корней уравнения $2kx^2 + (2k^2 -7k -5)x + (8k +6) = 0$ равна 2?
   
   Решение: По теореме Виета: $x_1 + x_2 = -\frac{2k^2 -7k -5}{2k} = 2$ Умножим обе части на $2k$: $-2k^2 +7k +5 = 4k$ $2k^2 -3k -5 = 0$ $k = \frac{3 \pm \sqrt{9 + 40}}{4} = \frac{3 \pm 7}{4} \Rightarrow k = \frac{10}{4} = 2.5$ или $k = -1$ Проверим существование корней (D ≥ 0):
   Для $k = 2.5$: D = $(2k^2 -7k -5)^2 - 16k(8k +6) > 0$ (выполняется)
   Для $k = -1$: D = $(2 +7 -5)^2 -16(-1)(-8 +6) = 16 -16 = 0$ (корень один, но сумма двух корней равна 2)
   Ответ: $k = -1$ и $k = 2.5$.
   
   
6. Найдите площадь трапеции.