Интеллектуал КЕМГУ из 5 в 6 класс 2019 год

ИНТЕЛЛЕКТУАЛ КЕМГУ

2019 год

Вариант 1

1. Сумма двух натуральных чисел равна 474. Одно из них оканчивается цифрой $1 .$ Если эту цифру зачеркнуть, то получиться второе число. Найдите эти числа.
2. В поход отправились учащиеся $5-\mathrm{x}$ и $6-\mathrm{x}$ классов. Мальчиков было 16 ; шестиклассниц и шестиклассников всего 24; пятиклассниц столько, сколько шестиклассников (мальчиков из 6 класса). Сколько всего детей отправилось в поход?
3. Что быстрее: проехать весь путь на велосипеде или половину пути проехать на мотоцикле, а вторую половину пройти пешком, если скорость мотоцикла в два раза больше скорости велосипеда, а скорость велосипеда в свою очередь, в два раза больше скорости пешехода?
4. Даны три прямые. На каждой прямой - две точки. Сколько всего точек? Укажите все варианты.
5. Разрежьте фигуры, изображенные на рисунке, на четыре равные (одинаковые) части.
   
   
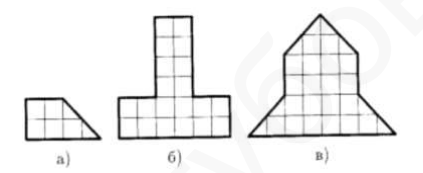
6. Матроскин продает молоко через магазин и хочет получать за него 500 рублей за литр. Магазин удерживает $20 \%$ стоимости проданного товара. По какой цене будет продаваться молоко в магазине?
7. На складе имеются гвозди в ящиках по $24,23,17$ и 16 кг. Можно ли отправить со склада 100 кг гвоздей, не распечатывая ящики?

1. 431;43
2. 40
3. велосипед
4. 3;4;5;6
5. -
6. 625
7. 4*17+2*16

Решения задач

1. Сумма двух натуральных чисел равна 474. Одно из них оканчивается цифрой $1$. Если эту цифру зачеркнуть, то получится второе число. Найдите эти числа.
   Решение: Пусть первое число имеет вид $10a + 1$, где $a$ — натуральное число. Тогда второе число равно $a$. По условию:
   $10a + 1 + a = 474 \implies 11a = 473 \implies a = 43$.
   Первое число: $10 \cdot 43 + 1 = 431$, второе: $43$.
   Проверка: $431 + 43 = 474$.
   Ответ: 431 и 43.
2. В поход отправились учащиеся $5$-х и $6$-х классов. Мальчиков было 16; шестиклассниц и шестиклассников всего 24; пятиклассниц столько, сколько шестиклассников (мальчиков из 6 класса). Сколько всего детей отправилось в поход?
   Решение:
   Пусть шестиклассников (мальчиков) — $x$, тогда пятиклассниц тоже $x$.
   Шестиклассниц: $24 - x$.
   Пятиклассников (мальчиков): $16 - x$.
   Общее количество детей:
   $x$ (пятиклассницы) + $(16 - x)$ (пятиклассники) + $x$ (шестиклассники) + $(24 - x)$ (шестиклассницы) = $40$.
   Ответ: 40.
3. Что быстрее: проехать весь путь на велосипеде или половину пути проехать на мотоцикле, а вторую половину пройти пешком, если скорость мотоцикла в два раза больше скорости велосипеда, а скорость велосипеда в два раза больше скорости пешехода?
   Решение: Пусть $S$ — весь путь, $v$ — скорость велосипеда. Тогда:
   Время на велосипеде: $\frac{S}{v}$.
   Время на мотоцикле и пешком: $\frac{S/2}{2v} + \frac{S/2}{v/2} = \frac{S}{4v} + \frac{S}{v} \cdot \frac{1}{2} = \frac{3S}{4v}$.
   Так как $\frac{4} <4} < 1$, второй вариант быстрее.
   Ответ: Второй способ быстрее.
4. Даны три прямые. На каждой прямой — две точки. Сколько всего точек? Укажите все варианты.
   Решение: Возможные случаи:
   • Все прямые пересекаются в одной точке: 4 точки.
   • Две прямые параллельны, третья пересекает их: 6 точек.
   • Все прямые параллельны: 6 точек.
   • Попарное пересечение в разных точках: 6 точек.
   Ответ: 4, 5 или 6 точек.
5. -
6. Матроскин продает молоко через магазин и хочет получать за него 500 рублей за литр. Магазин удерживает $20\%$ стоимости проданного товара. По какой цене будет продаваться молоко в магазине?
   Решение: Пусть цена в магазине — $x$ рублей. Матроскин получает $80\%$ от $x$:
   $0,8x = 500 \implies x = \frac{500}{0,8} = 625$ рублей.
   Ответ: 625 рублей.
7. На складе имеются гвозди в ящиках по $24, 23, 17$ и $16$ кг. Можно ли отправить со склада $100$ кг гвоздей, не распечатывая ящики?
   Решение: Подберём комбинацию:
   $17 \cdot 4 + 16 \cdot 2 = 68 + 32 = 100$ кг.
   Ответ: Да, используя 4 ящика по 17 кг и 2 ящика по 16 кг.