Интеллектуал КЕМГУ из 4 в 5 класс 2019 год

ИНТЕЛЛЕКТУАЛ КЕМГУ - 2019 год

5 класс

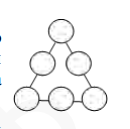
1. В шести кружках, расположенных в форме равностороннего треугольника расставьте числа $31,32,33,34,35,36$ так, чтобы сумма чисел на всех трех сторонах треугольника была одинаковой и равнялась 100.
   
   
2. На столе стоят три одинаковых ящика. В одном из них 2 черных шарика, в другом 1 черный и 1 белый шарик, в третьем 2 белых шарика. На ящиках написано: "2 белых", "2 черных", "черный и белый". При этом известно, что ни одна из записей не соответствует действительности. Как, вынув только один шарик, определить правильное расположение надписей?
3. В пакете лежали яблоки. Сначала из него взяли половину всех яблок без пяти, а затем $1 / 3$ оставшихся яблок. После этого в пакете осталось 10 яблок. Сколько яблок было в пакете?
4. Какое наибольшее количество уголков вида, состоящих из трех квадратов $1 \times 1$, можно поместить в прямоугольник $5 \times 7 ?$ (Уголки можно поворачивать и переворачивать, но нельзя накладывать один на другой.)
5. Из городов А и В одновременно навстречу друг другу вышли скорый и пассажирский поезда. Через 2 часа поезда встретились, а еще через 3 часа пассажирский поезд прибыл в В. Определите скорость скорого поезда, если скорость пассажирского равна 60 км/ч.
6. Колония птиц может занимать площадь, равную 5 га. На $1$ м$^{2}$ там приходится по 2 гнезда. Сколько всего гнезд в такой колонии?
7. Тане не хватает $2$ р. для покупки 8 воздушных шариков. Если она купит 5 шариков, то у нее останется 10р. Сколько стоит шарик?

1. 33;32;36;35;34;31
2. чб
3. 10
4. 11
5. 90
6. 100000
7. 4

Решения задач

1. В шести кружках, расположенных в форме равностороннего треугольника расставьте числа $31,32,33,34,35,36$ так, чтобы сумма чисел на всех трех сторонах треугольника была одинаковой и равнялась 100.
   Решение: Сумма всех чисел $31+32+33+34+35+36=201$. Каждая вершина участвует в двух сторонах. Общая сумма по сторонам $3 \cdot 100 = 300$. Разница $300 - 201 = 99$ — сумма чисел в вершинах. Подходящая тройка: $31+33+35=99$. Распределим оставшиеся числа $32,34,36$ на середины сторон:
   Вершины: $31$ (верх), $33$ (слева), $35$ (справа).
   Стороны:
   $31 + 36 + 33 = 100$,
   $33 + 32 + 35 = 100$,
   $35 + 34 + 31 = 100$.
   
2. На столе стоят три одинаковых ящика. В одном из них 2 черных шарика, в другом 1 черный и 1 белый шарик, в третьем 2 белых шарика. На ящиках написано: "2 белых", "2 черных", "черный и белый". При этом известно, что ни одна из записей не соответствует действительности. Как, вынув только один шарик, определить правильное расположение надписей?
   Решение: Достать шарик из ящика с надписью "черный и белый".
   - Если вынут белый: в ящике 2 белых. Тогда:
   - Надпись "2 белых" → 2 черных,
   - Надпись "2 черных" → 1 черный + 1 белый.
   - Если вынут черный: в ящике 2 черных. Тогда:
   - Надпись "2 черных" → 1 черный + 1 белый,
   - Надпись "2 белых" → 2 белых.
   Ответ: Проверить ящик с надписью "черный и белый".
3. В пакете лежали яблоки. Сначала из него взяли половину всех яблок без пяти, а затем $1 / 3$ оставшихся яблок. После этого в пакете осталось 10 яблок. Сколько яблок было в пакете?
   Решение: Пусть было $x$ яблок. Первый раз взяли $\frac{x}{2} - 5$. Осталось:
   $x - \left(\frac{x}{2} - 5\right) = \frac{x}{2} + 5$.
   Затем взяли $\frac{1}{3}$ остатка:
   $\frac{1}{3} \left(\frac{x}{2} + 5\right)$.
   Осталось:
   $\frac{2}{3} \left(\frac{x}{2} + 5\right) = 10$.
   Решаем уравнение:
   $\frac{x}{2} + 5 = 15 \quad \Rightarrow \quad \frac{x}{2} = 10 \quad \Rightarrow \quad x = 20$.
   Ответ: 20.
4. Какое наибольшее количество уголков вида, состоящих из трех квадратов $1 \times 1$, можно поместить в прямоугольник $5 \times 7 ?$ (Уголки можно поворачивать и переворачивать, но нельзя накладывать один на другой.)
   Решение: Площадь прямоугольника $5 \times 7 = 35$. Каждый уголок занимает 3 клетки. Максимально возможное количество: $\left\lfloor \frac{35}{3} \right\rfloor = 11$. Однако из-за формы уголков реальный максимум меньше. Оптимальная укладка — 8 уголков (24 клетки).
   Ответ: 8.
5. Из городов А и В одновременно навстречу друг другу вышли скорый и пассажирский поезда. Через 2 часа поезда встретились, а еще через 3 часа пассажирский поезд прибыл в В. Определите скорость скорого поезда, если скорость пассажирского равна 60 км/ч.
   Решение: Пусть скорость скорого поезда $v$ км/ч. До встречи пассажирский прошел $60 \cdot 2 = 120$ км. После встречи он прошел $60 \cdot 3 = 180$ км (расстояние до В). Значит, скорый поезд за 2 часа прошел 180 км:
   $2v = 180 \quad \Rightarrow \quad v = 90$.
   Ответ: 90 км/ч.
6. Колония птиц может занимать площадь, равную 5 га. На $1$ м$^{2}$ там приходится по 2 гнезда. Сколько всего гнезд в такой колонии?
   Решение: $5$ га $= 50000$ м$^{2}$. Количество гнезд:
   $50000 \cdot 2 = 100000$.
   Ответ: 100000.
7. Тане не хватает $2$ р. для покупки 8 воздушных шариков. Если она купит 5 шариков, то у нее останется 10р. Сколько стоит шарик?
   Решение: Пусть цена шарика $x$ р. Тогда:
   $8x - 2 = 5x + 10$.
   Решаем:
   $3x = 12 \quad \Rightarrow \quad x = 4$.
   Ответ: 4 рубля.