8 800 707 6729
8 800 707 6729Telegram канал

ФМЛ №30 из 7 в 8 класс 2020 год

Школа:
Сложность:
Дата экзамена: 2020
Школа:
Сложность:
Дата экзамена: 2020
youit.school ©

ЛИЦЕЙ №30 (СПБ)


2020 год


1 тур



  1. Вычислите: $\frac{\left(85 \frac{7}{30}-83 \frac{5}{18}\right): 2 \frac{2}{3}}{0,04} \cdot \frac{3}{11}$.
  2. Разложите на множители: $(a-b)^{2}-b^{2}-c^{2}+2 b c$.
  3. Решите уравнение: $\frac{x-3}{x-1}=\frac{x^{2}-5}{2 x-2}$.
  4. Какие из следующих утверждений верны? Ответ кратко обосновать.
    1. Середина гипотенузы прямоугольного треугольника равноудалена от всех его сторон.
    2. $8^{7}-2^{18}$ делится на $7 .$
    3. Если сторона и три угла одного треугольника равны стороне и трем углам другого треугольника, то такие треугольники равны.
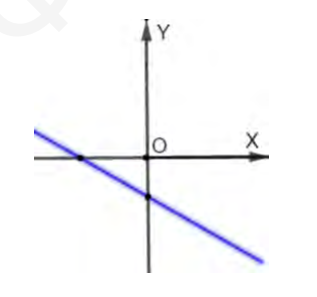
  5. На рисунке изображен график функции $y=k x+d$.
    1. Определите знак коэффициента $d .$
    2. Проходит ли график через точку с координатами $(1 ; d) ?$

  6. Из двух городов А и В, расстояние между которыми равно 600 км, одновременно навстречу друг другу выехали два поезда. Через 2ч 24 мин расстояние между ними стало равным 240 км. С какой скоростью идут поезда, если скорость первого поезда на 14 км/ч больше скорости второго?
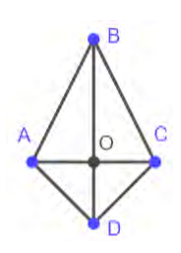
  7. Четырёхугольник $\mathrm{ABCD}$ называется дельтоидом, если в нём $\mathrm{AB}=\mathrm{BC}$ и $\mathrm{AD}=\mathrm{DC}$. Докажите, что точка $\mathrm{O}$ пересечения диагоналей дельтоида является серединой одной из его диагоналей.
  8. Известно, что НОД $(a ; b)=a$, где $a, b$ - натуральные числа. Найдите НОК $(a ; b)$. (НОД $(a ; b)$ - наибольший общий делитель чисел $a$ и $b$, НОК $(a ; b)$ - их наименьшее общее кратное).
  9. Числа от 1 до 37 записаны в строку так, что сумма любых первых нескольких чисел делится на следующее за ними число. Какое число стоит на третьем месте, если на первом месте написано число 37, а на втором - число 1?
Материалы школы Юайти
youit.school ©
Ответы:


  1. 5
  2. $[a-2b+c][a-c]$
  3. нет решений
  4. б
  5. отрицательное;нет
  6. 68;82
  7. b
  8. 2
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите: $\frac{\left(85 \frac{7}{30}-83 \frac{5}{18}\right): 2 \frac{2}{3}}{0,04} \cdot \frac{3}{11}$.
    Решение:
    Переведем смешанные дроби в неправильные:
    $85\frac{7}{30} = \frac{85 \cdot 30 + 7}{30} = \frac{2557}{30}$; $83\frac{5}{18} = \frac{83 \cdot 18 + 5}{18} = \frac{1499}{18}$.
    Найдем разность: $\frac{2557}{30} - \frac{1499}{18} = \frac{2557 \cdot 3 - 1499 \cdot 5}{90} = \frac{7671 - 7495}{90} = \frac{176}{90} = \frac{88}{45}$.
    Разделим на $2\frac{2}{3} = \frac{8}{3}$: $\frac{88}{45} : \frac{8}{3} = \frac{88}{45} \cdot \frac{3}{8} = \frac{11}{15}$.
    Разделим на $0,04$: $\frac{11}{15} : 0,04 = \frac{11}{15} \cdot 25 = \frac{275}{15} = \frac{55}{3}$.
    Умножим на $\frac{3}{11}$: $\frac{55}{3} \cdot \frac{3}{11} = 5$.
    Ответ: 5.

  2. Разложите на множители: $(a-b)^{2}-b^{2}-c^{2}+2 b c$.
    Решение:
    Раскроем квадрат: $(a - b)^2 - b^2 - c^2 + 2bc = a^2 - 2ab + b^2 - b^2 - c^2 + 2bc = a^2 - 2ab - c^2 + 2bc$.
    Сгруппируем: $a^2 - 2ab + (2bc - c^2) = a(a - 2b) + c(2b - c)$.
    Альтернативный подход: $(a - b)^2 - (b^2 + c^2 - 2bc) = (a - b)^2 - (b - c)^2 = (a - b - b + c)(a - b + b - c) = (a - 2b + c)(a - c)$.
    Ответ: $(a - 2b + c)(a - c)$.

  3. Решите уравнение: $\frac{x-3}{x-1}=\frac{x^{2}-5}{2 x-2}$.
    Решение:
    Умножим обе части на $2(x - 1)$: $2(x - 3) = x^2 - 5$.
    Раскроем скобки: $2x - 6 = x^2 - 5$.
    Перенесем все в одну сторону: $x^2 - 2x + 1 = 0$.
    Решим квадратное уравнение: $(x - 1)^2 = 0 \Rightarrow x = 1$.
    Проверим ОДЗ: знаменатель исходного уравнения $x - 1 = 0$ при $x = 1$ обращается в ноль. Решений нет.
    Ответ: нет решений.

  4. Какие из следующих утверждений верны? Ответ кратко обосновать.
    1. Середина гипотенузы прямоугольного треугольника равноудалена от всех его сторон.
      Ответ: Неверно. Середина гипотенузы — центр описанной окружности, равноудалена от. \. \.
    2. $8^{7}-2^{18}$ делится на $7 .$
      Ответ: Верно. $8 \equiv 1 \mod 7 \Rightarrow 8^7 \equiv 1^7 = 1 \mod 7$; $2^3 = 8 \equiv 1 \mod 7 \Rightarrow 2^{18} = (2^3)^6 \equiv 1^6 = 1 \mod 7$. Тогда $8^7 - 2^{18} \equiv 1 - 1 = 0 \mod 7$.
    3. Если сторона и три угла одного треугольника равны стороне и трем углам другого треугольника, то такие треугольники равны.
      Ответ: Неверно. Три угла определяют треугольник с точностью до подобия. Сторона может соответствовать разным углам в треугольниках.

    Ответ: верно только б).

  5. На рисунке изображен график функции $y=k x+d$.
    1. Определите знак коэффициента $d .$
      Ответ: График пересекает ось $y$ ниже нуля $\Rightarrow d < 0$.
    2. Проходит ли график через точку с координатами $(1 ; d) ?$
      Ответ: Подставим $x=1$: $y = k \cdot 1 + d$. Если $y = d$, то $k = 0$, что противоречит наклону графика. Не проходит.

    Ответ: отрицательное; нет.

  6. Из двух городов А и В, расстояние между которыми равно 600 км, одновременно навстречу друг другу выехали два поезда. Через 2ч 24 мин расстояние между ними стало равным 240 км. С какой скоростью идут поезда, если скорость первого поезда на 14 км/ч больше скорости второго?
    Решение:
    Время движения: $2$ ч $24$ мин $= 2,4$ ч.
    Общий пройденный путь: $600 - 240 = 360$ км.
    Пусть скорость второго поезда $x$ км/ч, тогда первого — $x + 14$ км/ч.
    Уравнение: $(x + x + 14) \cdot 2,4 = 360$.
    $2x + 14 = \frac{360}{2,4} = 150$.
    $2x = 136 \Rightarrow x = 68$ км/ч (второй поезд).
    Первый поезд: $68 + 14 = 82$ км/ч.
    Ответ: 68 км/ч; 82 км/ч.

  7. Четырёхугольник $\mathrm{ABCD}$ называется дельтоидом, если в нём $\mathrm{AB}=\mathrm{BC}$ и $\mathrm{AD}=\mathrm{DC}$. Докажите, что точка $\mathrm{O}$ пересечения диагоналей дельтоида является серединой одной из его диагоналей.
    Доказательство:
    Рассмотрим треугольники $\triangle ABC$ и $\triangle ADC$. По условию $AB = BC$, $AD = DC$, $AC$ — общая сторона. Треугольники равны по трём сторонам. Следовательно, $\angle BAC = \angle BCA$ и $\angle DAC = \angle DCA$. Диагональ $AC$ является осью симметрии дельтоида. Диагональ $BD$ пересекает $AC$ в точке $O$. В силу симметрии $BO = OD$, значит $O$ — середина диагонали $BD$.

  8. Известно, что НОД $(a ; b)=a$, где $a, b$ - натуральные числа. Найдите НОК $(a ; b)$.
    Решение:
    Если НОД$(a, b) = a$, то $a$ делит $b$, т.е. $b = a \cdot k$. Тогда НОК$(a, b) = b$.
    Ответ: $b$.

  9. Числа от 1 до 37 записаны в строку так, что сумма любых первых нескольких чисел делится на следующее за ними число. Какое число стоит на третьем месте, если на первом месте написано число 37, а на втором - число 1?
    Решение:
    Первые два числа: 37, 1. Сумма $37 + 1 = 38$ должна делиться на третье число $x$. Возможные $x$: 1, 2, 19, 38. Числа 1 и 37 уже использованы, значит $x = 2$ или 19.
    Проверим $x = 2$: сумма первых трёх чисел $37 + 1 + 2 = 40$ должна делиться на четвёртое число. Возможные делители 40: 4, 5, 8 и т.д. (1 и 2 уже есть).
    При $x = 19$: сумма $37 + 1 + 19 = 57$ должна делиться на четвёртое число 57: 57: 57: 3, 19, 57. Число 19 уже есть, 57 не входит в диапазон. Следовательно, подходит $x = 2$.
    Ответ: 2.
Материалы школы Юайти