8 800 707 6729
8 800 707 6729Telegram канал

Школа № 2007 из 4 в 5 класс 2017 год (вариант 1)

Школа:
Сложность:
Дата экзамена: 2017
Печать
youit.school ©

ШКОЛА № 2007


2017 год



  1. Выполните действия в столбик:
    1. $473 \cdot 958 ;$
    2. $1296814: 239 ;$
    3. $379+13445 ;$
    4. $17374-4859$.
  2. Решите по действиям: $743540-173 \cdot(4175-1390416: 349)$
  3. Расставьте скобки, чтобы равенство было верным:
    1. $323: 17-2+283=300$
    2. $336: 7: 8+4=4$
  4. Сравните:
    1. 3 ч 5 мин 7 с и 8543 с;
    2. 7 м$^{2}$ 50 см$^{2}$ и 705 дм $^{2};$
    3. 2 т 1 ц 354 кг 13000 г и 2467 кг.
  5. На доске было записано некоторое число. Из него вычли 7, умножили на 5 , вычли 6 и разделили на 8. Получилось число 3. Какое число было записано на доске?
  6. Вини Пух съедает бочонок мёда за 10 минут, а Пятачок - за 15. За какое время минут они съедят 7 бочонков мёда, если будут есть одновременно?
  7. В $8.00$ из городов, расположенных на расстоянии 700 км, навстречу друг другу выехали две машины. Они встретились в $22.00$ того же дня. Найдите скорость второй машины, если скорость первой 23 км/ч.
  8. В бутылке было 250 мл молока. В первый день Паша выпил пятую часть всего молока. Во второй день он выпил четвертую часть того, что осталось. Все остальное допила Оля. Кто выпил больше молока и насколько?
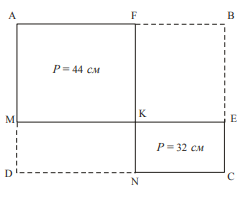
  9. Прямоугольник $ABCD$ разделили двумя прямолинейными разрезами на четыре прямоугольника. Известно, что периметр прямоугольника $AFKM$ равен 44 см, а периметр прямоугольника $KECN$ равен 32 см. Найдите периметр прямоугольника $ABCD$. Ответ объясните.
  10. Квадрат площадью 25 см$^{2}$ разрезали на два прямоугольника. Периметр первого 12 см. Найдите площадь второго прямоугольника.
Материалы школы Юайти
youit.school ©
Ответы:


  1. 453134; 5426; 13824; 12515
  2. 710497
  3. (323:17-2)+283=300; 336:8:(8+4)=4
  4. >; <; =
  5. 13
  6. 42
  7. 27
  8. Оля, на 50
  9. 76
  10. 20
Материалы школы Юайти
youit.school ©
  1. Задача. Выполнить вычисления: $473\cdot 958$, $1296814:239$, $379+13445$, $17374-4859$.
    Решение. Умножим: $473\cdot 958=473\cdot(900+50+8)=473\cdot 900+473\cdot 50+473\cdot 8=425700+23650+3784=453134$. Деление проверим умножением: $1296814:239=5426$, так как $239\cdot 5426=1296814$. Сложение: $13445+379=13824$. Вычитание: $17374-4859=12515$.
    Ответ. $453134;\ 5426;\ 13824;\ 12515$.
  2. Задача. Вычислить по действиям: $743540-173\cdot(4175-1390416:349)$.
    Решение. Сначала делим: $1390416:349=3984$ (так как $349\cdot 3984=1390416$). Затем $4175-3984=191$. Умножаем: $173\cdot 191=173\cdot(200-9)=34600-1557=33043$. Теперь $743540-33043=710497$.
    Ответ. $710497$.
  3. Задача. Расставить скобки, чтобы равенства были верными: $323:17-2+283=300$ и $336:7:8+4=4$.
    Решение. В первом равенстве нужно сначала выполнить деление и вычитание, а потом прибавить $283$: $(323:17-2)+283=300$, так как $323:17=19$, $19-2=17$, $17+283=300$. Во втором равенстве сложение должно быть в скобках, а деления выполняются слева направо: $336:7:(8+4)=4$, так как $8+4=12$, $336:7=48$, $48:12=4$.
    Ответ. $(323:17-2)+283=300;\ 336:7:(8+4)=4$.
  4. Задача. Сравнить величины: 1) $3$ ч $5$ мин $7$ с и $8543$ с; 2) $7$ м$^{2}$ $50$ см$^{2}$ и $705$ дм$^{2}$; 3) $2$ т $1$ ц $354$ кг $13000$ г и $2467$ кг.
    Решение. 1) $3$ ч $5$ мин $7$ с $=3\cdot 3600+5\cdot 60+7=10800+300+7=11107$ с, значит $11107>8543$. 2) Переведём в см$^{2}$: $7$ м$^{2}$ $50$ см$^{2}=7\cdot 10000+50=70050$ см$^{2}$, а $705$ дм$^{2}=705\cdot 100=70500$ см$^{2}$, значит $70050<70500$. 3) Переведём в кг: $2$ т $1$ ц $354$ кг $13000$ г $=2000+100+354+13=2467$ кг, значит величины равны.
    Ответ. $>$; $<$; $=$.
  5. Задача. Из некоторого числа вычли $7$, умножили на $5$, вычли $6$ и разделили на $8$, получилось $3$. Найти исходное число.
    Решение. Выполним обратные действия, начиная с результата $3$. Умножим на $8$: $3\cdot 8=24$. Прибавим $6$: $24+6=30$. Разделим на $5$: $30:5=6$. Прибавим $7$: $6+7=13$.
    Ответ. $13$.
  6. Задача. Вини Пух съедает бочонок мёда за $10$ минут, а Пятачок за $15$ минут. За сколько минут они съедят $7$ бочонков, если едят одновременно?
    Решение. За $30$ минут Вини Пух съест $30:10=3$ бочонка, а Пятачок $30:15=2$ бочонка, вместе $5$ бочонков за $30$ минут. Тогда на $1$ бочонок у них уходит $30:5=6$ минут. На $7$ бочонков нужно $7\cdot 6=42$ минуты.
    Ответ. $42$ минуты.
  7. Задача. В $8.00$ из двух городов на расстоянии $700$ км навстречу друг другу выехали две машины и встретились в $22.00$ того же дня. Скорость первой $23$ км/ч. Найти скорость второй машины.
    Решение. В пути было $22-8=14$ часов. Первая машина проехала $23\cdot 14=322$ км. Тогда вторая машина проехала $700-322=378$ км. Её скорость равна $378:14=27$ км/ч.
    Ответ. $27$ км/ч.
  8. Задача. В бутылке было $250$ мл молока. В первый день Паша выпил $\frac{1}{5}$ всего молока, во второй день выпил $\frac{1}{4}$ того, что осталось. Остальное допила Оля. Кто выпил больше и на сколько?
    Решение. В первый день Паша выпил $250:5=50$ мл, осталось $250-50=200$ мл. Во второй день Паша выпил $200:4=50$ мл. Всего Паша выпил $50+50=100$ мл, значит Оля выпила $250-100=150$ мл. Разница $150-100=50$ мл.
    Ответ. Оля, на $50$ мл.
  9. Условие. Прямоугольник $ABCD$ разрезали двумя прямыми на четыре прямоугольника. Периметр прямоугольника $AFKM$ равен $44$ см, а периметр прямоугольника $KECN$ равен $32$ см. Найти периметр прямоугольника $ABCD$ и объяснить ответ.
    Дано. $P_{AFKM}=44$ см, $P_{KECN}=32$ см. Найти $P_{ABCD}$.
    Решение. Пусть стороны прямоугольника $AFKM$ равны $AF$ и $AM$. Тогда $P_{AFKM}=2(AF+AM)=44$, значит $AF+AM=22$. Пусть стороны прямоугольника $KECN$ равны $KE$ и $EC$. Тогда $P_{KECN}=2(KE+EC)=32$, значит $KE+EC=16$. Весь прямоугольник имеет ширину $AB=AF+KE$ (левая часть и правая часть по разрезу) и высоту $BC=AM+EC$ (верхняя часть и нижняя часть). Тогда $AB+BC=(AF+KE)+(AM+EC)=(AF+AM)+(KE+EC)=22+16=38$, поэтому $P_{ABCD}=2(AB+BC)=2\cdot 38=76$ см.
    Ответ. $76$ см.
  10. Условие. Квадрат площадью $25$ см$^{2}$ разрезали на два прямоугольника. Периметр первого прямоугольника $12$ см. Найти площадь второго прямоугольника.
    Дано. $S=25$ см$^{2}$, $P_{1}=12$ см. Найти $S_{2}$.
    Решение. Площадь квадрата равна произведению его стороны на себя, значит сторона квадрата $5$ см, потому что $5\cdot 5=25$. При разрезании на два прямоугольника один размер каждого прямоугольника равен $5$ см. Пусть второй размер первого прямоугольника равен $x$ см, тогда $P_{1}=2(5+x)=12$, значит $5+x=6$ и $x=1$. Площадь первого прямоугольника $S_{1}=5\cdot 1=5$ см$^{2}$. Тогда площадь второго прямоугольника $S_{2}=25-5=20$ см$^{2}$.
    Ответ. $20$ см$^{2}$.
Материалы школы Юайти