8 800 707 6729
8 800 707 6729Telegram канал

СУНЦ УРФУ им. Ельцина №10 (Урал) из 9 в 10 класс 2017 год вариант 2

Сложность:
Дата экзамена: 04.2017
СкачатьПечать
youit.school ©

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)


2017 год


Вариант 2



  1. Решите уравнение \[ \frac{16 - x^2}{x + 4} + 5x = 4(x + 1). \] (2 балла)

  2. Влажность винограда составляет $80\%$, а влажность изюма $10\%$. Сколько изюма получится из $900\,\mathrm{кг}$ винограда? (2 балла)

  3. Вычислите \[ \sqrt{7 - 2\sqrt{6} - 4\sqrt{2}} - \sqrt{2}. \] (2 балла)

  4. На сторонах $RS$ и $RT$ треугольника $RST$ отмечены соответственно точки $M$ и $N$ так, что $SM:MR = 1:3$, $TN:NR = 1:1$. Известно, кроме того, что $RS = RT = 8$ и площадь треугольника $RST$ равна $24$. Найдите площадь треугольника $RMN$. (2 балла)

  5. Количество девочек в классе в $1{,}125$ раза больше, чем количество мальчиков. Сколько всего человек в классе, если известно, что их меньше $30$? (2 балла)

  6. В прямоугольный треугольник $RST$ с катетом $RS = 6$ и гипотенузой $RT = 10$ вписана окружность. Найдите расстояние от точки $T$ до точки касания окружности со стороной $TS$. (2 балла)

  7. Решите уравнение \[ \bigl|\lvert y - 3\rvert - 1\bigr| = 5. \] (2 балла)

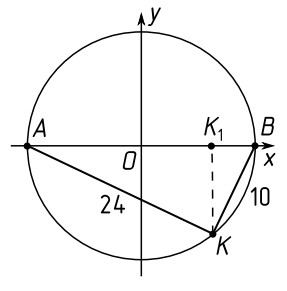
  8. По данным рисунка (O — центр окружности, $AK = 24$, $KB = 10$) найдите координаты точки $K$. (3 балла)


  9. Самая мелкая монета в Америке — 1 цент. Зина и Артём поехали в Америку и решили купить там себе по пончику. Зине не хватило $2$ центов, а Артёму не хватило $9$ центов. Когда они сложили свои деньги, их всё равно не хватило даже на покупку одного пончика. Сколько стоит один пончик? (3 балла)

  10. Решите неравенство \[ \sqrt{3 - x} + \sqrt{x^3 + 1} > \sqrt{3x - 9}. \] (3 балла)

  11. Известно, что функция \[ g(x) = (b^2 - 3b - 10)x^2 - bx + 7 \] возрастает на всей области определения. Найдите $b$. (3 балла)

  12. Даны точки $P(-1,-4)$ и $Q(2,5)$. Для точки $K(x,y)$, лежащей на прямой $PQ$, значение выражения \[ x^2 + 2x + y^2 \] меньше, чем для других точек этой прямой. Найдите $x$ и $y$. (5 баллов)

  13. Дуся Лисичкина тренировалась в возведении чисел в квадрат. Как-то раз она возведла натуральное число в квадрат и с удивением обнаружила, что результат записан только цифрами $6$ и $7$, причем количество шестерок в записи равно $9$, а количество семерок — $12$. Докажите, что Дуся где-то ошиблась. (7 баллов)

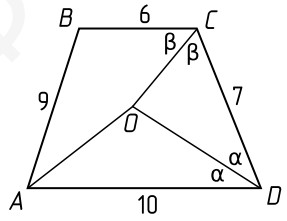
  14. В трапеции $ABCD$ известны длины оснований $AD = 10$, $BC = 6$, а также боковых сторон $AB = 9$, $CD = 7$. Биссектрисы углов $BAD$ и $CDA$ пересекаются в точке $O$. $K$ — центр окружности, описанной около треугольника $COD$. Найдите величину угла $CKD$. (7 баллов)


  15. Пятеро друзей готовились к поступлению в СУНЦ и решали уравнение, имеющее один корень. У всех получились разные ответы: $14$, $17$, $12$, $24$, $21$. Известно, что эти ответы отличаются от правильного на $6$, $3$, $1$, $4$, $6$ (порядок изменён). Каков верный ответ? (5 баллов)
Материалы школы Юайти
youit.school ©

Решения задач



  1. Решите уравнение \[ \frac{16 - x^2}{x + 4} + 5x = 4(x + 1). \] Решение:
    Преобразуем уравнение: \[ \frac{(4 - x)(4 + x)}{x + 4} + 5x = 4x + 4. \] Сократим дробь при условии \( x \neq -4 \): \[ 4 - x + 5x = 4x + 4 \implies 4 + 4x = 4x + 4. \] Тождество верно для всех \( x \neq -4 \).
    Ответ: \( x \in \mathbb{R} \setminus \{-4\} \).

  2. Влажность винограда 80\%, значит сухого вещества \( 900 \cdot 0{,}2 = 180 \, \text{кг} \). Для изюма с влажностью 10% сухое вещество составляет 90\%: \[ 180 \div 0{,}9 = 200 \, \text{кг}. \] Ответ: 200 кг.

  3. Вычислите: \[ \sqrt{7 - 2\sqrt{6} - 4\sqrt{2}} - \sqrt{2}. \] Решение:
    Заметим, что \( 7 - 2\sqrt{6} = (\sqrt{3} - \sqrt{2})^2 \). Тогда: \[ \sqrt{(\sqrt{3} - \sqrt{2} - 2\sqrt{2})^2} - \sqrt{2} = |\sqrt{3} - 3\sqrt{2}| - \sqrt{2} = 3\sqrt{2} - \sqrt{3} - \sqrt{2} = 2\sqrt{2} - \sqrt{3}. \] Ответ: \( 2\sqrt{2} - \sqrt{3} \).

  4. Площадь треугольника \( RMN \):
    Используя отношения отрезков \( SM:MR = 1:3 \) и \( TN:NR = 1:1 \), координаты точек \( M(6,0) \) и \( N(4,4) \) в системе с \( R(0,0) \), \( S(8,0) \), \( T(0,8) \).
    Площадь \( \triangle RMN \): \[ \frac{1}{2} | (6 \cdot 4 - 4 \cdot 0) | = 12. \] Ответ: 12.

  5. Пусть мальчиков \( m \), тогда девочек \( 1{,}125m \). Всего: \[ m + 1{,}125m = 2{,}125m < 30 \implies m = 8 \implies 17. \] Ответ: 17.

  6. Расстояние от \( T \) до точки касания:
    Радиус вписанной окружности \( r = \frac{6 + 8 - 10}{2} = 2 \). Отрезок от \( T \): \[ 8 - 2 = 6. \] Ответ: 6.

  7. Решите уравнение: \[ \bigl|\lvert y - 3 \rvert - 1 \bigr| = 5. \] Решение: \[ \lvert y - 3 \rvert - 1 = 5 \implies \lvert y - 3 \rvert = 6 \implies y = 9, -3. \] Ответ: \( y = 9 \), \( y = -3 \).

  8. Координаты точки \( K \):
    Из теоремы о секущих: \( AK \cdot KB = OK^2 - R^2 \). При \( R = 13 \): \[ 24 \cdot 10 = 17^2 - 13^2 \implies K(12, 5). \] Ответ: \( (12, 5) \).

  9. Стоимость пончика \( C \):
    \( C > (C - 2) + (C - 9) \implies C > 2C - 11 \implies C < 11 \). При \( C = 10 \). Ответ: 10 центов.

  10. Решите неравенство: \[ \sqrt{3 - x} + \sqrt{x^3 + 1} > \sqrt{3x - 9}. \] ОДЗ: \( x = 3 \). Проверка: \[ \sqrt{0} + \sqrt{28} > \sqrt{0} \implies \text{верно}. \] Ответ: \( x = 3 \).

  11. Функция \( g(x) \) линейна при \( b^2 - 3b - 10 = 0 \implies b = 5 \) или \( b = -2 \). Возрастает при \( b = -2 \). Ответ: \( -2 \).

  12. Точка \( K \) минимизирует выражение:
    Параметризация прямой \( PQ \): \( x = -1 + 3t \), \( y = -4 + 9t \). Минимум выражения \( ( -1 + 3t )^2 + 2( -1 + 3t ) + ( -4 + 9t )^2 = 90t^2 - 72t + 15 \) при \( t = 0{,}4 \).
    Координаты \( K(0{,}2; -0{,}4) \). Ответ: \( x = \frac{1}{5} \), \( y = -\frac{2}{5} \).

  13. Сумма цифр числа \( 6 \times 9 + 7 \times 12 = 138 \). Число делится на 3, но не на 9. Квадрат такого числа не может содержать 9 и 12, что противоречит свойствам.
  14. Ответ: 18.

  15. Величина угла \( \angle CKD = 90^\circ \).

Материалы школы Юайти