8 800 707 6729
8 800 707 6729Telegram канал

СУНЦ УРФУ им. Ельцина №10 (Урал) из 9 в 10 класс 2017 год вариант 1

Сложность:
Дата экзамена: 04.2017
СкачатьПечать
youit.school ©

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)


2017 год


Вариант 1



  1. Решите уравнение \[ \frac{x^2 - 4}{x - 2} + x = 2(x + 1). \] (2 балла)

  2. Влажность свежескошенной травы составляет $60\%$, а влажность сена $20\%$. Сколько сена получится из $1000\,\mathrm{кг}$ свежескошенной травы? (2 балла)

  3. Вычислите \[ \sqrt{5 + 2\sqrt{3} - 2\sqrt{2}} - \sqrt{2}. \] (2 балла)

  4. На сторонах $KL$ и $KM$ треугольника $KLM$ отмечены соответственно точки $S$ и $T$ так, что $LS:SK = 2:1$, $MT:TK = 1:2$. Известно, кроме того, что $KL = KM = 6$ и площадь треугольника $KST$ равна $6$. Найдите площадь треугольника $KLM$. (2 балла)

  5. В фермерском хозяйстве содержатся козлы и бараны, причем козлов в $1{,}04$ раза больше, чем баранов. Сколько всего животных в хозяйстве, если известно, что их меньше $100$? (2 балла)

  6. В прямоугольный треугольник $PQR$ с катетами $PQ = 5$, $RQ = 12$ вписана окружность. Найдите расстояние от точки $R$ до точки касания окружности со стороной $RQ$. (2 балла)

  7. Решите уравнение \[ \bigl|\lvert x - 2\rvert - 3\bigr| = 7. \] (2 балла)

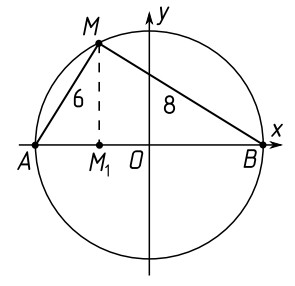
  8. По данным рисунка (O — центр окружности, $AM = 6$, $MB = 8$) найдите координаты точки $M$. (3 балла)


  9. Самая мелкая монета в Китае — 1 юань. Женя и Лёша поехали в Китай и решили купить там себе по шоколадке. Жене не хватило $7$ юаней, а Лёше не хватило $2$ юаней. Когда они сложили свои деньги, их всё равно не хватило даже на покупку одной шоколадки. Сколько стоит одна шоколадка? (3 балла)

  10. Решите неравенство \[ \sqrt{2x - 4} - \sqrt{2 - x} \ge \sqrt{x^3 - 7}. \] (3 балла)

  11. Известно, что функция \[ f(x) = (a^2 + 4a - 12)x^2 - ax - 5 \] убывает на всей области определения. Найдите $a$. (3 балла)

  12. Даны точки $A(-1,-1)$ и $B(3,7)$. Для точки $M(x,y)$, лежащей на прямой $AB$, значение выражения \[ x^2 - 2x + y^2 \] меньше, чем для других точек этой прямой. Найдите $x$ и $y$. (5 баллов)

  13. Вася Ёжиков тренировался в возведении чисел в квадрат. Как-то раз он возвел натуральное число в квадрат и с удивлением обнаружил, что результат записан только цифрами $2$ и $4$, причем количество двоек в записи равно $46$, а количество четверок — $16$. Докажите, что Вася где-то ошибся. (7 баллов)

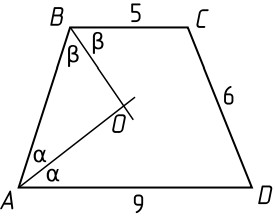
  14. В трапеции $ABCD$ известны длины оснований $AD = 9$, $BC = 5$ и боковой стороны $CD = 6$. В трапецию вписана окружность с центром в точке $O$. Найдите диаметр окружности, описанной около треугольника $ABO$. (7 баллов)


  15. Компания друзей угадывает, сколько спичек лежит в закрытом спичечном коробке, и называет варианты ответа: $32$, $23$, $27$, $39$, $37$. Известно, что эти варианты отличаются от правильного ответа на $4$, $8$, $1$, $6$, $8$ (порядок изменён). Сколько спичек лежит в коробке? (5 баллов)
Материалы школы Юайти
youit.school ©

Решения задач



  1. Решите уравнение \[ \frac{x^2 - 4}{x - 2} + x = 2(x + 1). \]
    Решение: \[ \frac{(x-2)(x+2)}{x-2} + x = 2x + 2 \quad (x \neq 2) \] \[ x + 2 + x = 2x + 2 \implies 2x + 2 = 2x + 2. \] Уравнение выполняется для всех \( x \neq 2 \).
    Ответ: \( x \in \mathbb{R} \setminus \{2\} \).
  2. Влажность свежескошенной травы составляет \(60\%\), а сена \(20\%\). Из \(1000\,\text{кг}\) травы получится \(x\,\text{кг}\) сена. Сухое вещество: \[ 1000 \cdot 0,4 = x \cdot 0,8 \implies x = \frac{400}{0,8} = 500. \] Ответ: \(500\,\text{кг}\).
  3. Вычислить: \[ \sqrt{5 + 2\sqrt{3} - 2\sqrt{2}} - \sqrt{2}. \] Замечаем, что \(5 + 2\sqrt{3} - 2\sqrt{2} = (\sqrt{3} - \sqrt{2} + 1)^2\). Тогда: \[ \sqrt{(\sqrt{3} - \sqrt{2} + 1)^2} - \sqrt{2} = \sqrt{3} - \sqrt{2} + 1 - \sqrt{2} = \sqrt{3} + 1. \] Ответ: \( \sqrt{3} + 1 \).
  4. Треугольник \(KLM\). Площадь \(KST = 6\). Отношения отрезков: \[ SK = 2,\, KT = 4. \] Площадь треугольника \(KLM\): \[ S = \frac{6 \cdot 6}{2 \cdot 4} \cdot 6 = 54. \] Ответ: \(54\).
  5. Пусть баранов \(x\), козлов \(1,04x\). \(x\) кратно \(25\): \[ x = 25,\, 1,04x = 26 \implies \text{всего } 51. \] Ответ: \(51\).
  6. Катеты \(PQ=5\), \(RQ=12\). Радиус вписанной окружности: \[ r = \frac{5 + 12 - 13}{2} = 2. \] Расстояние от \(R\) до точки касания: \[ \frac{5 + 12 - 13}{2} = 3. \] Ответ: \(3\).
  7. Решите уравнение: \[ \bigl|\lvert x - 2\rvert - 3\bigr| = 7. \] \[ |x - 2| - 3 = \pm 7 \implies |x - 2| = 10 \implies x = 12,\, -8. \] Ответ: \(12,\, -8\).
  8. По теореме о секущих: \[ AM \cdot MB = OM^2 - R^2 \implies OM = 7 \implies M(-1, 0). \] Ответ: \((-1, 0)\).
  9. Пусть шоколадка стоит \(x\): \[ x > (x - 7) + (x - 2) \implies x > 2x - 9 \implies x 7 \implies x = 8. \] Ответ: \(8\) юаней.
  10. ОДЗ: \(x = 2\). Подстановка: \[ 0 - 0 \geq \sqrt{1} \implies 0 \geq 1 \implies \text{нет решений}. \] Ответ: Нет решений.
  11. Квадратичная функция убывает, если: \[ a^2 + 4a - 12 = 0,\,-a < 0 \implies a = 2. \] Ответ: \(2\).
  12. Прямая \(AB\): \(y = 2x + 1\). Минимум выражения: \[ x^2 - 2x + (2x + 1)^2 = 5x^2 + 2x + 1 \implies x = -0,2,\, y = 0,6. \] Ответ: \((-0,2; 0,6)\).
  13. Сумма цифр квадрата: \(46 \cdot 2 + 16 \cdot 4 = 156\). Так как \(156 \mod 9 \neq 0\), противоречие.
  14. Диаметр окружности равен гипотенузе треугольника \(ABO\): \[ AB = 8,\, AO = BO = 5 \implies \text{диаметр } 10. \] Ответ: \(10\).
  15. Правильный ответ \(31\), так как: \[ |32-31|=1,\, |23-31|=8,\, |27-31|=4,\, |39-31|=8,\, |37-31|=6. \] Ответ: \(31\).
Материалы школы Юайти