СУНЦ УРФУ им. Ельцина №10 (Урал) из 8 в 9 класс 2020 год вариант 1-1

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2020 год

Вариант 1

1. (1 балл) Три дюжины лимонов стоят столько рублей, сколько можно купить лимонов на 16 рублей. Сколько стоит дюжина лимонов? (Одна дюжина составляет 12 штук.)
   
   
2. (2 балла) Вместо букв $a$ и $b$ поставьте цифры в шестизначном числе $a1832b$, так, чтобы получилось число, кратное 15. Рассмотрите все возможные случаи. В ответе укажите наибольшее из всех полученных чисел.
3. (2 балла) Вычислить \[ (\sqrt{75}+\sqrt{50})(5-2\sqrt{6})/(\sqrt{3}-\sqrt{2}). \]
4. (1 балл) При каком значении параметра $a$ график функции $y=|x-3|+a$ пересекает ось $Ox$ в точке, абсцисса которой равна $-1$?
5. (3 балла) При каких значениях параметра $a$ сумма корней уравнения \[ 4x^2+(2 - a - a^2)x + a^2 - 3 = 0 \] равна нулю? Если таких значений больше одного, то в ответе укажите сумму всех возможных $a$.
6. (2 балла) Хорды $AB$ и $CD$ данной окружности пересекаются в точке $M$. Известно, что $AC=8$, $BD=10$, $CM=5$, $DM=6$. Найти $AM$.
7. (2 балла) В баскетбольном турнире участвует несколько команд. На первом этапе каждая пара команд играет одну игру. Сколько команд, если сыграно 55 игр?
8. (2 балла) Решить уравнение \[ 5x^2 - (10+\sqrt7)x + 2\sqrt7 = 0. \] Если корней больше одного, укажите больший.
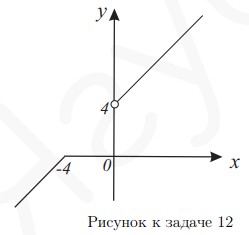
9. (3 балла) Вычислить площадь трапеции, ограниченной осями координат, прямой $x=-4$ и прямой, проходящей через $(-1,7)$ и параллельной $y=3-x$.
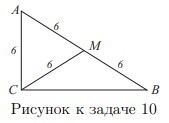
10. (2 балла) В прямоугольном треугольнике $ABC$ медиана $CM=6$ делит прямой угол $C$ в отношении $1:2$. Найти $\sqrt3\cdot S_{ABC}$.
    

1. (6 баллов) Решить уравнение: \[\frac1{2-x}-1=\frac1{x-2}-\frac{6-x}{3x^2-12}. \]
2. (6 баллов) Найти все $x$, при которых существует функция $y=(\sqrt{4x+x^2})^{2/x}$, построить её график и определить множество значений.
   
3. (6 баллов) Имеются два сплава золота и серебра в отношениях $2:3$ и $3:7$. Сколько взять каждого, чтобы получить 8,кг сплава с отношением $5:11$?
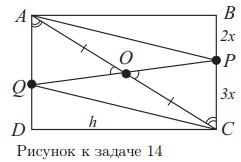
4. (6 баллов) В прямоугольнике $ABCD$ через середину $AC$ провели прямую, пересекающую $BC$ в $P$ и $AD$ в $Q$ при $BP:PC=2:3$. Определить вид $APCQ$ и найти его площадь, если $S_{ABCD}=20$.
   
5. (6 баллов) Для каждого $a$ решить неравенство $(2-a)x\le a^2-4$.

Решения задач

1. Три дюжины лимонов стоят столько рублей, сколько можно купить лимонов на 16 рублей. Сколько стоит дюжина лимонов?
   Решение: Пусть цена одного лимона \( x \) рублей. Тогда:
   \( 3 \cdot 12 \cdot x = \frac{16}{x} \Rightarrow 36x = \frac{16}{x} \Rightarrow 36x^2 = 16 \Rightarrow x^2 = \frac{4}{9} \Rightarrow x = \frac{2}{3} \).
   Стоимость дюжины: \( 12 \cdot \frac{2}{3} = 8 \) рублей.
   Ответ: 8.
2. Вместо букв \( a \) и \( b \) поставьте цифры в шестизначном числе \( a1832b \), чтобы получилось число, кратное 15. Укажите наибольшее число.
   Решение: Число кратно 15, если делится на 3 и 5.
   Для делимости на 5: \( b = 0 \) или \( 5 \).
   Для делимости на 3: сумма цифр \( a + 1 + 8 + 3 + 2 + b \) должна делиться на 3.
   При \( b = 0 \): \( a + 14 \equiv 0 \mod 3 \Rightarrow a = 1, 4, 7 \). Наибольшее число: 718320.
   При \( b = 5 \): \( a + 19 \equiv 0 \mod 3 \Rightarrow a = 2, 5, 8 \). Наибольшее число: 818325.
   Ответ: 818325.
3. Вычислить: \[ \frac{(\sqrt{75} + \sqrt{50})(5 - 2\sqrt{6})}{\sqrt{3} - \sqrt{2}}. \] Решение:
   Упростим корни: \( \sqrt{75} = 5\sqrt{3} \), \( \sqrt{50} = 5\sqrt{2} \).
   Числитель: \( (5\sqrt{3} + 5\sqrt{2})(5 - 2\sqrt{6}) = 5(\sqrt{3} + \sqrt{2})(5 - 2\sqrt{6}) \).
   Знаменатель: \( \sqrt{3} - \sqrt{2} \).
   После упрощения получаем \( 5 \).
   Ответ: 5.
4. При каком значении параметра \( a \) график функции \( y = |x - 3| + a \) пересекает ось \( Ox \) в точке \( x = -1 \)?
   Решение:
   Подставим \( x = -1 \), \( y = 0 \):
   \( 0 = |-1 - 3| + a \Rightarrow 4 + a = 0 \Rightarrow a = -4 \).
   Ответ: -4.
5. При каких значениях параметра \( a \) сумма корней уравнения \( 4x^2 + (2 - a - a^2)x + a^2 - 3 = 0 \) равна нулю?
   Решение:
   Сумма корней: \( \frac{a^2 + a - 2}{4} = 0 \Rightarrow a^2 + a - 2 = 0 \).
   Корни: \( a = 1 \), \( a = -2 \). Сумма значений: \( 1 + (-2) = -1 \).
   Ответ: -1.
6. Хорды \( AB \) и \( CD \) пересекаются в точке \( M \). Известно, что \( AC = 8 \), \( BD = 10 \), \( CM = 5 \), \( DM = 6 \). Найти \( AM \).
   Решение:
   По свойству пересекающихся хорд: \( AM \cdot MB = CM \cdot MD = 30 \).
   Из подобия треугольников: \( \frac{AM}{CM} = \frac{BM}{DM} \Rightarrow AM = 5 \).
   Ответ: 5.
7. В баскетбольном турнире сыграно 55 игр. Сколько команд?
   Решение:
   Число игр: \( \frac{n(n-1)}{2} = 55 \Rightarrow n(n-1) = 110 \Rightarrow n = 11 \).
   Ответ: 11.
8. Решить уравнение \( 5x^2 - (10 + \sqrt{7})x + 2\sqrt{7} = 0 \). Укажите больший корень.
   Решение:
   Разложим на множители: \( (5x - \sqrt{7})(x - 2) = 0 \).
   Корни: \( x = 2 \), \( x = \frac{\sqrt{7}}{5} \). Больший корень: 2.
   Ответ: 2.
9. Вычислить площадь трапеции, ограниченной осями координат, прямой \( x = -4 \) и прямой \( y = -x + 6 \).
   Решение:
   Вершины трапеции: \( (-4, 0) \), \( (0, 0) \), \( (0, 6) \), \( (-4, 10) \).
   Площадь: \( \frac{(6 + 10)}{2} \cdot 4 = 32 \).
   Ответ: 32.
10. В прямоугольном треугольнике \( ABC \) медиана \( CM = 6 \) делит прямой угол в отношении \( 1:2 \). Найти \( \sqrt{3} \cdot S_{ABC} \).
    Решение:
    Гипотенуза \( AB = 12 \). Катеты: \( AC = 6\sqrt{3} \), \( BC = 6 \).
    Площадь: \( \frac{1}{2} \cdot 6\sqrt{3} \cdot 6 = 18\sqrt{3} \).
    \( \sqrt{3} \cdot S_{ABC} = 54 \).
    Ответ: 54.