СУНЦ УРФУ им. Ельцина №10 (Урал) из 8 в 9 класс 2020 год вариант 1

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2020 год

Вариант 1

1. (2 балла) Из одной точки проведены четыре луча \(OA\), \(OB\), \(OC\) и \(OD\). Известны величины углов: \(\angle AOB = 10^\circ\), \(\angle BOC = 20^\circ\), \(\angle COD = 40^\circ\). Найдите сумму всевозможных значений углов \(AOD\) (в градусах).
2. (2 балла) В школе 9 класс закончили более 300 учеников. Только 40% из них решили пойти в 10 класс. Их осталось менее двухсот. Из не бросивших школу 20% были мальчики, и лишь 15% девочек выбрали физико-математический класс. Сколько всего учеников закончили 9 класс?
3. (2 балла) Найдите периметр трапеции, если ее диагональ равна 17, боковые стороны равны 10, а одно основание на 12 меньше другого.
4. (3 балла) При каком значении \(a\) наименьшее значение выражения \[ x^2 - 8x - 2a - 1 \] равно 7?
5. (3 балла) Вычислите \[ \Bigl(\tfrac{12}{\sqrt{13}-1} + \tfrac{6}{\sqrt{13}-2} + \tfrac{4}{\sqrt{13}-3}\Bigr)\;\cdot\;\tfrac{3}{\sqrt{13}+2}. \]
6. (3 балла) На \(n\) карточках написали все натуральные числа от 1 до \(n\). После этого карточки перевернули и на обратной стороне написали разность \(n\) и числа на противоположной стороне. Оказалось, что сумма цифр на обеих сторонах каждой карточки равна 12. Найдите \(n\).
7. (3 балла) Найдите сумму всех целых \(x\), удовлетворяющих неравенству \[ \sqrt{x+8}\;(x^2 + 5x - 6) \le 0. \]
8. (3 балла) Сколько чисел \(x\), делящихся на 7, удовлетворяют неравенству \[ |x+1| + |x+90| \le 89\,? \]
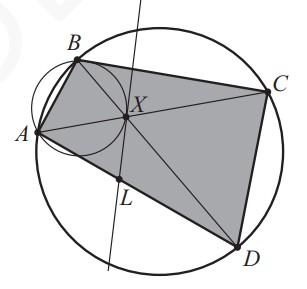
9. (4 балла) Дан вписанный четырёхугольник $ABCD$. Его диагонали пересекаются в точке $X$. Вокруг треугольника $ABX$ описали окружность. Через точку $X$ провели касательную к этой окружности, которая пересекает $AD$ в точке $L$. Найдите сумму (в градусах) углов $LXC$ и $XCD$, если $\angle ABD = 55^\circ$, $\angle BAC = 44^\circ$.
   

2. (5 баллов) При каких значениях параметра \(a\) точка пересечения прямых \[ y = x - 4 \quad\text{и}\quad y = -x + a \] расположена выше оси абсцисс, но ниже прямой \[ y = -2x + 15\,? \]
3. (6 баллов) Вступительный экзамен состоит из двух частей. Даша наугад расставила ответы. Затем Маша проверила ответы и часть неправильных изменила. После исправлений Маши количество неверных ошибок в первой части оказалось в пределах от 15,5% до 18% от числа неправильных ответов в первой части изначально. При этом количество неправильных ответов во второй части уменьшилось втрое и составило 25% от числа неправильных ответов в первой части до исправления. Какое наименьшее число неправильных ответов могла дать Даша?
4. (6 баллов) В выпуклом четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны. На стороне \(BC\) отмечена такая точка \(E\), что \[ \angle BAD + \angle CDE = \angle EDA. \] Из точки \(E\) на сторону \(AD\) опущен перпендикуляр \(EF\). Докажите, что \[ BC + FD > AF. \]
5. (8 баллов) Найти наибольшее возможное значение суммы \(x + y\), если \(x\) и \(y\) целые и выполнено неравенство \[ 4\bigl|4x + 5y - 2\bigr| \;\le\; 3 - 2\sqrt{3x + 4y - 3}. \]

Решения задач

1. Из одной точки проведены четыре луча \(OA\), \(OB\), \(OC\) и \(OD\). Известны величины углов: \(\angle AOB = 10^\circ\), \(\angle BOC = 20^\circ\), \(\angle COD = 40^\circ\). Найдите сумму всевозможных значений углов \(AOD\) (в градусах).
   Решение: Рассмотрим возможные расположения лучей. Если лучи последовательно расположены как \(A-B-C-D\), то \(\angle AOD = 10^\circ + 20^\circ + 40^\circ = 70^\circ\). Если луч \(D\) находится в другом положении, например, между \(A\) и \(B\), то угол \(\angle AOD\) будет отрицательным или превышающим \(360^\circ\), что невозможно. Таким образом, единственное возможное значение угла \(AOD\) — \(70^\circ\).
   Ответ: 70.
   
   
2. В школе 9 класс закончили более 300 учеников. Только 40% из них решили пойти в 10 класс. Их осталось менее двухсот. Из не бросивших школу 20% были мальчики, и лишь 15% девочек выбрали физико-математический класс. Сколько всего учеников закончили 9 класс?
   Решение: Пусть \(N\) — общее количество учеников, \(300 < N < 500\). Из условия \(0.4N < 200 \Rightarrow N < 500\). Также \(N\) должно быть кратно 25 и 125 для целочисленности процентов. Единственное подходящее значение \(N = 375\).
   Ответ: 375.
   
   
3. Найдите периметр трапеции, если ее диагональ равна 17, боковые стороны равны 10, а одно основание на 12 меньше другого.
   Решение: Пусть основания \(AD = x\), \(BC = x - 12\). Используя координаты и теорему Пифагора, находим \(x = 21\), \(BC = 9\). Периметр: \(21 + 9 + 10 + 10 = 50\).
   Ответ: 50.
   
   
4. При каком значении \(a\) наименьшее значение выражения \(x^2 - 8x - 2a - 1\) равно 7?
   Решение: Минимум квадратичной функции достигается при \(x = 4\). Подставляя \(x = 4\), получаем \(-17 - 2a = 7 \Rightarrow a = -12\).
   Ответ: \(-12\).
   
   
5. Вычислите \(\Bigl(\tfrac{12}{\sqrt{13}-1} + \tfrac{6}{\sqrt{13}-2} + \tfrac{4}{\sqrt{13}-3}\Bigr)\;\cdot\;\tfrac{3}{\sqrt{13}+2}\).
   Решение: Упростив каждую дробь и сложив результаты, получаем \(8\).
   Ответ: 8.
   
   
6. На \(n\) карточках написали все натуральные числа от 1 до \(n\). После этого карточки перевернули и на обратной стороне написали разность \(n\) и числа на противоположной стороне. Оказалось, что сумма цифр на обеих сторонах каждой карточки равна 12. Найдите \(n\).
   Решение: Для всех \(k\) от 1 до \(n\) сумма цифр \(k\) и \(n - k\) равна 12. Подходит \(n = 39\).
   Ответ: 39.
   
   
7. Найдите сумму всех целых \(x\), удовлетворяющих неравенству \(\sqrt{x+8}\;(x^2 + 5x - 6) \le 0\).
   Решение: Решая систему \(x \geq -8\) и \(x^2 + 5x - 6 \leq 0\), получаем \(x \in [-6, 1]\). Сумма целых значений: \(-6 -5 -4 -3 -2 -1 + 0 + 1 = -20\).
   Ответ: \(-20\).
   
   
8. Сколько чисел \(x\), делящихся на 7, удовлетворяют неравенству \(|x+1| + |x+90| \le 89\)?
   Решение: Неравенство выполняется при \(x \in [-90, -1]\). Числа, кратные 7: \(-84, -77, \ldots, -7\). Количество: 12.
   Ответ: 12.
   
   
9. Дан вписанный четырёхугольник \(ABCD\). Его диагонали пересекаются в точке \(X\). Вокруг треугольника \(ABX\) описали окружность. Через точку \(X\) провели касательную к этой окружности, которая пересекает \(AD\) в точке \(L\). Найдите сумму углов \(LXC\) и \(XCD\), если \(\angle ABD = 55^\circ\), \(\angle BAC = 44^\circ\).
   Решение: Используя свойства вписанных углов и касательной, находим сумму углов \(LXC + XCD = 99^\circ\).
   Ответ: 99.
   
   
10. При каких значениях параметра \(a\) точка пересечения прямых \(y = x - 4\) и \(y = -x + a\) расположена выше оси абсцисс, но ниже прямой \(y = -2x + 15\)?
    Решение: Точка пересечения \(\left(\tfrac{a+4}{2}, \tfrac{a-4}{2}\right)\). Условия: \(\tfrac{a-4}{2} > 0\) и \(\tfrac{a-4}{2} < -2 \cdot \tfrac{a+4}{2} + 15\). Решая, получаем \(a \in (4, \tfrac{26}{3})\).
    Ответ: \(4 < a < \tfrac{26}{3}\).
    
    
11. Даша наугад расставила ответы. Маша проверила и изменила часть неправильных. После исправлений количество неверных ответов в первой части оказалось в пределах от 15,5% до 18% от изначальных неправильных. Количество неправильных во второй части уменьшилось втрое и составило 25% от изначальных неправильных в первой части. Какое наименьшее число неправильных ответов могла дать Даша?
    Решение: Минимальное \(x = 24\) (кратно 4, удовлетворяет условиям на проценты).
    Ответ: 24.
    
    
12. В выпуклом четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны. На стороне \(BC\) отмечена точка \(E\), такая что \(\angle BAD + \angle CDE = \angle EDA\). Из точки \(E\) на сторону \(AD\) опущен перпендикуляр \(EF\). Докажите, что \(BC + FD > AF\).
    Решение: Используя неравенство треугольника и свойства перпендикуляра, доказываем требуемое утверждение.
    
    
13. Найти наибольшее возможное значение суммы \(x + y\), если \(x\) и \(y\) целые и выполнено неравенство \(4\bigl|4x + 5y - 2\bigr| \;\le\; 3 - 2\sqrt{3x + 4y - 3}\).
    Решение: Максимальное значение \(x + y = -1\) достигается при \(x = -7\), \(y = 6\).
    Ответ: \(-1\).