СУНЦ УРФУ им. Ельцина №10 (Урал) из 8 в 9 класс 2016 год вариант 1-2

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)

2016 год

Вариант 2

1. Решите уравнение: $\frac{5-|x+2|}{\sqrt{2-x}+1}=0$.
2. Упростите выражение и вычислите его при $x=\frac{1}{2}$ :
   $\begin{aligned} &\left(\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+1}\right) \cdot \sqrt{\left(x^{2}-2 x+1\right)} \\ \end{aligned}$
   
3. В городской Думе города $N$ меньше 50 депутатов. Девятая часть депутатов считает, что секвестр - мера полезная для экономики, третья - вредная, пятая - не знает значение этого слова, остальные - воздержались. Сколько было воздержавшихся?
4. Около окружности описана равнобедренная трапеция, средняя линия которой равна 5, а синус острого угла при основании равен $\frac{4}{5}$. Найдите площадь трапеции.
5. При каких значениях $m$ графики функции $y=3 x-5$ и $y=2 x+m$ пересекаются на оси ординат.
6. Решите неравенство: $\left(x^{2}+x-2\right)^{2}+\left(x^{2}-4\right)^{2} \leqslant 0$.
7. Вычислите: $\frac{3^{2 n-3} \cdot 7^{n-1}}{63^{n-1}}$ Ответ:
8. Постройте график функции $y=\frac{x-1}{1-x}+x$.
   
9. Четырехугольник $A B C D$ вписан в окружность. Угол $A B C$ равен $135^{\circ}$, угол $C A D$ равен $70^{\circ}$. Найдите градусную меру угла $A B D$. Ответ:
10. Решите неравенство: $\frac{\sqrt{18-7 x-x^{2}}}{x^{2}+2 x-15} \leqslant 0$.
    
    Часть С
    К заданиям приведите полное решение.
    С1. Решить уравнение: $\frac{2 x-7}{x^{2}-9 x+14}-\frac{1}{x^{2}-3 x+2}=\frac{1}{x-1}$.
    С2. Докажите, что число $345345 \ldots$ (группа цифр 345 повторяется 41 раз) делится на 15, но не делится на $45 .$
    С3. При каких значениях $q$ прямая $y=0,2 x+q$ образует с осями координат треугольник, площадь которого равна 40 кв.ед?
    С4. В остроугольном треугольнике $K L M$ проведены высоты $L E$ и $K H$.
    а) докажите, что треугольник $K L M$ подобен треугольнику $E H M$;
    б) найдите площадь треугольника $E H M$, если угол $L M K$ равен $45^{\circ}$, а площадь треугольника $K L M$ равна $10 \sqrt{2}$.
    

1. Ответы и решения к части B
   В1. Найдем область допустимых значений:
   $4-x \geqslant 0 ; x \leqslant 4 .$ Знаменатель $\sqrt{4-x}+2$ при всех $x$ из ОДЗ положителен. Приравняем к нулю числитель, получим
   $|x-3|-4=0 \Leftrightarrow|x-3|=4 \Leftrightarrow\left[\begin{array} { l } { x - 3 = 4 , } \\ { x - 3 = - 4 } \end{array} \Leftrightarrow \left[\begin{array}{l} x=7-\text { посторонний корень, } \\ x=-1-\text { подходит по ОДЗ. } \end{array}\right.\right.$
   $|x-3|-4=0 \Leftrightarrow|x-3|=4 \Leftrightarrow\left[\begin{array}{l}x-3=4, \\ x-3=-4\end{array} \Leftrightarrow\left[\begin{array}{l}x=7-\text { посторонний корень, } \\ x=-1-\text { подходит по ОДЗ. }\end{array}\right.\right.$ Ответ: $x=-1 .$
   В2. Найдем ОДЗ: $\left\{\begin{array}{l}x \geqslant 0, \\ \sqrt{x}-1 \neq 0\end{array} \Leftrightarrow\left\{\begin{array}{l}x \geqslant 0, \\ x \neq 1 .\end{array} \quad\right.\right.$ Приведем к общему знаменателю дроби.
   $\frac{(\sqrt{x}-1)(\sqrt{x}-1)+(\sqrt{x}+1)(\sqrt{x}+1)}{(\sqrt{x}+1)(\sqrt{x}-1)} \cdot \sqrt{(x-1)^{2}}=\frac{x-2 \sqrt{x}+1+x+2 \sqrt{x}+1}{x-1} \cdot \sqrt{(x-1)^{2}}=\frac{2 x+2}{x-1} \cdot|x-1| .$ Подставим $x=\frac{1}{2} .$ Получим
   $\frac{1+2}{-\frac{1}{2}} \cdot\left|-\frac{1}{2}\right|=\frac{3}{-\frac{1}{2}} \cdot \frac{1}{2}=-3$
   Ответ: $-3 .$
   В3. Пусть $x$ - количество учеников в классе. Так как нужно будет посчитать $\frac{1}{7}$ от $x, \frac{1}{3}$ от $x$ и $\frac{1}{2}$ от $x$, то $x$ должно делиться на 7, на 3 и на $2 .$ Такое подходящее число, меньшее пятидесяти - только $42 .$ Тогда $\frac{1}{7} \cdot 42=6-$ получили «5»,
   $\frac{1}{3} \cdot 42=14-$ получили $« 4$ »,
   $\frac{1}{2} \cdot 42=21-$ получили «3», $42-(6+14+21)=1-$ получили $« 2 » .$
   Ответ: $1 .$
   В4. Из треугольника $A B H$ имеем $h=A B \cdot \sin \angle A=5 \cdot \frac{3}{5}=3 .$ По свойству четырехугольника, описанного около окружности, получаем $a+b=A B+C D=5+5=10$, тогда $S=\frac{10}{2} \cdot 3=15$.
   Ответ: $15 .$
   В5. Графики пересекаются на оси абсцисс, следовательно $y=0 .$ Тогда $y=3 x+2=0 \Rightarrow x=-\frac{2}{3} \Rightarrow$ точка пересечения имеет координаты $\left(-\frac{2}{3} ; 0\right) .$ Подставим их во второе уравнение. Получим $0=2 \cdot\left(-\frac{2}{3}\right)+a \Rightarrow a=\frac{4}{3} .$ Ответ: $\frac{4}{3}$.
   В6. Так как $\left(x^{2}-x-2\right)^{2} \geqslant 0$ и $\left(x^{2}-1\right) \geqslant 0$, то левая часть или только положительна, или равна нулю. Последнее возможно лишь при $\left\{\begin{array}{l}x^{2}-x-2=0, \\ x^{2}-1=0\end{array} \Leftrightarrow\left\{\begin{array}{l}x=2 ; x=-1, \\ x=1 ; x=-1\end{array} \Leftrightarrow x=-1 .\right.\right.$
   Ответ: $x=-1 .$ B7. $\frac{7^{n+1} \cdot 2^{3 n-4}}{56^{n-1}}=\frac{7^{n+1} \cdot 2^{3 n-4}}{(7 \cdot 8)^{n-1}}=\frac{7^{n+1} \cdot 2^{3 n-4}}{7^{n-1} \cdot 8^{n-1}}=\frac{7^{n+1-(n-1)} \cdot 2^{3 n-4}}{2^{3 n-3}}=\frac{7^{2}}{2^{1}}=$ $\frac{49}{2}=24,5 .$
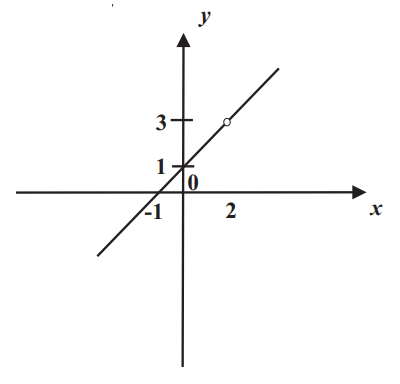
   B8. $y=x-\frac{x-2}{2-x}=x+1, x \neq 2$.
   
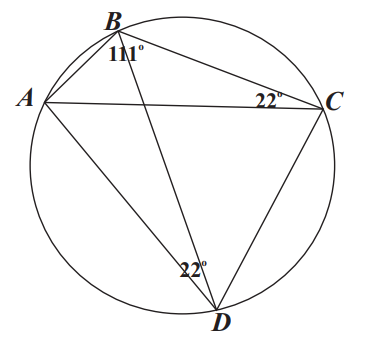
   В9. $\angle A C B=22^{\circ}=\angle A D B$, так как оба угла опираются на одну дугу $A B$, тогда $\angle B A C=180^{\circ}-11^{\circ}-22^{\circ}=47^{\circ}$.
   Ответ: $47^{\circ} .$
   
   В10. Найдем ОДЗ
   $\left\{\begin{array} { l } { - x ^ { 2 } - 1 0 x + 1 1 \geqslant 0 , } \\ { x ^ { 2 } + x - 1 2 \neq 0 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { x ^ { 2 } + 1 0 x - 1 1 \leqslant 0 , } \\ { x \neq - 4 , } \\ { x \neq 3 } \end{array} \Leftrightarrow \left\{\begin{array}{l} -11 \leqslant x \leqslant 1, \\ x \neq-4, x \neq 3 . \end{array}\right.\right.\right.$
   Числитель принимает только неотрицательные значения, значит знаменатель должен быть положительным, т.е. $x^{2}+x-12>0 .$ C учетом ОДЗ получаем $[-11 ;-4) \bigcup\{1\}$.
   Ответ: $[-11 ;-4) \bigcup\{1\} .$
   
   Решение и ответы к части С
   С1. $\frac{2 x+7}{(x+6)(x-1)}+\frac{3}{(x+3)(x+6)}=\frac{1}{x+3} .$ ОДЗ: $\left\{\begin{array}{l}x \neq-6, \\ x \neq 1, \\ x \neq-3\end{array} \quad\right.$ Приведем все дроби к общему знаменателю, получим: $(2 x+7)(x+3)+3(x-1)=(x+6)(x-1) \Leftrightarrow$ $2 x^{2}+7 x+6 x+21+3 x-3=x^{2}+6 x-x-6 \Leftrightarrow$ $x^{2}+11 x+24=0 .$ Из двух решений этого уравнения $x=-3-$ посторонний корень. Остается только $x=-8 .$
   Ответ: $x=-8$.
   С2. Число делится на 18, если оно делится на 2 и на 9. Число $234234 \ldots 234$ - четное число, значит делится на 2. А сумма цифр числа $-(2+3+4) \cdot 55=9 \cdot 55-$ делится на $9 .$ Чтобы число делилось на 36, необходимо, чтобы это число делилось на 9 и на $4 .$ На 9 мы уже проверку сделали. По признаку делимости на 4 необходимо, чтобы последние две цифры числа образовали число, которое делится на 4. Данное число оканчивается на 34, которое не делится на $4 .$
   С3. Так как линейная функция возрастает, то возможны два случая расположения прямой (при $p \geqslant 0$ и $p<0)$. Используя обозначения рисунка, имеем $S=$ $\frac{O A \cdot O B}{2}$, поЭтому
   $\begin{aligned} &S=\left|\frac{p(-p)}{2(0.3)}\right|=60 \Leftrightarrow p^{2}=0,6 \cdot 60 \Leftrightarrow p^{2}=36, \text { откуда } \\ &p=6 \text { или } p=-6 . \\ &\text { Ответ: } p=\pm 6 . \end{aligned}$
   
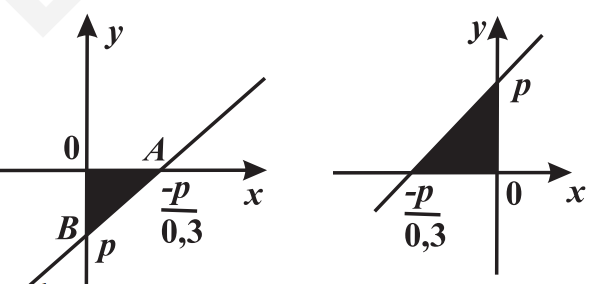
   C4. 1) $\triangle A F C \sim \triangle C H B$, по первому признаку $(\angle C-$ общий, оба прямоугольные треугольники). Запишем отношение пропорциональных сторон: $A C / C B=C F / C H .$ По свойству пропорции равенство можно записать так: $C H / C B=C F / A C$, но $C F / A C=\cos \angle C$.
   Рассмотрим треугольник $H C F$ и треугольник $A B C .$ Они подобны по двум пропорциональным сторонам и общему углу $C$, причем коэффициент подобия равен $k=\cos \angle C=\cos 30^{\circ}=\frac{\sqrt{3}}{2} .$ Отсюда $$ \begin{aligned} &\frac{S \triangle H F C}{S \triangle A B C}=k^{2}=\frac{3}{4}, \text { тогда } S_{\triangle H F C}=\frac{3}{4} \cdot 8 \sqrt{3}=6 \sqrt{3} . \\ &\text { Ответ: } 6 \sqrt{3} . \end{aligned} $$