СУНЦ УРФУ им. Ельцина №10 (Урал) из 8 в 9 класс 2015 год вариант 2-1
youit.school ©
СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)
2015 год
Вариант 2
Часть А
В заданиях A1–A10 записать ответ в указанном месте. Если получается несколько вариантов, нужно указать их все. Калькулятором, литературой, шпаргалкой и т.п. пользоваться нельзя
- Вычислите: $(8 \sqrt{12}+4 \sqrt{75}): 3 \sqrt{3}$. Ответ:
- Упростите выражение: $a(a-4)-(a-2)^{2}$. Ответ:
- Из формулы $y=\frac{a x}{3}$ выразите $x$. Ответ:
- В треугольнике $A B C$ угол $A=70^{\circ}$, угол $C=20^{\circ} .$ Найти угол между высотой $B H$ и биссектрисой $B D$. Ответ:
- Выполните деление дробей $\frac{6 x+6 y}{x}: \frac{x^{2}-y^{2}}{x^{2}} .$ Ответ:
- Решите систему уравнений: $\left\{\begin{array}{l}3 x-4 y=8, \\ 4 x+2 y=7 .\end{array}\right.$ Ответ:
- Решите неравенство: $3 x+1 \geqslant 2(x-1)+6 x$. Ответ:
- Не решая уравнение, определите сколько оно имеет корней. Соотнесите уравнение с ответами.
1) $2 x^{2}+3 x+5=0$.
2) $x^{2}-7 x+8=0$.
3) $4 x^{2}+4 x+1=0$.
А) Два корня.
Б) Один корень.
В) Нет действительных корней.
Ответ:
$\mathrm{A}$ $\mathrm{B}$ $\mathrm{B}$ - Расстояние между пристанями катер проходит по течению реки за 2 часа, а против течения реки за 3 часа. Какова скорость катера в стоячей воде, если скорость течения реки $5 \mathrm{Km} /$ ч?
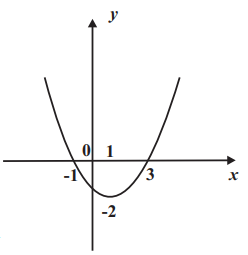
- По графику квадратичной функции найдите, при каких значениях $x$ значения функции отрицательны.
Решения и ответы к части А
1. Вычислите: $(8 \sqrt{12}+4 \sqrt{75}): 3 \sqrt{3}=(8 \sqrt{4 \cdot 3}+4 \cdot \sqrt{25 \cdot 3}): 3 \sqrt{3}=(16 \sqrt{3}+20 \sqrt{3}): 3 \sqrt{3}=36 \sqrt{3}:$ $3 \sqrt{3}=12$.
2. Упростите выражение: $a(a-4)-(a-2)^{2}=a^{2}-4 a-\left(a^{2}-4 a+4\right)=a^{2}-4 a-a^{2}+4 a-4=-4$.
3. Из формулы $y=\frac{a x}{3}$ выразите $x .$ Домножим уравнение на 3 , получим $3 y=a x ; x=\frac{3 y}{a}$.
4. $\angle B=180^{\circ}-70^{\circ}-20^{\circ}=90^{\circ} \Longrightarrow \triangle A B C-$ прямоугольный. $B D-$ биссектриса угла $B$, значит $\angle A B D=$ $45^{\circ}=\angle C B D .$ Тогда $\angle A B H=180^{\circ}-70^{\circ}-90^{\circ}=20^{\circ}$, тогда $\angle D B H=45^{\circ}-20^{\circ}=25^{\circ} .$
5. $\frac{6 x+6 y}{x}: \frac{x^{2}-y^{2}}{x^{2}}=\frac{6(x+y)}{x} \cdot \frac{x^{2}}{x^{2}-y^{2}}=\frac{6(x+y) \cdot x^{2}}{x \cdot(x-y)(x+y)}=\frac{6 x}{x-y}$.
6. $\left\{\begin{array}{l}3 x-4 y=8, \\ 4 x+2 y=7 .\end{array}\right.$ Домножим второе уравнение на 2, получим $\left\{\begin{array}{l}3 x-4 y=8, \\ 8 x+4 y=14 .\end{array} \quad\right.$ Сложим оба уравнения, получим $y=-\frac{1}{2}$.
Ответ: $\left(2 ;-\frac{1}{2}\right)$
7. $3 x+1 \geqslant 2(x-1)+6 x$ $3 x+1 \geqslant 2 x-2+6 x$ $3 x-2 x-6 x \geqslant-2-1$ $-5 x \geqslant-3$ $x \leqslant \frac{3}{5}$.
Ответ: $x \leqslant \frac{3}{5}$.
8. Найдем дискриминанты уравнений. Если $D0$, то уравнение имеет два различных корня.
1) $2 x^{2}+3 x+5=0 . \quad D=9-4 \cdot 2 \cdot 5<0 \quad-\quad$ нет корней.
2) $x^{2}-7 x+8=0 . \quad D=49-32>0 \quad-\quad$ два корня.
3) $4 x^{2}+4 x+1=0 . \quad D=16-16=0 \quad-\quad$ один корень.
$\mathrm{A}$ $\mathrm{B}$ $\mathrm{B}$ 2 3 1
9. Пусть $x$ км/ч - скорость катера в стоячей воде, тогда $x+5$ км/ч - скорость катера по течению, а $x-5 \mathrm{KM} / \mathrm{\varphi}$ - скорость катера против течения. По формуле $S=v \cdot t$ получаем $(x+5) \cdot 2=(x-5) \cdot 3$ $$ \begin{aligned} &2 x+10=3 x-15 \\ &x=25 \end{aligned} $$ 10. Функция имеет отрицательные значения при $x \in$ $(-1 ; 3)$. \\ \\ Часть В \\ Привести полное решение и ответ\\ В1. Найдите сумму корней уравнения: $16 x^{2}-4=0$.\\ В2. Найдите значение выражения $(4 x-1)^{2}-(4 x+1)^{2}$ при $x=\frac{1}{16}$.\\ В3. Цену на книгу снизили на $10 \%$, в результате чего она стоит теперь 45,9 рублей. Сколько стоила книга до снижения цены?\\ В4. В ромбе $A B C D$ диагональ $A C=4 \sqrt{13}$, а радиус вписанной окружности 6 . Найти площадь ромба.\\ В5. Известно, что график функции $y=a x^{2}-3 x+3$ проходит через точку $D(1 ; 2)$. Найдите абсциссу вершины параболы.\\ \\ Решения и ответы к части В\\ B1. $16 x^{2}-4=0$ $$ \begin{aligned} &16 x^{2}=4 \\ &x^{2}=\frac{1}{4} \\ &x_{1}=\frac{1}{2} \end{aligned} $$ $x_{2}=-\frac{1}{2}$ тогда сумма корней $\frac{1}{2}$ и $\left(-\frac{1}{2}\right)$ равна нулю. \\ Ответ: $0 .$ B2. $(4 x-1)^{2}-(4 x+1)^{2}=\left(16 x^{2}-8 x+1\right)-\left(16 x^{2}+8 x+1\right)=16 x^{2}-8 x+1-16 x^{2}-8 x-1=-16 x$. Тогда при $x=\frac{1}{16}$ получаем $-1$. \\ Ответ: $-1 .$ \\ В3. Пусть $x$ первоначальная цена книги, после снижения цены на $10 \%$, её стоимость составила $90 \%$ и стала равна 45,9 руб. Составим пропорцию: $\frac{x}{45,9}=\frac{100}{90} ; x=\frac{45,9 \cdot 100}{90}=51$ руб. \\ Ответ: 51 руб. \\ В4. $S_{\text {ромба }}=a \cdot h=B C \cdot 2 \cdot O H .$\\
\\
Радиус вписанной окружности составляет половину высоты ромба, значит высота равна $2 \cdot 6=12$. Осталось найти сторону ромба. Рассмотрим треугольник $B O C$ и треугольник $H O C .$ Они подобны по двум углам. Тогда $\frac{B C}{O C}=\frac{O C}{H C} ; \frac{B C}{2 \sqrt{13}}=\frac{2 \sqrt{13}}{4} ; B C=13 .$
$S_{A B C D}=B C \cdot h=13 \cdot 12=156 .$\\
Ответ: $156 .$
В5. Подставим координаты точки $D(1 ; 2)$ в уравнение $y=a x^{2}-$ $3 x+3$. Получим $2=a-3+3 ; a=2$. Тогда $y=2 x^{2}-3 x+3$. Найдем абсциссу вершины параболы по формуле $x_{0}=-\frac{b}{2 a} ; x_{0}=\frac{3}{4}$.\\
Ответ: $x=\frac{3}{4}$.
Материалы школы Юайти
youit.school ©
Решения задач
- Вычислите: $(8 \sqrt{12}+4 \sqrt{75}): 3 \sqrt{3}$.
Решение:
$8\sqrt{12} = 8 \cdot 2\sqrt{3} = 16\sqrt{3}$,
$4\sqrt{75} = 4 \cdot 5\sqrt{3} = 20\sqrt{3}$,
$(16\sqrt{3} + 20\sqrt{3}) : 3\sqrt{3} = 36\sqrt{3} : 3\sqrt{3} = 12$.
Ответ: 12.
- Упростите выражение: $a(a-4)-(a-2)^{2}$.
Решение:
$a(a-4) - (a^2 -4a +4) = a^2 -4a -a^2 +4a -4 = -4$.
Ответ: $-4$.
- Из формулы $y=\frac{a x}{3}$ выразите $x$.
Решение:
$y = \frac{a x}{3} \quad \Big| \cdot 3$,
$3y = a x \quad \Big| : a$,
$x = \frac{3y}{a}$.
Ответ: $x = \frac{3y}{a}$.
- В треугольнике $ABC$ угол $A=70^{\circ}$, угол $C=20^{\circ}$. Найти угол между высотой $BH$ и биссектрисой $BD$.
Решение:
$\angle B = 180^{\circ} -70^{\circ} -20^{\circ} =90^{\circ}$,
$\angle ABD = 45^{\circ}$ (биссектриса прямого угла),
$\angle ABH = 90^{\circ} -70^{\circ} =20^{\circ}$,
$\angle DBH =45^{\circ} -20^{\circ} =25^{\circ}$.
Ответ: $25^{\circ}$.
- Выполните деление дробей $\frac{6 x+6 y}{x}: \frac{x^{2}-y^{2}}{x^{2}}$.
Решение:
$\frac{6(x+y)}{x} \cdot \frac{x^2}{(x-y)(x+y)} = \frac{6x}{x-y}$.
Ответ: $\frac{6x}{x-y}$.
- Решите систему уравнений: $\left\{\begin{array}{l}3 x-4 y=8, \\ 4 x+2 y=7 .\end{array}\right.$
Решение:
Умножаем второе уравнение на 2:
$\left\{\begin{array}{l}3x -4y =8, \\ 8x +4y =14 \end{array}\right.$,
Складываем уравнения:
$11x =22 \Rightarrow x=2$,
Подставляем $x=2$ в первое уравнение:
$6 -4y =8 \Rightarrow y = -\frac{1}{2}$.
Ответ: $(2; -\frac{1}{2})$.
- Решите неравенство: $3 x+1 \geqslant 2(x-1)+6 x$.
Решение:
$3x +1 \geq 2x -2 +6x$,
$3x +1 \geq8x -2$,
$-5x \geq -3$,
$x \leq \frac{3}{5}$.
Ответ: $x \leq \frac{3}{5}$.
- Определите количество корней уравнений:
1) $2 x^{2}+3 x+5=0$,
2) $x^{2}-7 x+8=0$,
3) $4 x^{2}+4 x+1=0$.
Решение:
1) $D=9 -40 =-31 <0$ — нет корней (В),
2) $D=49 -32=17 >0$ — два корня (А),
3) $D=16 -16=0$ — один корень (Б).
Ответ:А Б В 2 3 1
- Скорость катера в стоячей воде.
Решение:
Пусть $x$ км/ч — скорость катера,
$(x+5) \cdot 2 = (x-5) \cdot 3$,
$2x +10 =3x -15$,
$x=25$.
Ответ: 25 км/ч.
- По графику квадратичной функции найдите, при каких значениях $x$ значения функции отрицательны.
Решение:
График пересекает ось $x$ в точках $-1$ и $3$, ветви направлены вверх.
Ответ: $x \in (-1; 3)$.
- Найдите сумму корней уравнения: $16 x^{2}-4=0$.
Решение:
$16x^2 =4$,
$x^2 =\frac{1}{4}$,
$x_1 =\frac{1}{2}$, $x_2 =-\frac{1}{2}$,
Сумма корней: $\frac{1}{2} + (-\frac{1}{2}) =0$.
Ответ: 0.
- Найдите значение выражения $(4 x-1)^{2}-(4 x+1)^{2}$ при $x=\frac{1}{16}$.
Решение:
$(4x-1)^2 - (4x+1)^2 = (16x^2 -8x +1) - (16x^2 +8x +1) =-16x$,
При $x=\frac{1}{16}$: $-16 \cdot \frac{1}{16} =-1$.
Ответ: $-1$.
- Найдите первоначальную цену книги.
Решение:
Пусть $x$ руб. — первоначальная цена,
$0,9x =45,9$,
$x =\frac{45,9}{0,9} =51$.
Ответ: 51 руб.
- Найдите площадь ромба.
Решение:
Высота ромба $h=2 \cdot 6=12$,
Сторона ромба $BC=13$,
Площадь: $13 \cdot 12=156$.
Ответ: 156.
- Найдите абсциссу вершины параболы.
Решение:
Подставляем точку $D(1;2)$ в уравнение:
$2 =a -3 +3 \Rightarrow a=2$,
Абсцисса вершины: $x_0 = \frac{3}{4}$.
Ответ: $\frac{3}{4}$.
Материалы школы Юайти