8 800 707 6729
8 800 707 6729Telegram канал

СУНЦ УРФУ им. Ельцина №10 (Урал) из 8 в 9 класс 2015 год вариант 1-2

Сложность:
Дата экзамена: 2015
Печать
youit.school ©

СУНЦ УРФУ ИМ. ЕЛЬЦИНА №10 (УРАЛ)


2015 год


Вариант 2



Часть В
К заданиям части В приведите только ответ, записав его в отведенном месте. Переписывать решение задачи в чистовик не нужно.

  1. Упростите выражение: $\frac{x^{2}}{x+2} \sqrt{1+\frac{4(1+x)}{x^{2}}}$, если $-2<x<0 .$
  2. Решите уравнение: $\left|x^{2}-8 x+7\right|=\left|x^{2}+x+1\right|$.
  3. В остроугольном треугольнике $A B C$ известно, что $\angle A=$ $60^{\circ}, B C=4 \sqrt{3}$. Найдите радиус окружности, описанной около этого треугольника.
  4. Решите неравенство: $(x+3)\left(x^{2}-5 x+4\right)<(x+3)^{2}(x+6)$.
  5. На день рождения Карлсону подарили мешок с конфетами: шоколадными и карамельками. Всего конфет в мешке было меньше 100 , причем соотношение шоколадных и карамелек было $9: 7$. Карлсон сразу же съел $25 \%$ всех конфет, причем $20 \%$ из них составляли карамельки. Сколько шоколадных конфет осталось в мешке?
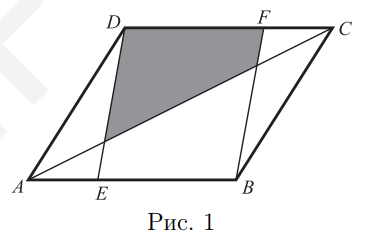
  6. Площадь параллелограмма $A B C D$ равна 6. На сторонах $A B$ и $C D$ отмечены точки $E$ и $F$ (рис. 1), так что $A E: E B=C F: F D=$ $=1: 2 .$ Найдите площадь заштрихованной части.
  7. Какова последняя цифра числа $17^{2015}+17 ?$
  8. Упростите выражение: $\frac{3}{\sqrt{3+2 \sqrt{2}}-\sqrt{2}} .$
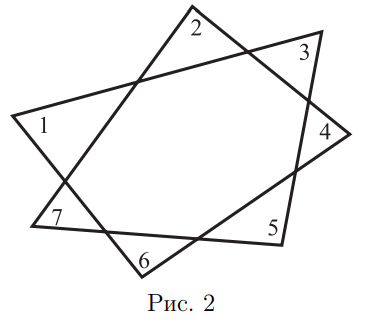
  9. Какова сумма углов, отмеченных на рис. $2 ?$
  10. Постройте график функции $y=\frac{x-1}{|x-1|} x$ (ответ изобразите на координатной системе ниже).
    Ответы на часть В
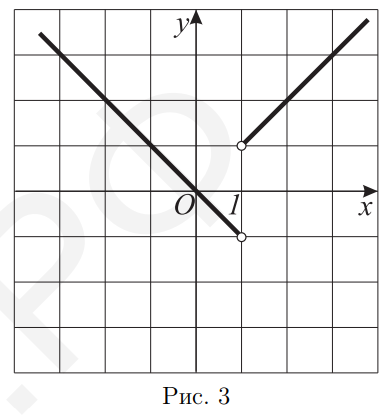
    B1.-x; B2. $\frac{2}{3} ; \quad$ B3. $4 ; \quad$ B4. $x \in(-\infty ;-3) \cup(-1 ;+\infty) ; \quad$ B5. $29 ; \quad$ B6. $2 ; \quad$ B7. $0 ; \quad$ B8. $3 ;$ В9. $540^{\circ} ; \quad$ В10. См. рис. 3.


    Часть С
    К заданиям части С нужно привести в чистовике полное решение и ответ.
  11. Решите уравнение: $\frac{x^{2}-2 x}{3-x}+1=\frac{3}{3-x}$.
  12. На военном параде движется колонна солдат длиной 500 м со скоростью 5 км/ч. Из конца колонны в ее начало с донесением отправляется связной со скоростью 7 км/ч. Передав донесение командиру, он с той же скоростью возвращается назад в конец колонны. Какое расстояние пробежит связной?
    1. Докажите, что прямая, проходящая через середину меньшего основания трапеции и точку пересечения ее диагоналей, проходит через середину большего основания.
    2. Найдите длину отрезка, соединяющего середины оснований трапеции, если ее диагонали перпендикулярны, а длины оснований равны 2 и $5 .$
  14. Найдите сумму квадратов корней уравнения $x^{2}+(2+a) x-2+3 a=0$ и установите, при каких значениях а она будет наименьшей.
    Ответы на задания части С
    C1.0; C2. $\frac{49}{24}$ км; С3. 3,$5 ;$ С4. $(a-1)^{2}+7$, наименьшее значение при $a=1 .$
Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростите выражение: $\frac{x^{2}}{x+2} \sqrt{1+\frac{4(1+x)}{x^{2}}}$, если $-2<x<0 .$
    Решение: \[ 1 + \frac{4(1 + x)}{x^{2}} = \frac{(x + 2)^2}{x^{2}} \] \[ \sqrt{\frac{(x + 2)^2}{x^{2}}} = \frac{|x + 2|}{|x|} = \frac{x + 2}{-x} \quad (\text{т.к. } x < 0) \] \[ \frac{x^{2}}{x + 2} \cdot \frac{x + 2}{-x} = -x \] Ответ: $-x$.
  2. Решите уравнение: $\left|x^{2}-8 x+7\right|=\left|x^{2}+x+1\right|$.
    Решение: \[ x^{2} - 8x + 7 = x^{2} + x + 1 \quad \Rightarrow \quad -9x + 6 = 0 \quad \Rightarrow \quad x = \frac{2}{3} \] \[ x^{2} - 8x + 7 = -x^{2} - x - 1 \quad \Rightarrow \quad 2x^{2} -7x +8 = 0 \quad (\text{нет корней}) \] Ответ: $\frac{2}{3}$.
  3. В остроугольном треугольнике $A B C$ известно, что $\angle A=60^{\circ}, B C=4 \sqrt{3}$. Найдите радиус окружности, описанной около этого треугольника.
    Решение: \[ R = \frac{BC}{2\sin A} = \frac{4\sqrt{3}}{2 \cdot \frac{\sqrt{3}}{2}} = 4 \] Ответ: $4$.
  4. Решите неравенство: $(x+3)\left(x^{2}-5 x+4\right)<(x+3)^{2}(x+6)$.
    Решение: \[ (x + 3)(x^2 -5x +4 - (x +3)(x +6)) < 0 \] \[ x^2 -5x +4 -x^2 -9x -18 = -14x -14 \] \[ (x +3)(-14(x +1)) 0 \] Ответ: $x \in (-\infty; -3) \cup (-1; +\infty)$.
  5. Карлсон съел $25\%$ конфет, из них $20\%$ — карамельки. Изначальное соотношение шоколадных и карамелек $9:7$. Общее число конфет кратно $16$ и меньше $100$. Подходит $N=80$: \[ \text{Шоколадных осталось: } \frac{9}{16} \cdot 80 - 0,2 \cdot 80 = 45 - 16 = 29 \] Ответ: $29$.
  6. Площадь заштрихованной части параллелограмма равна $2$.
    Ответ: $2$.
  7. Последняя цифра числа $17^{2015} + 17$: \[ 17^{2015} \mod 10 = 3, \quad 17 \mod 10 = 7 \quad \Rightarrow \quad 3 + 7 = 10 \quad \Rightarrow \quad 0 \] Ответ: $0$.
  8. Упростите выражение: $\frac{3}{\sqrt{3+2 \sqrt{2}}-\sqrt{2}}$.
    Решение: \[ \sqrt{3 + 2\sqrt{2}} = \sqrt{2} + 1 \] \[ \frac{3}{(\sqrt{2} +1) - \sqrt{2}} = 3 \] Ответ: $3$.
  9. Сумма углов пятиугольника: $540^{\circ}$.
    Ответ: $540^{\circ}$.
  10. График функции $y = \frac{x-1}{|x-1|} x$ состоит из двух лучей: $y = x$ при $x > 1$ и $y = -x$ при $x < 1$.
    Ответ: см. рис. 3.
  11. Решите уравнение: $\frac{x^{2}-2 x}{3-x}+1=\frac{3}{3-x}$.
    Решение: \[ x^2 -2x +3 -x =3 \quad \Rightarrow \quad x^2 -3x =0 \quad \Rightarrow \quad x =0 \] Ответ: $0$.
  12. Связной пробежит: \[ \text{Время до начала: } \frac{0,5}{2} =0,25 \text{ ч}, \quad \text{Обратно: } \frac{0,5}{12} = \frac{1}{24} \text{ ч} \] \[ \text{Общее расстояние: } 7 \cdot 0,25 +7 \cdot \frac{1}{24} = \frac{49}{24} \text{ км} \] Ответ: $\frac{49}{24}$ км.
    1. Прямая через середину меньшего основания и точку пересечения диагоналей делит большее основание пополам (свойство трапеции).
    2. Длина отрезка между серединами оснований: \[ \frac{2 +5}{2} =3,5 \] Ответ: $3,5$.
  14. Сумма квадратов корней уравнения: \[ x_1^2 +x_2^2 = (x_1 +x_2)^2 -2x_1x_2 = (a -1)^2 +7 \] Минимум при $a=1$.
    Ответ: $(a-1)^2 +7$, наименьшее значение при $a=1$.
Материалы школы Юайти