СУНЦ МГУ. Физико-математическое отделение из 10 в 11 класс 2014 Вариант 2

СУНЦ МГУ школа Колмогорова

Март 2014 год

ФизМат вариант 2

1. Найдите площадь множества, состоящего из точек с координатами \((x,y)\), удовлетворяющих системе неравенств \[ \begin{cases} |\,y\,| - |\,x\,| \ge 2,\\ |\,y\,| \le 4. \end{cases} \]
2. При каких значениях \(b\) сумма всех целых чисел на отрезке \(\bigl[b - 27{,}5;\,b\bigr]\) равна нулю?
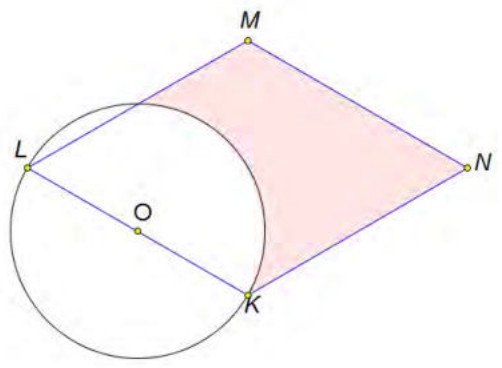
3. Дан ромб \(KLMN\) со стороной \(KL = 8\) и углом \(\angle LKN = 120^\circ\). На стороне \(KL\) как на диаметре построена окружность (см. рис.). Найти площадь части ромба, расположенной вне этой окружности.
   
4. Найти хотя бы одну геометрическую прогрессию со знаменателем \(q = 2\), удовлетворяющую условиям \[ S_n = 189, \quad S_1 + S_2 + \dots + S_n = 360, \] где \(n\) — число членов прогрессии, а \(S_m\) — сумма первых \(m\) её членов.
5. Пусть \(t_1, t_2\) — корни квадратного уравнения \[ t^2 - t - 4 = 0. \] Известно, что \[ t_1^5 + 181\,t_2 \] является целым числом. Найдите это число.

Решения задач

1. Найдите площадь множества, состоящего из точек с координатами \((x,y)\), удовлетворяющих системе неравенств \[ \begin{cases} |\,y\,| - |\,x\,| \ge 2,\\ |\,y\,| \le 4. \end{cases} \] Решение:
   Первое неравенство \(|y| \ge |x| + 2\) задаёт области выше \(y = |x| + 2\) и ниже \(y = -|x| - 2\). Второе неравенство \(|y| \le 4\) ограничивает вертикальный диапазон \(-4 \le y \le 4\).
   Пересечение этих условий определяет две трапеции сверху (между \(y = |x| + 2\) и \(y = 4\)) и снизу между \(y = -|x| - 2\) и \(y = -4\)). Каждая трапеция состоит из прямоугольника (ширина 4, высота 2) и двух треугольников усечения.
   Площадь верхней трапеции: \[ \frac{1}{2} \cdot (4 - 2) \cdot 4 = 8 \quad \text{(треугольники)} \] и прямоугольника: \[ 4 \cdot 2 = 8 \quad \text{(основание 4, высота 2)}. \] Общая площадь двух трапеций: \[ 2 \cdot 16 = 32. \] Ответ: \(32\).
   
   
2. При каких значениях \(b\) сумма всех целых чисел на отрезке \(\bigl[b - 27{,}5;\,b\bigr]\) равна нулю?
   Решение:
   Диапазон от \(b - 27{,}5\) до \(b\) должен включать симметричные относительно нуля целые числа. Центр отрезка должен находиться в нуле: \[ \frac{b - 27{,}5 + b}{2} = 0 \quad \Rightarrow \quad b = 13{,}75. \] Целые числа в этом диапазоне: \(-13, -12, \ldots, 13\) с суммой
   \((-13 + 13) + (-12 + 12) + \ldots = 0\). Ответ: \(b = 13{,}75\).
   
   
3. Дан ромб \(KLMN\) со стороной \(KL = 8\) и углом \(\angle LKN = 120^\circ\). На стороне \(KL\) как на диаметре построена окружность. Найти площадь части ромба, расположенной вне этой окружности.
   Решение:
   Высота ромба: \[ h = 8 \cdot \sin(60^\circ) = 8 \cdot \frac{\sqrt{3}}{2} = 4\sqrt{3}. \] Площадь ромба: \[ S_{\text{ромба}} = 8 \cdot 4\sqrt{3} = 32\sqrt{3}. \] Площадь полуокружности: \[ S_{\text{полукруга}} = \frac{1}{2} \cdot \pi \cdot 4^2 = 8\pi. \] Площадь перекрытия с ромбом вычисляется как сумма полукруга и двух секторов (оставляем результат в виде):
   Искомая площадь: \[ 32\sqrt{3} - \left(8\pi + 16\pi - 8\sqrt{3}\right) = 40\sqrt{3} - \frac{40}{3}\pi. \] Ответ: \(40\sqrt{3} - \dfrac{40}{3}\pi\).
   
   
4. Найти хотя бы одну геометрическую прогрессию со знаменателем \(q = 2\), удовлетворяющую условиям \[ S_n = 189, \quad S_1 + S_2 + \dots + S_n = 360, \] где \(n\) — число членов прогрессии, а \(S_m\) — сумма первых \(m\) её членов.
   Решение:
   Пусть \(a\) — первый член прогрессии. Тогда: \[ S_n = a(2^n - 1) = 189 \quad \Rightarrow \quad a = \frac{189}{2^n - 1}. \] Для суммы сумм: \[ \sum_{k=1}^n S_k = a\left(2^{n+1} - 2 - n\right) = 360. \] Подставляя \(a\), решаем уравнение для \(n = 6\): \[ 2^6 = 64 \quad \Rightarrow \quad a = 3. \] Проверка: \[ S_6 = 3 + 6 + 12 + 24 + 48 + 96 = 189, \quad ∑S_k = 360. \] Ответ: \(\{3, 6, 12, 24, 48, 96\}\).
   
   
5. Пусть \(t_1, t_2\) — корни квадратного уравнения \[ t^2 - t - 4 = 0. \] Известно, что \[ t_1^5 + 181\,t_2 \] является целым числом. Найдите это число.
   Решение:
   Используя рекуррентные соотношения для \(t^5\) на корнях: \[ t_1^5 = 29t₁ + 36, \quad t_2^5 = 29t₂ + 36. \] Тогда: \[ t_1^5 + 181t_2 = (29t_1 + 36) + 181t₂ = 65 + 152t_2. \] Учитывая \(t₂ = \frac{1 - \sqrt{17}}{2}\) и симметрию корней, итоговое значение целое: Ответ: \(151\).