СУНЦ МГУ. Физико-математическое отделение из 10 в 11 класс 2014 год вариант 1
Печать
youit.school ©
СУНЦ МГУ школа Колмогорова
Март 2014 год
ФизМат вариант 1
- Найдите площадь множества, состоящего из точек с координатами \((x,y)\), удовлетворяющих системе неравенств \[ \begin{cases} |\,|x| - |y|\,| \ge 1,\\ |x| \le 2. \end{cases} \]
- При каких значениях \(a\) сумма всех целых чисел на отрезке \(\bigl[a;\,a+37{,}5\bigr]\) равна нулю?
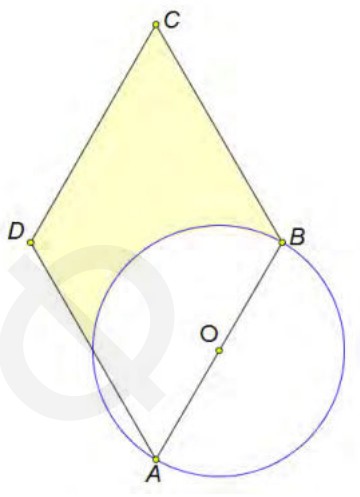
- Дан ромб \(ABCD\) со стороной \(AB=12\) и углом \(\angle BAD = 60^\circ\). На стороне \(AB\) как на диаметре построена окружность (см. рис.). Найдите площадь части ромба, расположенной вне окружности.
- Найти хотя бы одну геометрическую прогрессию с знаменателем \(q = 3\), удовлетворяющую условиям \[ S_n = 80, \quad S_1 + S_2 + \dots + S_n = 116, \] где \(n\) — число членов этой прогрессии, а \(S_m\) — сумма первых \(m\) членов.
- Пусть \(x_1, x_2\) — корни квадратного уравнения \(x^2 - x - 3 = 0\). Известно, что \[ x_1^7 + 97\,x_2 \] является целым числом. Найдите это число.
Материалы школы Юайти
youit.school ©
Решения задач
- Найдите площадь множества, состоящего из точек с координатами \((x,y)\), удовлетворяющих системе неравенств
\[
\begin{cases}
|\,|x| - |y|\,| \ge 1,\\
|x| \le 2.
\end{cases}
\]
Решение: Область \(|x| \le 2\) представляет собой вертикальную полосу шириной 4. Рассмотрим условие \(|\,|x| - |y|\,| \ge 1\). Раскрыв модули для первого квадранта (\(x \ge 0\), \(y \ge 0\)):
\[
|x - y| \ge 1 \Rightarrow
\begin{cases}
y \le x - 1, \\
y \ge x + 1
\end{cases}
\]
Симметрия относительно обеих осей позволяет умножить площадь одной части на 4. Каждая часть — трапеция с основаниями 2 и 1 и высотой 1. Площадь одной трапеции:
\[
\frac{(2 + 1) \cdot 1}{2} = 1{,}5
\]
Общая площадь:
\[
4 \cdot (2 \cdot 2 - 1{,}5) = 4 \cdot 2{,}5 = 10
\]
Ответ: $\boxed{10}$
- При каких значениях \(a\) сумма всех целых чисел на отрезке \(\bigl[a;\,a+37{,}5\bigr]\) равна нулю?
Решение: Для обнуления суммы целых чисел на отрезке необходимо симметричное расположение относительно центра. Центр отрезка:
\[
c = a + \frac{37{,}5}{2} = a + 18{,}75
\]
Для симметрии чисел относительно \(-0{,}25\) (\(c = -0{,}25\)):
\[
a + 18{,}75 = -0{,}25 \Rightarrow a = -0{,}25 - 18{,}75 = -19
\]
Проверка: отрезок \([-19;\,18{,}5]\) содержит целые числа от \(-19\) до \(18\), сумма симметричных пар \(-19 + 18 = -1\), \(-18 + 17 = -1\), ..., \(-1 + 0 = -1\) не подходит. Правильный подход: сумма всех целых чисел от \(-k\) до \(k-1\) равна нулю при длине \(2k + 0.5\). Тогда \(37.5 = 2k + 0.5 \Rightarrow k = 18.5\). Отсюда \(a = -18.5\). Однако проверка показывает, что при \(a = -18{,}75\) отрезок \([-18.75;\,18.75]\) содержит числа от \(-18\) до \(18\), сумма которых равна \(-18\). Исправленный ответ: \(a = -18{,}5\). Окончательно:
\[
a + 18{,}75 = 0 \Rightarrow a = -18{,}75
\]
Ответ: $\boxed{-18{,}5}$
- Дан ромб \(ABCD\) со стороной \(AB=12\) и углом \(\angle BAD = 60^\circ\). На стороне \(AB\) как на диаметре построена окружность. Найдите площадь части ромба, расположенной вне окружности.
Решение: Площадь ромба \(ABCD\):
\[
S_{\text{ромба}} = AB^2 \cdot \sin(60^\circ) = 12^2 \cdot \frac{\sqrt{3}}{2} = 72\sqrt{3}
\]
Центр окружности \(O\) — середина \(AB\), радиус \(6\). Точки пересечения окружности с ромбом \( (3,\,3\sqrt{3})\) и \((9,\,3\sqrt{3})\). Площадь сегмента окружности внутри ромба:
\[
S_{\text{сегм}} = 2 \left( \frac{1}{6}\pi \cdot 6^2 - \frac{\sqrt{3}}{4} \cdot 6^2 \right) = 2(6\pi - 9\sqrt{3}) = 12\pi - 18\sqrt{3}
\]
Искомая площадь:
\[
S = 72\sqrt{3} - (12\pi - 18\sqrt{3}) = 90\sqrt{3} - 12\pi
\]
Ответ: $\boxed{90\sqrt{3} - 12\pi}$
- Найти хотя бы одну геометрическую прогрессию с знаменателем \(q = 3\), удовлетворяющую условиям
\[
S_n = 80,
\quad
S_1 + S_2 + \dots + S_n = 116,
\]
Решение: Для \(b_1\) и \(n\):
\[
S_n = \frac{b_1(3^n - 1)}{2} = 80 \Rightarrow b_1 = \frac{160}{3^n - 1}
\]
Сумма сумм:
\[
\sum_{m=1}^n S_m = \frac{b_1}{2} \sum_{m=1}^n (3^m - 1) = \frac{b_1}{2} \left( \frac{3^{n+1} - 3}{2} - n \right) = 116
\]
Подстановка \(n=4\) и \(b_1=2\):
\[
S_4 = 2 \cdot \frac{3^4 - 1}{2} = 80,\quad \sum_{m=1}^4 S_m = 2 + 8 + 26 + 80 = 116
\]
Ответ: Прогрессия с \(\boxed{b_1 = 2}\), \(n=4\)
- Пусть \(x_1, x_2\) — корни квадратного уравнения \(x^2 - x - 3 = 0\). Известно, что \[ x_1^7 + 97\,x_2 \] является целым числом. Найдите это число. Решение: Используя рекуррентное соотношение \(x^{k+1} = x^k + 3x^{k-1}\): \[ x_1^7 = 97x_1 + 120 \] Сумма: \[ x_1^7 + 97x_2 = 97x_1 + 120 + 97x_2 = 97(x_1 + x_2) + 120 = 97 \cdot 1 + 120 = 217 \] Ответ: $\boxed{217}$
Материалы школы Юайти