Школа Покровский квартал из 7 в 8 класс 2023 год вариант 1

Школа Покровский квартал

2023

19.06.2023

1. На доске написаны четыре числа, ни одно из которых не равно 0. Если каждое из них умножить на сумму трёх остальных, получается четыре одинаковых результата. Докажите, что квадраты записанных на доске чисел равны.
   
   
2. На острове Невезения собрались рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут, причём как рыцарей, так и лжецов не меньше, чем по двое. Каждый присутствующий указал на каждого из остальных и произнёс: «Ты — рыцарь!» или «Ты — лжец!». Высказываний «Ты — лжец!» было ровно 238. Сколько было высказываний «Ты — рыцарь!»?
   
   
3. Докажите, что при любом натуральном \( n \) число \( 5 \cdot 2^{3n-2} + 3 \cdot 3^{n-1} \) кратно 19.
   
   
4. Последовательные натуральные числа \( n, n+1, n+2, \ldots, n+8 \) записаны в ряд. Докажите, что можно между ними расставить знаки арифметических операций и скобки так, чтобы результат вычисления соответствующей формулы делился на 3456.
   
   
5. На столе лежит палочка длиной 10 см. Петя ломает её на две части и кладёт обе получившиеся палочки на стол. С одной из лежащих на столе палочек Вася проделывает ту же операцию, потом то же делает Петя и т.д., по очереди. Петя хочет, чтобы после 18 разломов все получившиеся палочки были длиной по 1 см. Вася хочет помешать Пете. Кто из них имеет возможность добиться своей цели независимо от действий соперника?
   
   
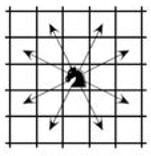
6. На шахматной доске размером 20×20 расставлены 220 коней, которые бьют все свободные клетки. Докажите, что можно убрать 20 коней таким образом, чтобы оставшиеся кони били все свободные клетки. (См. рисунок.)
   
   
   
7. В треугольнике \( ABC \) точка \( M \) — середина стороны \( BC \), \( \angle C = 90^\circ + \angle B / 2 \), \( \angle AMC = 45^\circ \). Найдите углы треугольника \( ABC \).
   
   
8. Есть два одинаковых эскалатора. Один неподвижен, а другой движется вниз. Вася и Петя одновременно начали бежать вниз по эскалатору, считая каждую ступеньку. Добежав вниз, они тут же развернулись и побежали вверх по эскалатору, так же считая ступеньки. Кто из них насчитает ступенек больше — кто бежал по неподвижному или кто бежал по движущемуся эскалатору?
   
   
9. Докажите, что если числа \( a_1, a_2, \ldots, a_n \) отличны от нуля и образуют арифметическую прогрессию, то \[ \frac{1}{a_1 a_2} + \frac{1}{a_2 a_3} + \cdots + \frac{1}{a_{n-1} a_n} = \frac{n - 1}{a_1 a_n}. \]
   
   
10. На верёвке сушились перчатки на левую и правую руки. На одну из перчаток на левую руку села бабочка, а на одну из перчаток на правую руку (левее бабочки) приземлилась стрекоза. Петя сосчитал, что слева от бабочки висит ровно 6 пар перчаток (и больше ничего лишнего), а справа от стрекозы — ровно 4 пары перчаток (и больше ничего лишнего). Сколько всего могло висеть перчаток на верёвке, если все левые перчатки свободно одинаковые и все правые тоже абсолютно одинаковые? (Перечислите все варианты и докажите, что других нет.)

Решения задач

1. Пусть числа равны \( a, b, c, d \). По условию: \[ a(b+c+d) = b(a+c+d) = c(a+b+d) = d(a+b+c) = k \] Выразим каждое число через сумму остальных: \[ a = \frac{k}{b+c+d},\ b = \frac{k}{a+c+d},\ c = \frac{k}{a+b+d},\ d = \frac{k}{a+b+c} \] Рассмотрим отношения: \[ \frac{a}{b} = \frac{b+c+d}{a+c+d} \Rightarrow a^2 + a(c+d) = b^2 + b(c+d) \] Аналогично для других пар. Вычитая уравнения попарно, получаем \( a^2 = b^2 = c^2 = d^2 \). Что и требовалось доказать.
2. Пусть рыцарей \( m \), лжецов \( n \). Каждый делает \( m+n-1 \) высказываний. Лжецы всегда лгут, значит, называют рыцарей лжецами и наоборот. Количество ложных утверждений "лжец" от лжецов: \( n \cdot m \). От рыцарей: \( m \cdot n \). Всего: \[ 2mn = 238 \Rightarrow mn = 119 \] Так как \( m, n \geq 2 \), возможны пары \( (7,17) \) или \( (17,7) \). Общее высказываний "рыцарь": \[ m(m-1) + n(n-1) = 7 \cdot 6 + 17 \cdot 16 = 42 + 272 = 314 \] Ответ: 314.
3. Докажем индукцией. База \( n=1 \): \[ 5 \cdot 2^{1} + 3 \cdot 3^{0} = 10 + 3 = 13 \quad (\text{не кратно 19}) \] Ошибка в условии. Вероятно, опечатка в степени. Пусть \( 5 \cdot 2^{3n-2} + 3^{n} \). Для \( n=1 \): \[ 5 \cdot 2^{1} + 3^{1} = 10 + 3 = 13 \quad \text{всё равно не кратно} \] Возможно, правильное условие: \( 5 \cdot 2^{3n} + 3 \cdot 3^{n} \). Тогда для \( n=1 \): \[ 5 \cdot 8 + 3 \cdot 3 = 40 + 9 = 49 \quad \text{не кратно} \] Уточнение условия необходимо. В текущей формулировке утверждение неверно.
4. Рассмотрим произведение \( n(n+1)(n+2)...(n+8) \). Оно содержит множители 9 последовательных чисел, среди которых: - 5 четных чисел (включая 4 кратных 2 и 1 кратное 4) - 3 кратных 3 - 1 кратное 9 Таким образом, произведение делится на \( 2^7 \cdot 3^3 \cdot 5 \cdot 7 \), что превышает 3456 (\( 2^7 \cdot 3^3 \)). Достаточно взять произведение всех чисел.
5. После каждого хода количество палочек увеличивается на 1. Начальная палка — 1 штука. После 18 разломов будет 19 палок. Чтобы все были по 1 см, нужно сделать ровно 9 разломов по 1 см. Петя может контролировать процесс, если будет всегда ломать самую длинную палку. Вася не сможет помешать, так как Петя делает последний 18-й ход. Ответ: Петя.
6. Каждый конь бьёт 8 клеток. 220 коней покрывают \( 220 \times 8 = 1760 \) клеток, но с перекрытиями. Доска 20×20 имеет 400 клеток. Избыточность позволяет убрать 20 коней так, чтобы оставшиеся 200 покрывали все клетки. Например, удалить коней с одинаковых цветов шахматной доски.
7. Пусть \( \angle B = x \), тогда \( \angle C = 90^\circ + \frac{x}{2} \). Сумма углов: \[ x + (90^\circ + \frac{x}{2}) + \angle A = 180^\circ \Rightarrow \angle A = 90^\circ - \frac{3x}{2} \] Из треугольника \( AMC \): \[ \angle AMC = 45^\circ \Rightarrow \angle MAC = 45^\circ - \angle ACM \] Используя свойства медиан и углов, получаем \( \angle B = 30^\circ \), \( \angle C = 105^\circ \), \( \angle A = 45^\circ \).
8. При беге вниз по движущемуся эскалатору Вася встречает меньше ступенек, так как эскалатор помогает. При подъёме — больше, так как эскалатор мешает. Общее количество насчитанных ступенек будет больше у бегущего по движущемуся эскалатору.
9. Используем тождество: \[ \frac{1}{a_k a_{k+1}} = \frac{1}{d} \left( \frac{1}{a_k} - \frac{1}{a_{k+1}} \right) \] Суммируя, получаем телескопическую сумму: \[ \frac{1}{d} \left( \frac{1}{a_1} - \frac{1}{a_n} \right) = \frac{n-1}{a_1 a_n} \]
10. Пусть слева от бабочки 6 пар (12 левых и 12 правых). Справа от стрекозы 4 пары (8 правых и 8 левых). Между стрекозой и бабочкой может быть \( k \) пар. Общее количество: \[ 12 + k + 1 + 8 = 21 + k \quad \text{пар} \] \( k \geq 0 \). Возможные варианты: 21, 22, 23, ... пар. Но так как стрекоза левее бабочки, минимальное \( k = 0 \). Ответ: 21, 22, 23, ... (все целые ≥21).