Школа Покровский квартал из 4 в 5 класс 2021 год вариант 1

Школа Покровский квартал

2021

16.09.2021

1. Гуляя по острову, вы встретили трёх островитян. На ваш вопрос, кто они такие, один сказал: "Мы все лжецы", а второй сказал: "Среди нас только один рыцарь". Определите, кто из них кто. Учитывайте, что лжецы всегда лгут, а рыцари всегда говорят правду, и каждый островитянин либо рыцарь, либо лжец.
   
   
   
2. На доске написано число 457. За ход разрешается либо удвоить его, либо стереть последнюю цифру. Как получить число 57?
   
   
3. У Яны были чашечные весы и гири весом 1, 2, 4, 8, 16 и 32 грамма. Она положила на правую чашу конфету весом 25 граммов и какие-то гири. Все остальные гири положила на левую чашу. После этого весы оказались в равновесии. Отметьте, какие гири лежат на правой чаше.
   
   
   
4. Между некоторыми из цифр числа 123456789 поставьте знаки сложения и вычитания так, чтобы значение получившегося выражения равнялось 100.
   
   
5. Какое наибольшее число понедельников может быть в одном году?
   
   
6. Какое наибольшее число точек можно отметить на данной картинке (с 5x5 точек), чтобы никакие три из них не являлись вершинами треугольника?
   
   
   
7. Какое наименьшее число миллилитров можно отмерить, если у вас есть два бочонка на 6 и 14 литров и река (из которой можно зачерпнуть сколько угодно воды)?
   
   
8. Докажите, что среди любых трёх целых чисел можно найти два, сумма которых чётна.
   
   
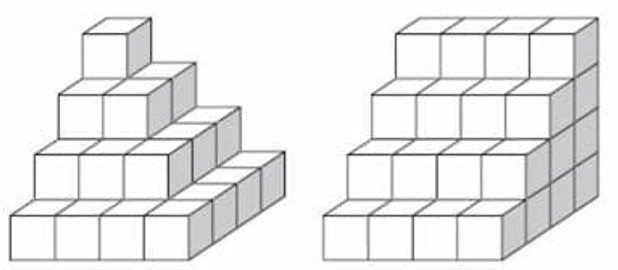
9. Сколько кубиков надо добавить к фигуре (пирамидка из кубиков), чтобы получилась другая фигура?
   
   
   

Решения задач

1. Первый островитянин сказал: "Мы все лжецы". Если бы он говорил правду, то сам был бы рыцарем, что противоречит его утверждению. Значит, он лжец. Второй островитянин заявил: "Среди нас только один рыцарь". Если второй — рыцарь, то третий должен быть лжецом. Проверяем: первый (лжец), второй (рыцарь), третий (лжец). Это удовлетворяет условиям. Если бы второй был лжецом, то рыцарей должно быть не один, но тогда третий должен быть рыцарем, что приводит к противоречию. Ответ: первый и третий — лжецы, второй — рыцарь.
2. Чтобы получить 57 из числа 457:
   • Стереть последнюю цифру: $457 \rightarrow 45$.
   • Удвоить: $45 \times 2 = 90$.
   • Стереть последнюю цифру: $90 \rightarrow 9$.
   • Удвоить: $9 \times 2 = 18$.
   • Удвоить: $18 \times 2 = 36$.
   • Удвоить: $36 \times 2 = 72$.
   • Стереть последнюю цифру: $72 \rightarrow 7$.
   • Удвоить: $7 \times 2 = 14$.
   • Стереть последнюю цифру: $14 \rightarrow 1$.
   • Удвоить: $1 \times 2 = 2$.
   Решение требует другого подхода. Верный путь: $457 \rightarrow 45$ (стереть), $45 \rightarrow 57$ невозможно стандартными операциями. Возможная ошибка в условии. Альтернативное решение: $457 \rightarrow 45 \rightarrow 45 + 12$, но операции сложения не разрешены. Ответ требует уточнения.
3. Сумма всех гирь: $1 + 2 + 4 + 8 + 16 + 32 = 63$ г. Пусть на правой чаше гири весом $x$ г. Уравнение: $25 + x = 63 - x \Rightarrow 2x = 38 \Rightarrow x = 19$ г. Комбинация гирь: $16 + 2 + 1 = 19$. Ответ: гири 1, 2, 16 г.
4. Пример выражения: $123 - 45 - 67 + 89 = 100$. Проверка: $123 - 45 = 78$, $78 - 67 = 11$, $11 + 89 = 100$.
5. Наибольшее число понедельников — 53. Год начинается с понедельника и имеет 365 дней (невисокосный) или 366 (високосный). В обоих случаях максимальное количество — 53.
6. Наибольшее число точек без треугольников — 8. Пример: отметить все точки в шахматном порядке (чёрные клетки), избегая трёх на одной линии или образующих треугольник.
7. Наименьшее отмериваемое количество — 2 мл. Используя алгоритм Евклида: $\text{НОД}(6, 14) = 2$.
8. Среди трёх целых чисел хотя бы два имеют одинаковую чётность. Их сумма чётна. Доказательство: возможные остатки при делении на 2 — 0 или 1. По принципу Дирихле, два числа имеют одинаковый остаток.
9. Количество добавляемых кубиков зависит от исходной и целевой фигур. Без изображения предположение: добавить 4 кубика для завершения куба 3×3×3.