Школа №777 из 7 в 8 класс 2021 год вариант 1

1. Разложите на множители многочлен (3 балла):
   1. (а) \((a - 12)^3 - 125\)
   2. (б) \(16 - (x^2 + 2xy + y^2)\)
   3. (в) \(m^5 - 8m^3n + 16mn^2\)
   
   
   
2. Решите уравнения (3 балла):
   1. (а) \(c^3 + 4c^2 = 0\)
   2. (б) \(6\Bigl(\tfrac{2}{3}x - 1\Bigr) +(-2x - 3) = 2(x - 3)\)
   3. (в) \(\lvert 2x + 3\rvert = 5\)
   
   
   
3. (2 балла) Задайте линейную функцию формулой, график которой параллелен прямой \[ -4x - y + 2 = 0 \] и проходит через точку \(N(1;4)\). Постройте её график.
   
   
4. (3 балла) Упростите выражение: \[ \frac{7^{2n+1}\,\cdot\,22^{2x-1}\,\cdot\,2^{1-n}} {14^n\;\cdot\;77^{n-3}\;\cdot\;11^{\,n+2}}. \]
   
   
5. Решите задачу с пояснениями (2 балла):
   От пристани \(A\) вниз по течению реки отошла лодка собственной скоростью \(12\)км/ч, а через \(1\)ч из \(A\) вверх по течению отправился катер собственной скоростью \(18\)км/ч. Найдите скорость течения реки, если через \(3\)ч после выхода лодки расстояние между лодкой и катером составляло \(75\)км.
   
   
6. Решите задачу с пояснениями (4 балла):
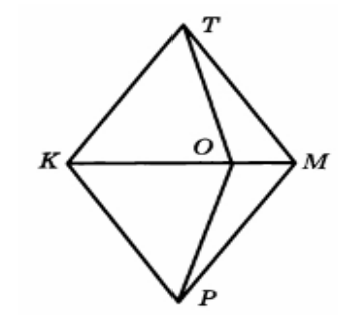
   На рисунке \(KT = TM = MP = PK\).
   
   
   1. Докажите, что \(KT \parallel PM\) и \(TM \parallel KP\).
   2. Докажите, что \(TO = OP\).
   3. Докажите, что точка \(O\) равноудалена от прямых \(TM\) и \(PM\).
   
   
   
   
   
   
7. Решите задачу с пояснениями (3 балла):
   Четыре одинаковые рубашки дешевле куртки на 16%. На сколько процентов пять таких же рубашек дороже куртки?
   
   
8. (3 балла) Приведите пример шестизначного натурального числа, которое записывается только цифрами 1 и 2 и делится на 72. В ответе укажите ровно одно такое число и приведите подробное решение.
   
   

Решения задач

1. Разложите на множители многочлен:
   1. (а) \((a - 12)^3 - 125\)
      Решение: Используем формулу разности кубов:
      \((a - 12)^3 - 5^3 = (a - 12 - 5)((a - 12)^2 + 5(a - 12) + 25)\)
      Упростим:
      \((a - 17)(a^2 - 24a + 144 + 5a - 60 + 25) = (a - 17)(a^2 - 19a + 109)\)
      Ответ: \((a - 17)(a^2 - 19a + 109)\).
      
      
   2. (б) \(16 - (x^2 + 2xy + y^2)\)
      Решение: Выделяем квадрат суммы:
      \(16 - (x + y)^2 = 4^2 - (x + y)^2 = (4 - x - y)(4 + x + y)\)
      Ответ: \((4 - x - y)(4 + x + y)\).
      
      
   3. (в) \(m^5 - 8m^3n + 16mn^2\)
      Решение: Выносим общий множитель \(m\):
      \(m(m^4 - 8m^2n + 16n^2) = m(m^2 - 4n)^2\)
      Ответ: \(m(m^2 - 4n)^2\).
   
   
   
2. Решите уравнения:
   1. (а) \(c^3 + 4c^2 = 0\)
      Решение: Выносим \(c^2\) за скобки:
      \(c^2(c + 4) = 0 \Rightarrow c = 0\) (кратность 2), \(c = -4\)
      Ответ: \(c = 0\), \(c = -4\).
      
      
   2. (б) \(6\left(\dfrac{2}{3}x - 1\right) + (-2x - 3) = 2(x - 3)\)
      Решение:
      \(4x - 6 - 2x - 3 = 2x - 6\)
      \(2x - 9 = 2x - 6 \Rightarrow -9 = -6\) – нет решений.
      Ответ: Нет корней.
      
      
   3. (в) \(|2x + 3| = 5\)
      Решение: Рассмотрим два случая:
      \(2x + 3 = 5 \Rightarrow x = 1\)
      \(2x + 3 = -5 \Rightarrow x = -4\)
      Ответ: \(x = 1\), \(x = -4\).
   
   
   
3. Задайте линейную функцию, график которой параллелен прямой \(-4x - y + 2 = 0\) и проходит через \(N(1; 4)\).
   Решение: Преобразуем уравнение прямой \(y = -4x + 2\). Угловой коэффициент \(k = -4\).
   Подставляем точку \(N\) в уравнение \(y = -4x + b\):
   \(4 = -4 \cdot 1 + b \Rightarrow b = 8\)
   Ответ: \(y = -4x + 8\).
   
   
4. Упростите выражение: \[ \dfrac{7^{2n+1} \cdot 22^{2x-1} \cdot 2^{1-n}}{14^n \cdot 77^{n-3} \cdot 11^{n+2}} \]
   Решение: Раскладываем основания на простые множители:
   Числитель: \(7^{2n+1} \cdot (2 \cdot 11)^{2x-1} \cdot 2^{1-n} = 7^{2n+1} \cdot 2^{2x-n} \cdot 11^{2x-1}\)
   Знаменатель: \(2^n \cdot 7^{2n-3} \cdot 11^{2n-1}\)
   Упрощаем степени:
   \(7^{4} \cdot 2^{2x-2n} \cdot 11^{2x-2n} = 7^{4} \cdot (22)^{2x-2n}\)
   Ответ: \(2401 \cdot (22)^{2x-2n}\).
   
   
5. Найдите скорость течения реки:
   Решение: Пусть скорость течения \(v\) км/ч. Лодка прошла \(3(12 + v)\). Катер прошел \(2(18 - v)\). Уравнение:
   \(3(12 + v) + 2(18 - v) = 75\)
   \(36 + 3v + 36 - 2v = 75 \Rightarrow v = 3\)
   Ответ: 3 км/ч.
   
   
6. Докажите утверждения:
   1. KTMP – ромб (все стороны равны). В ромбе противоположные стороны параллельны: \(KT \parallel PM\), \(TM \parallel KP\).
   2. Диагонали ромба делятся пополам: \(TO = OP\).
   3. Точка \(O\) – центр ромба, равноудалена от всех сторон, поэтому она равноудалена от прямых \(TM\) и \(PM\).
   
   
   
7. На сколько процентов пять рубашек дороже куртки:
   Решение: Пусть \(C\) – стоимость куртки. Четыре рубашки: \(0.84C\). Одна рубашка: \(0.21C\). Пять рубашек: \(1.05C\). На 5% дороже.
   Ответ: на 5%.
   
   
8. Пример шестизначного числа из цифр 1 и 2, делящегося на 72:
   Решение: Число должно делиться на 8 и 9. Сумма цифр: 9 (три единицы и три двойки). Последние три цифры: 112 (делится на 8). Пример: 122112. Проверка: \(122112 ÷ 72 = 1696\).
   Ответ: 122112.