Школа №777 из 7 в 8 класс 2021 год вариант 1

1. Разложите на множители многочлен (3 балла):
   1. (а) \((m + 3)^3 - 8\)
   2. (б) \((a^2 + 2ab + b^2) - c^2\)
   3. (в) \(4a^3b + 8a^2b^2 + ab^3\)
   
   
   
2. Решите уравнения (3 балла):
   1. (а) \(x^2 - 3x = 0\)
   2. (б) \(4\bigl(2x - \tfrac{1}{4}\bigr) - (x + 1) = 7\bigl(x + \tfrac{2}{7}\bigr)\)
   3. (в) \(\lvert x - 1\rvert = 3\)
   
   
   
3. (2 балла) Задайте линейную функцию формулой, график которой параллелен прямой \[ 2x - y + 4 = 0 \] и проходит через точку \(N(0; -2)\). Постройте её график.
   
   
4. (3 балла) Упростите выражение: \[ \frac{ 15^n \cdot 39^{\,n+1} \cdot 3^{\,2-n} \cdot 5^n }{ 3^{\,n-1} \cdot 65^{\,2n-2} \cdot 13^{\,3-n} }. \]
   
   
5. (2 балла) Решите задачу с пояснениями:
   От пристани \(A\) отошёл плот. Одновременно с ним от пристани \(B\) вверх по течению реки по направлению к \(A\) отошла моторная лодка. Лодка и плот встретились через \(2\) ч, а расстояние между пристанями \(A\) и \(B\) равно \(16\) км. Найдите собственную скорость лодки.
   
   
6. (4 балла) Решите задачу с пояснениями:
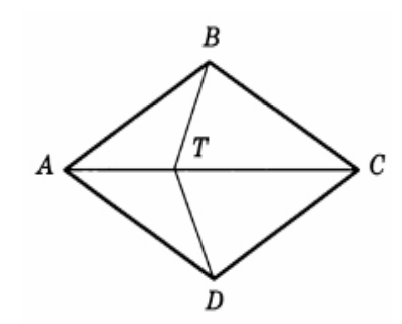
   На рисунке \(AB = BC = CD = DA\).
   
   
   1. Докажите, что \(AB \parallel CD\) и \(BC \parallel AD\).
   2. Докажите, что \(BT = DT\).
   3. Докажите, что точка \(T\) равноудалена от прямых \(AB\) и \(AD\).
   
   
   
   
   
   
7. (3 балла) Решите задачу с пояснениями:
   В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате их цена стала на \(9\%\) ниже, чем при открытии торгов в понедельник. На сколько процентов подорожали акции в понедельник?
   
   
8. (3 балла) Найдите шестизначное натуральное число, которое записывается только цифрами \(1\) и \(0\) и делится на \(24\). Приведите подробное решение.
   
   

Решения задач

1. Разложите на множители многочлен:
   1. (а) \((m + 3)^3 - 8\)
      Решение: Представим выражение как разность кубов:
      \((m + 3)^3 - 2^3 = (m + 3 - 2)\left((m + 3)^2 + (m + 3) \cdot 2 + 2^2\right)\)
      \(= (m + 1)(m^2 + 8m + 19)\)
      Ответ: \((m + 1)(m^2 + 8m + 19)\)
      
      
   2. (б) \((a^2 + 2ab + b^2) - c^2\)
      Решение: Группируем первые три слагаемых и применяем формулу разности квадратов:
      \((a + b)^2 - c^2 = (a + b - c)(a + b + c)\)
      Ответ: \((a + b - c)(a + b + c)\)
      
      
   3. (в) \(4a^3b + 8a^2b^2 + ab^3\)
      Решение: Вынесем общий множитель \(ab\):
      \(ab(4a^2 + 8ab + b^2)\)
      Ответ: \(ab(4a^2 + 8ab + b^2)\)
   
   
   
2. Решите уравнения:
   1. (а) \(x^2 - 3x = 0\)
      Решение: Вынесем \(x\) за скобки:
      \(x(x - 3) = 0 \Rightarrow x = 0\) или \(x = 3\)
      Ответ: \(0; 3\)
      
      
   2. (б) \(4\left(2x - \frac{1}{4}\right) - (x + 1) = 7\left(x + \frac{2}{7}\right)\)
      Решение: Раскроем скобки и упростим:
      \(8x - 1 - x - 1 = 7x + 2 \Rightarrow 7x - 2 = 7x + 2 \Rightarrow -2 = 2\) — уравнение не имеет решений.
      Ответ: Нет решения
      
      
   3. (в)\(|x - 1| = 3\)
      Решение: Рассмотрим два случая:
      \(x - 1 = 3 \Rightarrow x = 4\)
      \(x - 1 = -3 \Rightarrow x = -2\)
      Ответ: \(-2; 4\)
   
   
   
3. Задайте линейную функцию, параллельную прямой \(2x - y + 4 = 0\) и проходящую через \(N(0; -2)\)
   Решение: Приведем уравнение исходной прямой к виду \(y = 2x + 4\). У параллельной прямой \(k = 2\). Подставляем координаты точки:
   \(-2 = 2 \cdot 0 + b \Rightarrow b = -2\). Уравнение: \(y = 2x - 2\)
   Ответ: \(y = 2x - 2\). График — прямая через точки \((0; -2)\) и \((1; 0)\)
   
   
4. Упростите выражение: \[ \frac{15^n \cdot 39^{n+1} \cdot 3^{2-n} \cdot 5^n}{3^{n-1} \cdot 65^{2n-2} \cdot 13^{3-n}} \]
   Решение: Переведем числа в простые множители:
   Числитель: \( (3 \cdot 5)^n \cdot (3 \cdot 13)^{n+1} \cdot 3^{2-n} \cdot 5^n = 3^{n+3} \cdot 5^{2n} \cdot 13^{n+1}\)
   Знаменатель: \(3^{n-1} \cdot (5 \cdot 13)^{2n-2} \cdot 13^{3-n} = 3^{n-1} \cdot 5^{2n-2} \cdot 13^{n+1}\)
   Сокращение множителей: \( \frac{3^4 \cdot 5^2}{1} = 81 \cdot 25 = 2025\)
   Ответ: \(2025\)
   
   
5. Решите задачу с пояснениями: Плот и лодка встретились через 2 часа. Собственная скорость лодки
   Решение: Пусть скорость течения \(x\) км/ч, собственная скорость лодки \(v\) км/ч. Составляем уравнение на расстояние:
   \(2(v - x) + 2x = 16 \Rightarrow 2v = 16 \Rightarrow v = 8\) км/ч
   Ответ: \(8\) км/ч
   
   
6. Геометрическая задача:
   1. (а) \(AB \parallel CD\) и \(BC \parallel AD\) по свойству сторон ромба
   2. (б) Точка пересечения диагоналей делит их пополам ⇒ \(BT = DT\)
   3. (в) Точка \(T\) лежит на диагонали-биссектрисе угла ⇒ равноудаленность от сторон
   
   
   
7. Решите задачу с изменением цены акций:
   Решение: Прирост и спад на \(x\%\): \((1 + x)(1 - x) = 0.91\). Решаем уравнение:
   \(1 - x^2 = 0.91 \Rightarrow x^2 = 0.09 \Rightarrow x = 0.3\) ⇒ \(30\%\)
   Ответ: \(30\%\)
   
   
8. Найдите 6-значное число из 0 и 1, делящееся на 24
   Решение: Последние 3 цифры должны быть \(000\) (делимость на 8), сумма цифр делится на 3. Пример: \(111000\)
   Проверка: \(111000 ÷ 24 = 4625\). Ответ: \(111000\)