Школа №777 из 4 в 5 класс 2021 вариант 2

1. Решить уравнение (2 балла): \[ (7\cdot x + 14)\colon4 \;-\; 8 \;=\; 6. \]
   
   
2. Выполните задание с пояснениями (2 балла):
   На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 10 кусков; по жёлтым — 8 кусков; по зелёным — 8 кусков. Сколько кусков получится, если распилить палку по всем линиям трёх цветов?
   
   
3. Решите задачу с пояснениями (3 балла):
   Грузовой поезд проехал 420 км, сделав остановку на одной станции. Путь до этой станции занял 4 ч при скорости 80 км/ч. Остаток пути поезд преодолел за 2 ч. С какой скоростью он двигался после остановки?
   
   
4. Выполните задание (3 балла, дополнительно 1 балл за рациональные вычисления значения выражения):
   Найдите число, 30% которого равно значению выражения \[ 412\cdot468\colon39 \;+\; 702\colon39\cdot412 \;+\; 84\cdot2\cdot96\cdot5. \]
   
   
5. Выполните задание с пояснениями (3 балла):
   Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 12, 18 и 30. Найдите площадь четвёртого прямоугольника.
   
   

1. Выполните задание с пояснениями (1 балл):
   Определите закономерность и найдите пропущенное число:
   
   
   
   
   
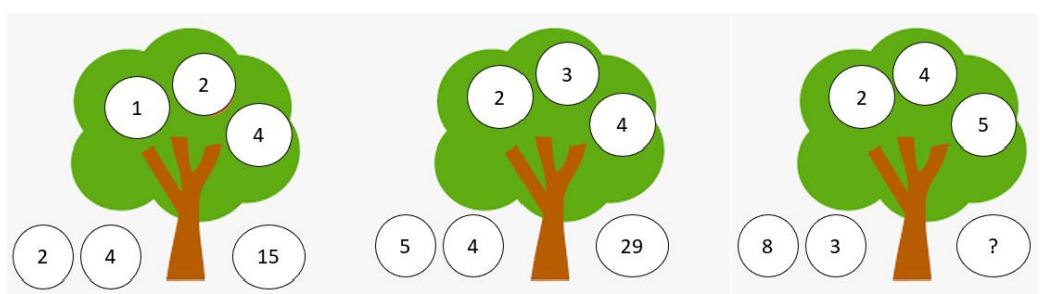
2. Выполните задание с пояснениями (2 балла):
   Губке Бобу срочно нужно налить из водопроводного крана 6 л воды. Но он имеет лишь два сосуда: 5‑литровый и 7‑литровый. Как ему это сделать?
   
   
3. Выполните задание с пояснениями (3 балла):
   На одной чашке весов лежат 6 апельсинов, а на другой – 2 дыни. Если добавить одну такую же дыню к апельсинам, весы уравновесятся. Сколько апельсинов весит одна дыня?

Решения задач

1. Решить уравнение: $(7\cdot x + 14)\colon4 \;-\; 8 \;=\; 6$
   Решение:
   $(7x + 14) : 4 - 8 = 6$
   $(7x + 14) : 4 = 6 + 8 = 14$
   $7x + 14 = 14 \cdot 4 = 56$
   $7x = 56 - 14 = 42$
   $x = 42 : 7 = 6$
   Ответ: 6.
2. Сколько кусков получится, если распилить палку по всем линиям трёх цветов?
   Решение: Количество красных линий: $10 - 1 = 9$. Жёлтых и зелёных линий по $8 - 1 = 7$ каждая. Всего линий: $9 + 7 + 7 = 23$. Тогда число кусков: $23 + 1 = 24$.
   Ответ: 24.
3. С какой скоростью двигался поезд после остановки?
   Решение:
   Путь до остановки: $80 \text{ км/ч} \cdot 4 \text{ ч} = 320 \text{ км}$.
   Остаток пути: $420 - 320 = 100 \text{ км}$.
   Скорость после остановки: $\frac{100 \text{ км}}{2 \text{ ч}} = 50 \text{ км/ч}$.
   Ответ: 50 км/ч.
4. Найдите число, 30% которого равно значению выражения \[ 412\cdot468\colon39 \;+\; 702\colon39\cdot412 \;+\; 84\cdot2\cdot96\cdot5 \] Решение:
   Первое слагаемое: $412 \cdot (468 : 39) = 412 \cdot 12 = 4944$.
   Второе слагаемое: $(702 : 39) \cdot 412 = 18 \cdot 412 = 7416$.
   Третье слагаемое: $84 \cdot 2 \cdot 96 \cdot 5 = 84 \cdot 10 \cdot 96 = 840 \cdot 96 = 80640$.
   Сумма: $4944 + 7416 + 80640 = 93000$.
   Искомое число: $93000 : 0,3 = 310000$.
   Ответ: 310000.
5. Найдите площадь четвёртого прямоугольника.
   Решение:
   Пусть левый верхний прямоугольник 12, правый верхний 18, правый нижний 30. Обозначим стороны: ширина левой части $a$, правой $c$, высота верхней $b$, нижней $d$.
   Из соотношений: $ab = 12$, $cb = 18$, $cd = 30$. Четвёртая площадь $ad = \frac{ab \cdot cd}{cb} = \frac{12 \cdot 30}{18} = 20$.
   Ответ: 20.
6. Найти пропущенное число:
   Решение: В первом ряду: $9 \cdot 2 = 18$, $18 \cdot 2 = 36$. Во втором ряду аналогично: $8 \cdot 2 = 16$, $16 \cdot 2 = 32$.
   Ответ: 32.
7. Получить 6 л воды сосудами 5 и 7 л:
   Решение:
   1. Наполнить 7 л, перелить в 5. В 7 л осталось 2 л.
   2. Вылить 5 л, перелить 2 л из 7 л в 5 л.
   3. Наполнить 7 л.
   4. Долить в 5 л до заполнения (3 л), в 7 л останется $7 - 3 = 4$ л.
   5. Вылить 5 л, перелить 4 л из 7 л в 5 л.
   6. Наполнить 7 л, долить 1 л в 5 л. В 7 л останется 6 л.
   Ответ: последовательность действий позволяет получить 6 л в 7-литровом сосуде.
8. Сколько апельсинов весит одна дыня?
   Решение:
   Пусть веса: $6a = 2d$, где $a$ — апельсин, $d$ — дыня. После добавления: $6a + d = 3d$ (весы уравновешены). Из $6a = 2d$ получаем $d = 3a$.
   Ответ: 3.