Школа №777 из 4 в 5 класс 2020 вариант 1

1. Вычислите:
   1. (а) (1 балл) К произведению чисел $300602$ и $405$ прибавить разность чисел $400030$ и $280417$.
   2. (б) (1 балл) $38\text{ м }76\text{ см}+58\text{ см}-4\text{ м }2\text{ дм }9\text{ см}$.
   3. (в) (2 балла) $785400:385:5+(4237\cdot16-3237\cdot16)-6409+1$.
   
   
   
2. Решите уравнения:
   1. (а) (1 балл) $4487+1049:x=5536$.
   2. (б) (2 балла) $43+(x-46:25):75=193$.
   
   
   
3. Решите задачу с пояснениями (2 балла):
   В 9:00 из города A в город B выехал один автомобиль со скоростью 54 км/ч. Другой автомобиль в 10:00 выехал из города A, в 13:00 он обогнал первый автомобиль и в 19:00 прибыл в город B. В котором часу прибыл в город B первый автомобиль?
   
   
4. Решите задачу с пояснениями (3 балла):
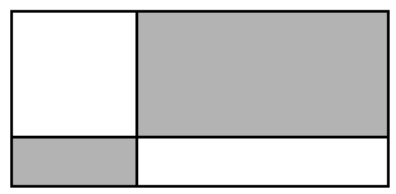
   Прямоугольный лист бумаги разделили на четыре части, одна из которых — квадрат. Периметры серых прямоугольников равны 32 см и 18 см. Найдите периметр и площадь листа бумаги.
   
   
   
   
   
5. Решите задачу с пояснениями (3 балла):
   Двум работникам фабрики игрушек поручили слепить из глины 48 петушков и 40 курочек. Оля делает петушка за 5 минут, а курочку — за 3 минуты. Света тратит на любую игрушку по 4 минуты. Придумайте, как мастерам распределить работу, чтобы, работая вдвоём, закончить её как можно скорее. Найдите, сколько времени потребует ваш способ.
   
   
6. Решите задачу с пояснениями (3 балла):
   В семье три сестры. Известно, что Маша родилась на следующий год после того года, когда до рождения младшей из сестёр оставалось 5 лет, а Таня родилась на два года раньше, чем средней исполнилось 3 года. Сейчас Оле 10 лет. Сколько лет Тане и Маше?
   
   
7. Задача (3 балла):
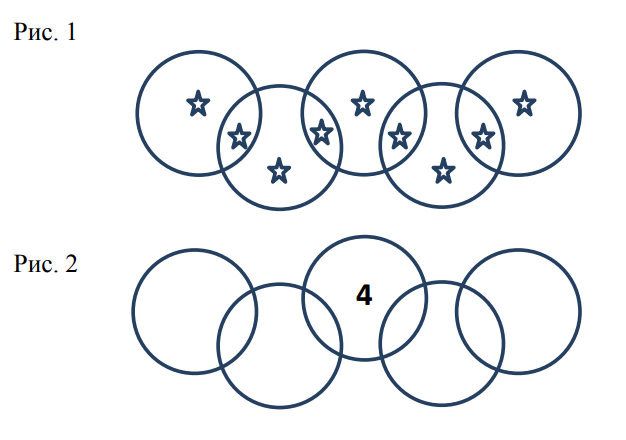
   Мальвина велела Буратино вместо звёздочек (см. рис. 1) написать различные цифры от 1 до 9 так, чтобы сумма цифр в каждом круге равнялась 14. Одну цифру (см. рис. 2) Буратино написал. Помогите расставить остальные.
   
   
   
   
   

Решения задач

1. Выполните действия:
   1. (а) (1 балл) К произведению чисел $300602$ и $405$ прибавить разность чисел $400030$ и $280417$.
      Решение: \begin{align} 300602 \cdot 405 &= (3 \cdot 10^5 + 602) \cdot 405 \\ &= 121,743,810 + 243,810 = 121,987,620. \\ 400,030 - 280,417 &= 119,613. \\ 121,987,620 + 119,613 &= 122,107,233. \end{align} Ответ: 122 107 233.
   2. (б)(1 балл) $38\text{ м }76\text{ см}+58\text{ см}-4\text{ м }2\text{ дм }9\text{ см}$.
      Решение: \begin{align} 38\:м\:76\:см &= 3876\:см \\ 3876\:см + 58\:см &= 3934\:см \\ 4\:м\:2\:дм\:9\:см &= 400 + 20 + 9 = 429\:см \\ 3934\:см - 429\:см &= 3505\:см = 35\:м\:5\:см. \end{align} Ответ: 35 м 5 см.
   3. (в) (2 балла) $785400:385:5+(4237\cdot16-3237\cdot16)-6409+1$.
      Решение: \begin{align} 785400 \div 385 \div 5 &= \frac{785400}{385 \cdot 5} = \frac{785400}{1925} = 408. \\ 4237 \cdot 16 - 3237 \cdot 16 &= 16 \cdot (4237 - 3237) = 16 \cdot 1000 = 16000. \\ 408 + 16000 - 6409 + 1 &= 16000 - 6409 + 409 = 16000 - 5999 = 10001. \end{align} Ответ: 10 001.
2. Решите уравнения:
   1. (а) (1 балл) $4487 + \frac{1049}{x} = 5536$.
      Решение: \begin{align} \frac{1049}{x} &= 5536 - 4487 = 1049 \\ x &= \frac{1049}{1049} = 1. \end{align} Ответ: 1.
   2. (б) (2 балла) $43 + \frac{x - \frac{46}{25}}{75} = 193$.
      Решение: \begin{align} \frac{x - 1.84}{75} &= 193 - 43 = 150 \\ x - 1.84 &= 150 \cdot 75 = 11250 \\ x &= 11250 + 1.84 = 11251.84. \end{align} Ответ: 11251,84.
3. (2 балла) Решение:
   Второй автомобиль выехал в 10:00. Обгон произошел в 13:00: \begin{align} \text{Время первого авто до встречи:} &\:4\:ч \quad (9:00 \rightarrow 13:00) \\ \text{Время второго авто до встречи:} &\:3\:ч \quad (10:00 \rightarrow 13:00) \\ \text{Путь до встречи:} &\:54 \cdot 4 = S = v_2 \cdot 3 \Rightarrow v_2 = 72\:км/ч. \\ \text{Расстояние } AB &\:72 \cdot 9\:ч = 648\:км. \\ \text{Время первого авто:} &\:648 \div 54 = 12\:ч \Rightarrow 9:00 + 12\:ч = 21:00. \end{align} Ответ: в 21:00.
4. (3 балла) Решение:
   Пусть сторона квадрата \( x \). Периметры серых прямоугольников: \begin{align} 2(x + a) = 32 &\Rightarrow x + a = 16 \\ 2(x + b) = 18 &\Rightarrow x + b = 9 \\ \text{Периметр листа:} &\:2(a + b) = 2(16 -x + 9 -x) = 50\:см \\ \text{Площадь:} &\:16 \cdot 9 = 144\:см^2. \end{align} Ответ: \( P = 50\:см \), \( S = 144\:см^2 \).
5. (3 балла) Решение:
   Оптимальное распределение: \begin{align} \text{Оля:} &\:8\: пет,\:40\:кур \quad (5 \cdot 8 + 3 \cdot 40 = 160\:мин) \\ \text{Света:} &\:40\: пет \quad (4 \cdot 40 = 160\:мин). \end{align} Ответ: 160 минут.
6. (3 балла) Решение:
   Возраст Маши:
   \begin{align} \text{Оля (младшая):} &\:10\:лет \\ \text{Разница с Машей:} &\:4\:года \Rightarrow \:Маше\:14\:лет. \\ \text{Таня:} &\:на\:5\:лет\:старше\:Маши \Rightarrow\:19\:лет. \end{align} Ответ: Таня — 19 лет, Маша — 14 лет.
7. (3 балла) Решение:
   Пример расстановки (центральное число 4):
   
   \begin{equation} \begin{array}{ccc} & 9 & \\ 1 & 4 & 7 \\ & 2 & \\ \end{array} \quad \text{Суммы кругов:} \quad \begin{cases} 9 + 1 + 4 = 14 \\ 1 + 7 + 6 = 14 \\ 7 + 2 + 5 = 14 \end{cases} \end{equation} Ответ: например, 1, 2, 6, 7, 5, 9 в соответствующих позициях.