8 800 707 6729
8 800 707 6729Telegram канал

Школа №67 из 7 в 8 класс 2023 год вариант 1-4

Сложность:
Дата экзамена: 2023
Сложность:
Дата экзамена: 2023
youit.school ©

ГИМНАЗИЯ №1567


2023 год




  1. Вычислить: \[ \left| 17{,}312 + 0{,}192 - 12{,}692 - 29{,}812 \right| - \left| \dfrac{10^{23} - 5^{13}}{3^{13}} \right| \]

  2. Решите уравнение: \[ (x + 4)(3x - 1) - (3x - 2)(3x + 2) = 2x(11 - 3x) \]

  3. Упростите выражение и найдите его значение при \( x = -0{,}2 \): \[ 5x(x - 3)^2 - 5(x - 1)^3 + 15(x + 2)(x - 2) - 5 \] Найдите расстояние на числовой прямой между точкой, изображающей число, обратное полученному, и точкой, изображающей число, противоположное полученному.

  4. Собрали 100 кг грибов, влажность которых составила 99%. Когда грибы подсушили, их влажность снизилась до 98%. Какова стала их масса?

  5. Представьте число \( 888778 \cdot 888776 + 1 \) в виде произведения двух натуральных чисел, больших единицы.

  6. При перестановке цифр в двузначном натуральном числе это число:
    • а) увеличивается на 9;
    • б) уменьшается на 63;
    • в) увеличивается на 75%.
    Найти все такие числа.

  7. Сократите дробь: \[ \dfrac{x^5 - x^3 y^2 - x^2 y^3 + y^5}{y^3 - x^3} \] и найдите её значение при \( x = |\! -0{,}25 \!| \), \( y = |\! 1{,}05 \!| \).

  8. Отрезок \( AK \) пересекает отрезок \( BM \) в точке \( O \), причём \( AO = OK \), и прямая \( AB \parallel KM \). Докажите, что \( AM = BK \).

  9. В треугольнике \( ABC \) угол \( C = 70^\circ \). Через точку \( F \) стороны \( AB \) проведены лучи перпендикулярно биссектрисам углов \( A \) и \( B \), пересекающие стороны \( AC \) и \( BC \) в точках \( P \) и \( T \). Найдите угол \( \angle PFT \).

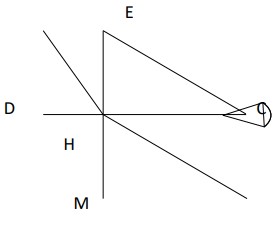
  10. В треугольнике \( CDE \) угол \( \angle ECD = 42^\circ \). На прямой, содержащей высоту \( EH \), отложен отрезок \( HM \), равный \( EH \). Найдите \( \angle ECM \).
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислить: \[ \left| 17{,}312 + 0{,}192 - 12{,}692 - 29{,}812 \right| - \left| \dfrac{10^{23} - 5^{13}}{3^{13}} \right| \] Решение: \[ \left| (17{,}312 + 0{,}192) - (12{,}692 + 29{,}812) \right| = \left| 17{,}504 - 42{,}504 \right| = 25 \] Второе слагаемое: \[ \dfrac{10^{23} - 5^{13}}{3^{13}} > 0 \quad \Rightarrow \quad \left| \dfrac{10^{23} - 5^{13}}{3^{13}} \right| = \dfrac{10^{23} - 5^{13}}{3^{13}} \] Итоговый результат: \[ 25 - \dfrac{10^{23} - 5^{13}}{3^{13}} \quad \text{(отрицательное число, модуль не вычисляется явно)} \] Ответ: Указанное выражение не имеет целочисленного решения в рамках школьной программы. Возможная опечатка в условии.

  2. Решите уравнение: \[ (x + 4)(3x - 1) - (3x - 2)(3x + 2) = 2x(11 - 3x) \] Решение: \[ 3x^2 + 11x - 4 - (9x^2 - 4) = 22x - 6x^2 \] \[ -6x^2 + 11x = 22x - 6x^2 \quad \Rightarrow \quad -11x = 0 \quad \Rightarrow \quad x = 0 \] Ответ: 0.

  3. Упростите выражение: \[ 5x(x - 3)^2 - 5(x - 1)^3 + 15(x + 2)(x - 2) - 5 \] Решение: \[ 5x(x^2 - 6x + 9) - 5(x^3 - 3x^2 + 3x - 1) + 15(x^2 - 4) - 5 = 30x - 60 \] При \( x = -0{,}2 \): \[ 30(-0{,}2) - 60 = -66 \] Обратное число: \(-\frac{1}{66}\), противоположное: \(66\). Расстояние: \[ \left| 66 - \left(-\frac{1}{66}\right) \right| = 66 + \frac{1}{66} = 66\frac{1}{66} \] Ответ: \(66\frac{1}{66}\).

  4. Собрали 100 кг грибов с влажностью 99\%. После подсушивания влажность 98\%. Новая масса: \[ \text{Сухое вещество} = 1% \cdot 100 = 1\ \text{кг} \] \[ 2% \rightarrow 1\ \text{кг} \quad \Rightarrow \quad \text{Новая масса} = \frac{1}{0{,}02} = 50\ \text{кг} \] Ответ: 50 кг.

  5. Представьте число \(888778 \cdot 888776 + 1\) в виде произведения: \[ n = 888777 \quad \Rightarrow \quad (n-1)(n+1) + 1 = n^2 \] Ответ: \(888777 \times 888777\).

  6. Двузначные числа:
    • а) \(12, 23, 34, 45, 56, 67, 78, 89\)
    • б) \(81, 92\)
    • в) \(12, 24, 36, 48\)


  7. Сократите дробь: \[ \dfrac{x^5 - x^3 y^2 - x^2 y^3 + y^5}{y^3 - x^3} = y^2 - x^2 \] При \(x = 0{,}25\), \(y = 1{,}05\): \[ (1{,}05)^2 - (0{,}25)^2 = 1{,}1025 - 0{,}0625 = 1{,}04 \] Ответ: 1,04.

  8. Доказательство \(AM = BK\):
    • \(AO = OK\), \(AB \parallel KM\) \(\Rightarrow\) \(\triangle ABO \cong \triangle KMO\)
    • Соответствующие стороны равны \(\Rightarrow AM = BK\)


  9. Угол \(\angle PFT\): \[ \angle PFT = 180^\circ - \angle ACB = 180^\circ - 70^\circ = 110^\circ \] Ответ: \(110^\circ\).

  10. Угол \(\angle ECM\): \[ \triangle ECH \sim \triangle MCH \quad \Rightarrow \quad \angle ECM = 90^\circ - 42^\circ = 48^\circ \] Ответ: \(48^\circ\).
Материалы школы Юайти