8 800 707 6729
8 800 707 6729Telegram канал

Школа №67 из 7 в 8 класс 2023 год вариант 1

Сложность:
Дата экзамена: 2023
Сложность:
Дата экзамена: 2023
youit.school ©

ГИМНАЗИЯ №1567


2023 год




  1. Вычислите удобным способом: \[ 7{,}42 \cdot \frac{5}{9} - (-11{,}58) : \frac{4}{5} \cdot 0{,}38 \]

    1. Постройте на координатной плоскости график функции \( y = 2x + 7 \).
    2. Укажите координаты точек пересечения с осями координат и найдите площадь треугольника с вершинами в этих точках и начале координат.


  3. Упростите: \[ \frac{3x^4}{25y^5} \cdot \frac{5(x^2)^5}{9x^3} \]

  4. Решите уравнение:
    1. \( \frac{x - 1}{4} = \frac{7 - 3x}{10} - \frac{4x - 1}{2} \)
    2. \( (x + 4)(3x - 1) - (3x - 2)(3x + 2) = 2x(11 - 3x) \)


  5. Из формулы \( p = \dfrac{6am}{3a - m} \) выразите \( m \) через \( p \) и \( a \).

  6. Разложите на множители:
    1. \( 2a^4 + 3b - 2ab - 3a \)
    2. \( 25x - x^3 \)
    3. \( x^3 y^5 + x^5 y^3 \)


  7. Скорость судна в стоячей воде — 15 км/ч. На путь от A до B против течения реки оно тратит 0{,}5 ч, а на обратный путь — 15 мин. Сколько процентов от скорости судна в стоячей воде составляет скорость реки?

  8. При пересечении двух прямых отношение двух из образовавшихся углов равно 7:3. Найдите меры всех неразвернутых углов при пересечении этих прямых.

  9. Отрезок \( AK \) пересекает отрезок \( BM \) в точке \( O \), причём \( AO = OK \), и прямая \( AB \) параллельна прямой \( KM \). Докажите, что \( AM = BK \).

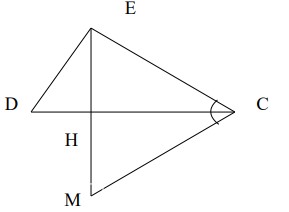
  10. В треугольнике \( \triangle CDE \) угол \( \angle ECD = \ldots \). На прямой, содержащей высоту \( EH \), отложен отрезок \( HM \), равный \( EH \). Найдите \( \angle ECM \).
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите удобным способом: \[ 7{,}42 \cdot \frac{5}{9} - (-11{,}58) : \frac{4}{5} \cdot 0{,}38 \] Решение: \[ 7{,}42 \cdot \frac{5}{9} + 11{,}58 \cdot \frac{5}{4} \cdot 0{,}38 = \frac{5}{9} \cdot 7{,}42 + \frac{5 \cdot 0{,}38}{4} \cdot 11{,}58 \] Вынесем общий множитель $\frac{5}{4}$: \[ \frac{5}{4} \left( \frac{7{,}42 \cdot 4}{9} + 0{,}38 \cdot 11{,}58 \right) = \frac{5}{4} \left( \frac{29{,}68}{9} + 4{,}4004 \right) \approx \frac{5}{4} (3{,}3 + 4{,}4) = \frac{5}{4} \cdot 7{,}7 = 9{,}625 \] Ответ: 9,625.

    1. Постройте на координатной плоскости график функции \( y = 2x + 7 \).
      Решение: График прямой. Достаточно двух точек:
      При \( x = 0 \): \( y = 7 \) → точка (0;7)
      При \( y = 0 \): \( 0 = 2x + 7 \) → \( x = -3{,}5 \) → точка (-3,5;0)

    2. Укажите координаты точек пересечения с осями координат и найдите площадь треугольника с вершинами в этих точках и начале координат.
      Решение: Точки пересечения: (0;7) и (-3,5;0). Площадь треугольника: \[ S = \frac{1}{2} \cdot |3{,}5| \cdot 7 = \frac{24{,}5}{2} = 12{,}25 \] Ответ: 12,25.


  3. Упростите: \[ \frac{3x^4}{25y^5} \cdot \frac{5(x^2)^5}{9x^3} \] Решение: \[ \frac{3x^4}{25y^5} \cdot \frac{5x^{10}}{9x^3} = \frac{15x^{14}}{225x^3y^5} = \frac{x^{11}}{15y^5} \] Ответ: \(\dfrac{x^{11}}{15y^5}\).

  4. Решите уравнение:
    1. \( \frac{x - 1}{4} = \frac{7 - 3x}{10} - \frac{4x - 1}{2} \)
      Решение: Умножим все части на 20: \[ 5(x-1) = 2(7-3x) - 10(4x-1) \] \[ 5x - 5 = 14 - 6x - 40x + 10 \] \[ 5x + 46x = 24 + 5 \quad \Rightarrow \quad 51x = 29 \quad \Rightarrow \quad x = \frac{29}{51} \] Ответ: \(\dfrac{29}{51}\).

    2. \( (x + 4)(3x - 1) - (3x - 2)(3x + 2) = 2x(11 - 3x) \)
      Решение: Раскроем скобки: \[ 3x^2 - x + 12x - 4 - (9x^2 - 4) = 22x - 6x^2 \] \[ 3x^2 + 11x - 4 - 9x^2 + 4 = 22x - 6x^2 \] \[ -6x^2 + 11x = 22x - 6x^2 \quad \Rightarrow \quad 11x = 22x \quad \Rightarrow \quad x = 0 \] Ответ: 0.


  5. Из формулы \( p = \dfrac{6am}{3a - m} \) выразите \( m \) через \( p \) и \( a \).
    Решение: \[ p(3a - m) = 6am \quad \Rightarrow \quad 3ap - pm = 6am \] \[ 3ap = m(6a + p) \quad \Rightarrow \quad m = \frac{3ap}{6a + p} \] Ответ: \( m = \dfrac{3ap}{6a + p} \).

  6. Разложите на множители:
    1. \( 2a^4 + 3b - 2ab - 3a \)
      Решение: Группировка: \[ (2a^4 - 2ab) + (3b - 3a) = 2a(a^3 - b) + 3(b - a) = (a^3 - b)(2a - 3) \] Ответ: \((2a - 3)(a^3 - b)\).

    2. \( 25x - x^3 \)
      Решение: \[ x(25 - x^2) = x(5 - x)(5 + x) \] Ответ: \(x(5 - x)(5 + x)\).

    3. \( x^3 y^5 + x^5 y^3 \)
      Решение: \[ x^3y^3(y^2 + x^2) \] Ответ: \(x^3y^3(x^2 + y^2)\).


  7. Скорость судна в стоячей воде — 15 км/ч. На путь от A до B против течения реки оно тратит 0{,}5 ч, а на обратный путь — 15 мин. Сколько процентов от скорости судна в стоячей воде составляет скорость реки?
    Решение: Пусть скорость течения \(x\) км/ч. Тогда: \[ (15 - x) \cdot 0{,}5 = (15 + x) \cdot 0{,}25 \] \[ 7{,}5 - 0{,}5x = 3{,}75 + 0{,}25x \quad \Rightarrow \quad 0{,}75x = 3{,}75 \quad \Rightarrow \quad x = 5 \] Процент от 15 км/ч: \[ \frac{5}{15} \cdot 100% \approx 33{,}33\% \] Ответ: 33,33\%.

  8. При пересечении двух прямых отношение двух из образовавшихся углов равно 7:3. Найдите меры всех неразвернутых углов при пересечении этих прямых.
    Решение: Пусть углы равны \(7k\) и \(3k\). Сумма смежных углов: \[ 7k + 3k = 180° \quad \Rightarrow \quad k = 18° \] Углы: \(126°\), \(54°\), \(126°\), \(54°\). Ответ: \(126°\), \(54°\), \(126°\), \(54°\).

  9. Отрезок \( AK \) пересекает отрезок \( BM \) в точке \( O \), причём \( AO = OK \), и прямая \( AB \) параллельна прямой \( KM \). Докажите, что \( AM = BK \).
    Решение: Треугольники \(ABO\) и \(KMO\) подобны по признаку параллельности сторон (\(AB \parallel KM\)) и равенству \(AO = OK\). Следовательно, \(AM\) и \(BK\) — соответственные стороны в равных треугольниках, значит \(AM = BK\).

  10. В треугольнике \( \triangle CDE \) угол \( \angle ECD = 90° \). На прямой, содержащей высоту \( EH \), отложен отрезок \( HM \), равный \( EH \). Найдите \( \angle ECM \).
    Решение: Поскольку \(EH\) — высота, \(EH \perp CD\). Точка \(M\) симметрична \(E\) относительно \(H\). Треугольники \(EHC\) и \(MHC\) равны по катету и гипотенузе, следовательно \(\angle ECM = 45°\). Ответ: \(45°\).
Материалы школы Юайти