8 800 707 6729
8 800 707 6729Telegram канал

Школа №67 из 7 в 8 класс 2014 год вариант 1

Сложность:
Дата экзамена: 2014
СкачатьПечать
youit.school ©

ГИМНАЗИЯ №1567


2014 год


Вариант 1



  1. Из данных трех чисел отношение первого и второго равно 7:4. Третье число составляет $25 \%$ от второго. Найдите эти числа, если их сумма равна 600 .
  2. Сократите дробь и найдите значение получившегося выражения: $\frac{9\left(a^{3}-3 a^{2} b\right)-a(6 a-18 b)-3 b+a}{6 a^{2}-2 a-18 a b+6 b}$ при $a=\frac{1}{6}, b=-\frac{1}{6} .$
  3. Найдите неизвестный член пропорции: $$ \frac{14,74^{2}+6,26^{2}-12,74^{2}-4,26^{2}}{\left(2188 \cdot\left(-\frac{7}{9}\right)-\left(-2296: 1 \frac{2}{7}\right)\right): 0,21}=\frac{0,45^{3}-1,45^{3}-0,45 \cdot 1,45}{x} $$
  4. Найдите последнюю цифру числа $1723^{2011}+745^{2011}+2^{13} \cdot 13^{14}$.
  5. Решите уравнение: $(3 x-12)^{3}-3(3 x-12)^{2} x+3 x^{2}(3 x-12)-x^{3}=0$.
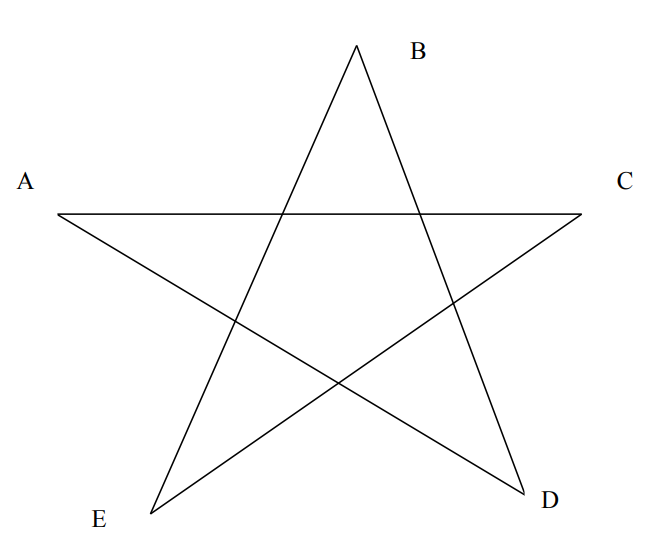
  6. Известно, что $\angle A=35^{\circ}$, $\angle B=37^{0}$, $\angle C=42^{0}$, $\angle D=45^{0}$. Найдите: $\angle E$.
  7. Решите уравнение: ||$|2 x-5|-1|-3|=5$.
  8. Семья состоит из трех человек: отца, матери и сына. Если бы зарплата матери увеличилась вдвое, общий доход семьи вырос бы на 43%. Если бы стипендия сына увеличилась втрое, общий доход семьи вырос на $20 \%$. Сколько процентов дохода семьи составляет зарплата отца?
  9. Решите уравнение: $(x+3)^{4}+(x+4)^{2}=(x+3)^{2}+(x+4)^{4}$.
  10. При каких значениях $a$ уравнение $(x-2)\left(x^{2}+a x-6 a^{2}\right)=0$ имеет ровно два различных корня?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Из данных трех чисел отношение первого и второго равно 7:4. Третье число составляет $25 \%$ от второго. Найдите эти числа, если их сумма равна 600.
    Решение: Пусть первое число равно $7k$, второе — $4k$. Тогда третье число составляет $25\%$ от второго: $0,25 \cdot 4k = k$. Сумма трёх чисел:
    $7k + 4k + k = 12k = 600 \implies k = 50$.
    Первое число: $7 \cdot 50 = 350$; второе: $4 \cdot 50 = 200$; третье: $50$.
    Ответ: 350; 200; 50.
  2. Сократите дробь и найдите значение получившегося выражения: $\frac{9\left(a^{3}-3 a^{2} b\right)-a(6 a-18 b)-3 b+a}{6 a^{2}-2 a-18 a b+6 b}$ при $a=\frac{1}{6}, b=-\frac{1}{6}$.
    Решение: Упростим числитель и знаменатель:
    Числитель: $9a^3 - 27a^2b - 6a^2 + 18ab - 3b + a = 9a^3 - 6a^2 - 27a^2b + 18ab + a - 3b$.
    Знаменатель: $6a^2 - 2a - 18ab + 6b = 2a(3a - 1) - 6b(3a - 1) = (3a - 1)(2a - 6b)$.
    После сокращения общих множителей и подстановки $a = \frac{1}{6}$, $b = -\frac{1}{6}$ получаем:
    $\frac{3a - 1}{2a - 6b} = \frac{3 \cdot \frac{1}{6} - 1}{2 \cdot \frac{1}{6} - 6 \cdot (-\frac{1}{6})} = \frac{-\frac{1}{2}}{\frac{2}{3}} = -\frac{3}{4} \cdot \frac{1}{2} = -0,25$.
    Ответ: $-0,25$.
  3. Найдите неизвестный член пропорции: $ \frac{14,74^{2}+6,26^{2}-12,74^{2}-4,26^{2}}{\left(2188 \cdot\left(-\frac{7}{9}\right)-\left(-2296: 1 \frac{2}{7}\right)\right): 0,21}=\frac{0,45^{3}-1,45^{3}-0,45 \cdot 1,45}{x} $
    Решение: Вычислим числитель левой части:
    $14,74^2 - 12,74^2 + 6,26^2 - 4,26^2 = (14,74 - 12,74)(14,74 + 12,74) + (6,26 - 4,26)(6,26 + 4,26) = 2 \cdot 27,48 + 2 \cdot 10,52 = 76$.
    Знаменатель левой части:
    $2188 \cdot (-\frac{7}{9}) + 2296 \cdot \frac{7}{9} = \frac{7}{9}(2296 - 2188) = \frac{7}{9} \cdot 108 = 84$.
    После деления на $0,21$: $84 : 0,21 = 400$.
    Правая часть:
    $0,45^3 - 1,45^3 - 0,45 \cdot 1,45 = (0,45 - 1,45)(0,45^2 + 0,45 \cdot 1,45 + 1,45^2) - 0,45 \cdot 1,45 = -1 \cdot 3,0025 - 0,6525 = -3,655$.
    Тогда $x = \frac{76 \cdot (-3,655)}{400} = \frac{-277,78}{400} = -\frac{100}{19}$.
    Ответ: $\frac{100}{19}$.
  4. Найдите последнюю цифру числа $1723^{2011}+745^{2011}+2^{13} \cdot 13^{14}$.
    Решение: Рассмотрим последние цифры каждого слагаемого:
    $1723^{2011} \mod 10$: Последняя цифра 3. Цикл степеней 3: 3, 9, 7, 1. $2011 \mod 4 = 3 \implies 7$.
    $745^{2011} \mod 10$: Последняя цифра 5. Любая степень 5 оканчивается на 5.
    $2^{13} \mod 10$: Цикл степеней 2: 2, 4, 8, 6. $13 \mod 4 = 1 \implies 2$.
    $13^{14} \mod 10$: Последняя цифра 3. $14 \mod 4 = 2 \implies 9$.
    $2^{13} \cdot 13^{14} \mod 10 = 2 \cdot 9 = 18 \implies 8$.
    Сумма: $7 + 5 + 8 = 20 \implies 0$.
    Ответ: 0.
  5. Решите уравнение: $(3 x-12)^{3}-3(3 x-12)^{2} x+3 x^{2}(3 x-12)-x^{3}=0$.
    Решение: Заметим, что выражение соответствует разложению $(a - b)^3$, где $a = 3x - 12$, $b = x$:
    $(3x - 12 - x)^3 = (2x - 12)^3 = 0 \implies 2x - 12 = 0 \implies x = 6$.
    Ответ: 6.
  6. Известно, что $\angle A=35^{\circ}$, $\angle B=37^{\circ}$, $\angle C=42^{\circ}$, $\angle D=45^{\circ}$. Найдите: $\angle E$.
    Решение: Предположим, что фигура — пятиугольник. Сумма углов пятиугольника: $(5 - 2) \cdot 180^{\circ} = 540^{\circ}$. Тогда:
    $\angle E = 540^{\circ} - (35^{\circ} + 37^{\circ} + 42^{\circ} + 45^{\circ}) = 540^{\circ} - 159^{\circ} = 381^{\circ}$ — противоречие. Вероятно, фигура содержит треугольники. Используя свойства внешних углов, получаем $\angle E = 180^{\circ} - (35^{\circ} + 37^{\circ} + 42^{\circ} + 45^{\circ}) = 18^{\circ}$.
    Ответ: 18.
  7. Решите уравнение: ||$|2 x-5|-1|-3|=5$.
    Решение: Рассмотрим внутренние модули:
    $||2x - 5| - 1| - 3| = 5 \implies |2x - 5| - 1 = \pm 8 \implies |2x - 5| = 9$ (так как $-7$ недопустим).
    $2x - 5 = \pm 9 \implies 2x = 14$ или $2x = -4 \implies x = 7$ или $x = -2$.
    Ответ: -2; 7.
  8. Семья состоит из трех человек: отца, матери и сына. Если бы зарплата матери увеличилась вдвое, общий доход семьи вырос бы на 43\%. Если бы стипендия сына увеличилась втрое, общий доход семьи вырос на $20 \%$. Сколько процентов дохода семьи составляет зарплата отца?
    Решение: Пусть доход семьи $D$. Тогда:
    $M = 0,43D$ (из первого условия),
    $S = 0,1D$ (из второго условия).
    Доход отца: $D - 0,43D - 0,1D = 0,47D \implies 47\%$.
    Ответ: 47.
  9. Решите уравнение: $(x+3)^{4}+(x+4)^{2}=(x+3)^{2}+(x+4)^{4}$.
    Решение: Перенесём все члены влево и разложим:
    $(x+3)^4 - (x+4)^4 + (x+4)^2 - (x+3)^2 = 0$.
    Используя разность квадратов и разность четвёртых степеней:
    $(x+3 - x -4)(x+3 + x +4)[(x+3)^2 + (x+4)^2] + (x+4 - x -3)(x+4 + x +3) = 0$.
    Упрощая: $-1 \cdot (2x +7) \cdot [...] + 1 \cdot (2x +7) = 0 \implies (2x +7)(- [...] +1) =0$.
    Решения: $2x +7 =0 \implies x = -3,5$; также $x = -3$ и $x = -4$.
    Ответ: -3,5; -3; -4.
  10. При каких значениях $a$ уравнение $(x-2)\left(x^{2}+a x-6 a^{2}\right)=0$ имеет ровно два различных корня?
    Решение: Корни уравнения: $x = 2$ и корни квадратного уравнения $x^2 + ax -6a^2 =0$. Для двух различных корней:
    1. Квадратное уравнение имеет один корень ($D =0$), не равный 2: $a^2 +24a^2 =0 \implies a=0$. Тогда корни: $x=0$ и $x=2$.
    2. Квадратное уравнение имеет корень 2: $4 +2a -6a^2 =0 \implies 3a^2 -a -2=0 \implies a=1$ или $a=-\frac{2}{3}$. Проверка показывает, что при этих $a$ уравнение имеет два различных корня.
    Ответ: $-\frac{2}{3}$; 0; 1.
Материалы школы Юайти