Школа №67 из 7 в 8 класс 2014 год геометрия

ГИМНАЗИЯ №1567

2014 год

Геометрия

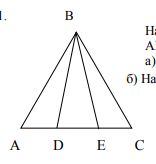
1. На данном рисунке $\triangle \mathrm{DBE}-$ равнобедренный с основанием $\mathrm{DE}$, $\mathrm{AD}=\mathrm{EC}$.
   1. Докажите, что $\Delta \mathrm{ABC}$ равнобедренный.
   2. Найдите $\angle \mathrm{BDE}$, если сумма $\angle \mathrm{BDA}$ и $\angle \mathrm{BEC}$ равна $230^{\circ} .$
   
   
2. В равнобедренном $\Delta \mathrm{ABC}$ с основанию АС проведена биссектриса ВD, равная 7 см. Найдите периметр $\Delta \mathrm{ABC}$, если периметр $\Delta \mathrm{ABD}$ равен $18 \mathrm{~cm}$.
3. Прямая d пересекает отрезок КМ в его середине точке В. Найти расстояние от точки К до прямой d, если расстояние от точки М до этой прямой равно 56 см.
4. В окружности с центром О и радиусом 2 дм проведена хорда АВ на расстоянии 10 см от ее центра. Найти углы треугольника ABO.
5. Даны две параллельные прямые $\mathrm{d}$ и b и секущая m. Биссектриса одного из внутренних углов, образованных прямыми d и $\mathrm{m}$, составляет с прямой b угол в $37^{\circ}$. Найти все углы, образованные прямыми d и b и секущей m.
6. Внешний угол треугольника равен $110^{\circ}$, а внутренние углы, не смежные с ним, относятся как $5: 6$. Найти углы треугольника.
7. Две стороны равнобедренного треугольника равны 2 см и 19 см. Найти периметр треугольника.
8. Два угла треугольника равны $22^{\circ}$ и $66^{\circ} .$ Середины сторон треугольника соединены отрезками, параллельными соответствующим сторонам. Найти углы треугольника, образованного этими отрезками.
9. В прямоугольном треугольнике биссектриса наибольшего угла пересекает гипотенузу под углом $80^{\circ} .$ Найдите острые угла данного треугольника.
10. В прямоугольном $\Delta A B C \angle B=90^{\circ}, A B=8 \mathrm{~cm}, A C=16 \mathrm{~cm}$. Найдите углы, которые образует высота $B H$ с катетами треугольника.

Решения задач

1. 1. Докажите, что $\Delta ABC$ равнобедренный.
      Решение:
      $\triangle DBE$ — равнобедренный с основанием $DE$, значит $DB = BE$.
      По условию $AD = EC$. Тогда:
      $AB = AD + DB = EC + BE = BC$.
      Следовательно, $\triangle ABC$ равнобедренный с основанием $AC$.
      
   2. Найдите $\angle BDE$, если сумма $\angle BDA$ и $\angle BEC$ равна $230^{\circ}$.
      Решение:
      $\angle BDA + \angle BEC = 230^{\circ}$.
      $\triangle ABD \cong \triangle CBE$ (по двум сторонам и углу: $AD = EC$, $AB = BC$, $\angle A = \angle C$).
      Значит, $\angle BDA = \angle BEC = \frac{230^{\circ}}{2} = 115^{\circ}$.
      В $\triangle BDE$: $\angle BDE = \angle BED = x$.
      $\angle DBE = 180^{\circ} - 2x$.
      В $\triangle ABD$: $\angle ABD = 180^{\circ} - \angle A - \angle BDA = 180^{\circ} - \angle A - 115^{\circ}$.
      Так как $\triangle ABC$ равнобедренный, $\angle A = \angle C$, а $\angle ABC = 180^{\circ} - 2\angle A$.
      Из $\angle ABD + \angle DBE = \angle ABC$:
      $(65^{\circ} - \angle A) + (180^{\circ} - 2x) = 180^{\circ} - 2\angle A$.
      Решая уравнение, получаем $x = 65^{\circ}$.
      Ответ: $\angle BDE = 65^{\circ}$.
2. В равнобедренном $\Delta ABC$ с основанием $AC$ проведена биссектриса $BD$, равная 7 см. Найдите периметр $\Delta ABC$, если периметр $\Delta ABD$ равен 18 см.
   Решение:
   Периметр $\Delta ABD$: $AB + BD + AD = 18$ см.
   $AB + 7 + \frac{AC}{2} = 18 \Rightarrow AB + \frac{AC}{2} = 11$.
   Периметр $\Delta ABC$: $2AB + AC = 2AB + 2(11 - AB) = 22$ см.
   Ответ: 22 см.
3. Прямая $d$ пересекает отрезок $KM$ в его середине точке $B$. Найти расстояние от точки $K$ до прямой $d$, если расстояние от точки $M$ до этой прямой равно 56 см.
   Решение:
   Точка $B$ — середина $KM$. При симметрии относительно $B$ точки $K$ и $M$ меняются местами, а прямая $d$ остается на месте.
   Следовательно, расстояния от $K$ и $M$ до $d$ равны.
   Ответ: 56 см.
4. В окружности с центром $O$ и радиусом 2 дм проведена хорда $AB$ на расстоянии 10 см от ее центра. Найти углы треугольника $ABO$.
   Решение:
   $OA = OB = 20$ см, $OH = 10$ см (расстояние от центра до хорды).
   В $\triangle AOH$: $\cos \angle AOH = \frac{OH}{OA} = \frac{10}{20} = 0,5 \Rightarrow \angle AOH = 60^{\circ}$.
   $\angle AOB = 2 \cdot 60^{\circ} = 120^{\circ}$.
   Углы при основании: $\frac{180^{\circ} - 120^{\circ}}{2} = 30^{\circ}$.
   Ответ: $30^{\circ}, 30^{\circ}, 120^{\circ}$.
5. Даны две параллельные прямые $d$ и $b$ и секущая $m$. Биссектриса одного из внутренних углов, образованных прямыми $d$ и $m$, составляет с прямой $b$ угол в $37^{\circ}$. Найти все углы, образованные прямыми $d$ и $b$ и секущей $m$.
   Решение:
   Биссектриса делит угол между $d$ и $m$ пополам.
   Угол между биссектрисой и $b$ равен $37^{\circ}$, значит угол между $d$ и $m$ равен $2 \cdot 37^{\circ} = 74^{\circ}$.
   Смежный угол: $180^{\circ} - 74^{\circ} = 106^{\circ}$.
   Ответ: $74^{\circ}, 106^{\circ}$.
6. Внешний угол треугольника равен $110^{\circ}$, а внутренние углы, не смежные с ним, относятся как $5: 6$. Найти углы треугольника.
   Решение:
   Внутренний угол, смежный с внешним: $180^{\circ} - 110^{\circ} = 70^{\circ}$.
   Остальные углы: $5x$ и $6x$.
   $5x + 6x + 70^{\circ} = 180^{\circ} \Rightarrow 11x = 110^{\circ} \Rightarrow x = 10^{\circ}$.
   Углы: $50^{\circ}, 60^{\circ}, 70^{\circ}$.
   Ответ: $50^{\circ}, 60^{\circ}, 70^{\circ}$.
7. Две стороны равнобедренного треугольника равны 2 см и 19 см. Найти периметр треугольника.
   Решение:
   Если боковые стороны 19 см, то периметр: $19 + 19 + 2 = 40$ см.
   Если боковые стороны 2 см, треугольник невозможен (2 + 2 < 19).
   Ответ: 40 см.
8. Два угла треугольника равны $22^{\circ}$ и $66^{\circ}$. Середины сторон треугольника соединены отрезками, параллельными соответствующим сторонам. Найти углы треугольника, образованного этими отрезками.
   Решение:
   Треугольник из средних линий подобен исходному с коэффициентом $\frac{1}{2}$.
   Углы сохраняются: $22^{\circ}, 66^{\circ}, 92^{\circ}$.
   Ответ: $22^{\circ}, 66^{\circ}, 92^{\circ}$.
9. В прямоугольном треугольнике биссектриса наибольшего угла пересекает гипотенузу под углом $80^{\circ}$. Найдите острые углы данного треугольника.
   Решение:
   Биссектриса прямого угла делит его на $45^{\circ}$.
   Угол между биссектрисой и гипотенузой $80^{\circ}$.
   В треугольнике с углами $80^{\circ}$ и $45^{\circ}$ третий угол: $180^{\circ} - 80^{\circ} - 45^{\circ} = 55^{\circ}$.
   Острые углы исходного треугольника: $35^{\circ}$ и $55^{\circ}$.
   Ответ: $35^{\circ}, 55^{\circ}$.
10. В прямоугольном $\Delta ABC$ $\angle B = 90^{\circ}$, $AB = 8$ см, $AC = 16$ см. Найдите углы, которые образует высота $BH$ с катетами треугольника.
    Решение:
    По теореме Пифагора: $BC = \sqrt{AC^2 - AB^2} = 8\sqrt{3}$ см.
    Высота $BH = \frac{AB \cdot BC}{AC} = 4\sqrt{3}$ см.
    В $\triangle ABH$: $\cos \angle ABH = \frac{AH}{AB} = \frac{4}{8} = 0,5 \Rightarrow \angle ABH = 60^{\circ}$.
    Угол между $BH$ и $BC$: $90^{\circ} - 60^{\circ} = 30^{\circ}$.
    Ответ: $30^{\circ}, 60^{\circ}$.