Школа №67 из 7 в 8 класс 2005 год вариант 1

ГИМНАЗИЯ №1567

2005 год

Вариант 1

1. Вычислить: $\frac{0,03+0,07:\left(1 \frac{7}{24}+\frac{7}{30}-2 \frac{9}{40}\right)+\frac{7}{36} \cdot \frac{18}{35}}{-0,1^{2}}$.
2. Найдите положительное число, если его квадрат равен $1566 \cdot 1568+1 .$
3. В комнате было 11 человек, причем их средний возраст составлял 22 года. После того, как один человек ушел из комнаты, средний возраст оставшихся составил 21 год. Сколько лет человеку, который ушел?
4. Найти нечетное простое число $\mathrm{n}$, такое, что $\left(8^{7}+2^{19}+4^{9}\right) \vdots \mathrm{n}$.
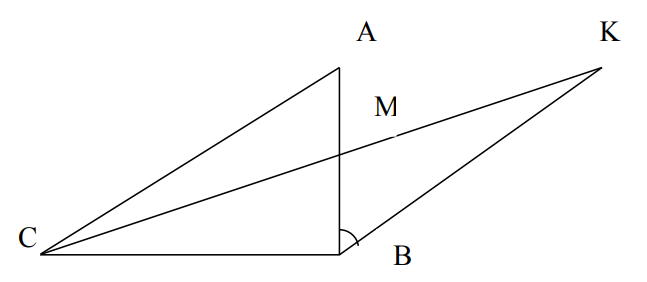
5. В треугольнике $\mathrm{ABC} \quad \angle \mathrm{A}: \angle \mathrm{B}: \angle \mathrm{C}=3: 5: 2$. На прямой, содержащей медиану СМ, отложен отрезок МК, равный СМ. Найти $\angle \mathrm{ABK}$.
   
6. Пешеход половину пути шел со скоростью 3 км/ч, а другую половину пути со скоростью 5 км/ч. Найти длину всего пути, пройденного пешеходом, если всего он находился в пути 8 часов?
7. Из двух положительных чисел одно увеличили на $1 \%$, другое на $4 \%$ при этом их сумма увеличилась на 3 \%. Найти большее из этих чисел, если меньшее равно $8 .$
8. Решить одно из уравнений (по выбору):
   1. $49(x-1)^{2}+14(x-1)+1=0 ;$
   2. $|x+y-z|+(\mathrm{y}-3)^{2}+(2 x-y)^{4}=0$ (относительно $\left.x, y, z\right)$.
9. В равнобедренном треугольнике $A B C$ с основанием $A B$ проведены биссектрисы $A A_{1}$ и $B B_{1}$, которые пересекаются в точке О. Найти углы треугольника $A O B_{1}$, если один из углов треугольника $A B C$ на $30^{\circ}$ больше другого. Рассмотреть не менее двух случаев.
10. Найти какое-либо натуральное число, которое при делении на каждое из чисел $2,3,4,5,6$ дает остаток 1 , если на 7 это число делится нацело.

Решения задач

1. Вычислить: $\frac{0,03+0,07:\left(1 \frac{7}{24}+\frac{7}{30}-2 \frac{9}{40}\right)+\frac{7}{36} \cdot \frac{18}{35}}{-0,1^{2}}$.
   Решение:
   Переведём смешанные числа в неправильные дроби:
   $1 \frac{7}{24} = \frac{31}{24}$, $2 \frac{9}{40} = \frac{89}{40}$.
   Найдём сумму в скобках:
   $\frac{31}{24} + \frac{7}{30} - \frac{89}{40} = \frac{155}{120} + \frac{28}{120} - \frac{267}{120} = -\frac{84}{120} = -\frac{7}{10}$.
   Вычислим деление:
   $0,07 : \left(-\frac{7}{10}\right) = -0,1$.
   Умножим дроби:
   $\frac{7}{36} \cdot \frac{18}{35} = \frac{1}{10} = 0,1$.
   Сложим части числителя:
   $0,03 + (-0,1) + 0,1 = 0,03$.
   Знаменатель:
   $-0,1^{2} = -0,01$.
   Итог:
   $\frac{0,03}{-0,01} = -3$.
   Ответ: $-3$.
2. Найдите положительное число, если его квадрат равен $1566 \cdot 1568+1 .$
   Решение:
   Заметим, что $1566 = 1567 - 1$, $1568 = 1567 + 1$.
   Тогда:
   $1566 \cdot 1568 + 1 = (1567 - 1)(1567 + 1) + 1 = 1567^{2} - 1 + 1 = 1567^{2}$.
   Ответ: 1567.
3. В комнате было 11 человек, причем их средний возраст составлял 22 года. После того, как один человек ушел из комнаты, средний возраст оставшихся составил 21 год. Сколько лет человеку, который ушел?
   Решение:
   Общий возраст 11 человек: $11 \cdot 22 = 242$ года.
   Общий возраст 10 человек: $10 \cdot 21 = 210$ лет.
   Возраст ушедшего: $242 - 210 = 32$ года.
   Ответ: 32.
4. Найти нечетное простое число $\mathrm{n}$, такое, что $\left(8^{7}+2^{19}+4^{9}\right) \vdots \mathrm{n}$.
   Решение:
   Упростим выражение:
   $8^{7} = 2^{21}$, $4^{9} = 2^{18}$.
   Тогда сумма: $2^{21} + 2^{19} + 2^{18} = 2^{18}(2^{3} + 2^{1} + 1) = 2^{18} \cdot 11$.
   Ответ: 11.
5. В треугольнике $\mathrm{ABC} \quad \angle \mathrm{A}: \angle \mathrm{B}: \angle \mathrm{C}=3: 5: 2$. На прямой, содержащей медиану СМ, отложен отрезок МК, равный СМ. Найти $\angle \mathrm{ABK}$.
   Решение:
   Сумма углов: $3x + 5x + 2x = 10x = 180^{\circ} \Rightarrow x = 18^{\circ}$.
   Углы: $\angle A = 54^{\circ}$, $\angle B = 90^{\circ}$, $\angle C = 36^{\circ}$.
   Треугольник $ABC$ — прямоугольный. Медиана $CM = \frac{1}{2}AB$. Точка $K$ симметрична $C$ относительно $M$, значит $ABK$ — параллелограмм. Угол $\angle ABK = 180^{\circ} - \angle BAC = 126^{\circ}$.
   Ответ: $126^{\circ}$.
6. Пешеход половину пути шел со скоростью 3 км/ч, а другую половину пути со скоростью 5 км/ч. Найти длину всего пути, пройденного пешеходом, если всего он находился в пути 8 часов?
   Решение:
   Пусть $S$ — весь путь. Время:
   $\frac{S/2}{3} + \frac{S/2}{5} = 8$.
   $\frac{S}{6} + \frac{S}{10} = 8 \Rightarrow \frac{8S}{30} = 8 \Rightarrow S = 30$ км.
   Ответ: 30 км.
7. Из двух положительных чисел одно увеличили на $1 \%$, другое на $4 \%$ при этом их сумма увеличилась на 3 \%. Найти большее из этих чисел, если меньшее равно $8 .$
   Решение:
   Пусть большее число $x$. Уравнение:
   $8 \cdot 1,01 + x \cdot 1,04 = (8 + x) \cdot 1,03$.
   $8,08 + 1,04x = 8,24 + 1,03x \Rightarrow 0,01x = 0,16 \Rightarrow x = 16$.
   Ответ: 16.
8. Решить уравнение: $49(x-1)^{2}+14(x-1)+1=0$.
   Решение:
   Замена $y = x - 1$:
   $49y^{2} + 14y + 1 = 0$.
   Дискриминант: $14^{2} - 4 \cdot 49 \cdot 1 = 0$.
   Корень: $y = -\frac{14}{2 \cdot 49} = -\frac{1}{7}$.
   $x - 1 = -\frac{1}{7} \Rightarrow x = \frac{6}{7}$.
   Ответ: $x = \frac{6}{7}$.
9. В равнобедренном треугольнике $A B C$ с основанием $A B$ проведены биссектрисы $A A_{1}$ и $B B_{1}$, которые пересекаются в точке О. Найти углы треугольника $A O B_{1}$, если один из углов треугольника $A B C$ на $30^{\circ}$ больше другого. Рассмотреть не менее двух случаев.
   Решение:
   Случай 1: Угол при вершине $C$ на $30^{\circ}$ больше.
   Углы: $\angle A = \angle B = 50^{\circ}$, $\angle C = 80^{\circ}$.
   Биссектрисы делят углы пополам: $\angle OAB_{1} = 25^{\circ}$, $\angle AB_{1}O = 25^{\circ}$, $\angle AOB_{1} = 130^{\circ}$.
   Случай 2: Угол при основании на $30^{\circ}$ больше.
   Углы: $\angle A = \angle B = 70^{\circ}$, $\angle C = 40^{\circ}$.
   Биссектрисы: $\angle OAB_{1} = 35^{\circ}$, $\angle AB_{1}O = 35^{\circ}$, $\angle AOB_{1} = 110^{\circ}$.
   Ответ: $25^{\circ}, 25^{\circ}, 130^{\circ}$ или $35^{\circ}, 35^{\circ}, 110^{\circ}$.
10. Найти какое-либо натуральное число, которое при делении на каждое из чисел $2,3,4,5,6$ дает остаток 1 , если на 7 это число делится нацело.
    Решение:
    Число $N = \text{НОК}(2,3,4,5,6) \cdot k + 1 = 60k + 1$.
    Найдём $k$: $60k + 1 \equiv 0 \mod 7 \Rightarrow 4k \equiv 6 \mod 7 \Rightarrow k = 5$.
    $N = 60 \cdot 5 + 1 = 301$.
    Ответ: 301.