Школа №67 из 4 в 5 класс 2023 год вариант 3

ГИМНАЗИЯ №1567

2023 год

Вариант 3

1. Реши уравнение:
   \[ \frac{186}{\left( \frac{x}{12} + 25 \right)} = 6 \]
   
   
2. Реши задачу:
   Караван прошёл по пустыне мимо путника и баобаба и идёт к роднику. В тот момент, когда от него до родника оставалось на 120 метров меньше, чем от родника до баобаба, от путника до баобаба было на 410 метров ближе, чем от путника до родника.
   Сколько в этот момент оставалось пройти каравану до родника?
   
   
3. Реши задачу:
   Мальчик и девочка носят воду в вёдрах из колодца. Бочка в 70 л наполнится, если мальчик выльет в неё 5 своих полных вёдер, а девочка добавит 6 своих.
   Бочка в 83 л наполнится, если мальчик выльет 6 своих, а девочка — 7 своих.
   Сколько раз им надо вместе сходить за водой, чтобы бочка в 100 л оказалась полной?
   
   
4. Реши задачу:
   Два бобра одновременно с двух сторон начали перегрызать осиновый ствол. Один бобр грыз со скоростью 5 см/ч. За час работы он догрыз одну треть ствола и ушёл домой. Другой бобр, трудясь в одиночестве 3 часа, догрыз осину до места, где её бросил первый.
   С какой скоростью грыз ствол второй бобр? Обоснуй свой ответ.
   
   
5. Перечисли все треугольники, которые есть на рисунке.
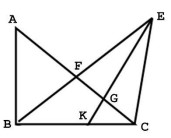   Образец: \( \triangle ABF, \ldots \)

Решения задач

1. Реши уравнение: \[ \frac{186}{\left( \frac{x}{12} + 25 \right)} = 6 \] Решение: \[ \frac{186}{\frac{x}{12} + 25} = 6 \quad \Big| \cdot \left(\frac{x}{12} + 25\right) \] \[ 186 = 6 \cdot \left(\frac{x}{12} + 25\right) \] \[ 186 = \frac{x}{2} + 150 \] \[ \frac{x}{2} = 36 \quad \Big| \cdot 2 \] \[ x = 72 \] Проверка: \(\frac{72}{12} + 25 = 6 + 25 = 31\), \(\frac{186}{31} = 6\).
   Ответ: 72.
   
   
2. Реши задачу:
   Пусть расстояние от родника до баобаба равно \(D\) метров. В момент времени, когда каравану осталось \(D - 120\) метров до родника, расстояние от путника до баобаба на 410 метров меньше, чем до родника. Составим уравнение: \[ (D - (D - 120)) + (D - 120) - (D - 120 - \text{путь до путника}) = 410 \] Упростим: \[ D - 240 = 410 \quad \Rightarrow \quad D = 650 \] Тогда каравану осталось пройти: \[ 650 - 120 = 530 \text{ метров} \] Ответ: 530 метров.
   
   
3. Реши задачу:
   Пусть объём ведра мальчика \(x\) литров, девочки \(y\) литров. Составим систему уравнений: \[ \begin{cases} 5x + 6y = 70 \\ 6x + 7y = 83 \end{cases} \] Решение: Умножим первое уравнение на 6, второе на 5: \[ \begin{cases} 30x + 36y = 420 \\ 30x + 35y = 415 \end{cases} \] Вычтем уравнения: \[ y = 5 \] Подставим \(y = 5\) в первое уравнение: \[ 5x + 30 = 70 \quad \Rightarrow \quad x = 8 \] Для заполнения 100 л: \[ 8a + 5b = 100 \] Минимальное \(a + b\) при целых \(a, b \geq 0\): \(a = 10\), \(b = 4\).
   Ответ: 14 раз.
   
   
4. Реши задачу:
   Пусть длина ствола \(L\). Первый бобр за час прогрыз: \[ \frac{L}{3} = 5 \text{ см/ч} \quad \Rightarrow \quad L = 15 \text{ см} \] Второй бобр грыз со скоростью \(v\) см/ч. За первый час вместе они прогрызли: \[ 5 + v \text{ см} \] Оставшаяся часть: \[ 15 - (5 + v) = 10 - v \] Второй бобр догрыз за 3 часа: \[ 3v = 10 - v \quad \Rightarrow \quad 4v = 10 \quad \Rightarrow \quad v = 2,5 \text{ см/ч} \] Ответ: 2,5 см/ч.
   
   
5. Перечисли все треугольники, которые есть на рисунке:
   \(\triangle ABF\), \(\triangle BCF\), \(\triangle CDF\), \(\triangle DEF\), \(\triangle EFA\), \(\triangle ABE\), \(\triangle BCD\), \(\triangle CDE\), \(\triangle ADE\), \(\triangle ACD\), \(\triangle BDF\), \(\triangle ACE\).
   Ответ: \(\triangle ABF\), \(\triangle BCF\), \(\triangle CDF\), \(\triangle DEF\), \(\triangle EFA\), \(\triangle ABE\), \(\triangle BCD\), \(\triangle CDE\), \(\triangle ADE\), \(\triangle ACD\), \(\triangle BDF\), \(\triangle ACE\).