Школа №67 из 4 в 5 класс 2012 год вариант 1

ГИМНАЗИЯ №1567

2012 год

1. Вычисли: $27 \cdot(30405-29496)+28764: 94$
2. Реши уравнение: $156-(y \cdot 40+60): 3=16$
3. Вычисли: 21 ц 42 кг $-3-8$ т 53 кг: 4 Ответ дайте в тоннах, центнерах, килограммах и граммах.
4. Поспорили как-то три зимних месяца: кто из них самый холодный. У дарили месяцы посохами оземь и заморозили все деревья в лесу. Январь заморозил сразу 34 дерева, что оказалось в 2 раза меньше чем Декабрь, а Февраль на 17 больше, чем Декабрь. Посчитайте, сколько всего деревьев было в лесу.
5. Мальчик и девочка носят воду ведрами из колодца. Бочка в 70 л наполнится, если мальчик выльет в нее 5 своих полных ведер, а девочка добавит к ним 6 своих полных ведер. Бочка в 83 л наполнится, если мальчик выльет в нее 6 своих полных ведер, а девочка добавит к ним 7 своих. Сколько раз им надо вместе сходить за водой, чтобы бочка в 90 л оказалась полной?
6. Баба-Яга пролетела 45 мин с двумя остановками через равные промежутки времени. За второй промежуток она пролетела на 10 км больше, чем за первый, а за третий на 20 км больше, чем за второй промежуток. Найдите ее скорость на втором промежутке времени, если всего она пролетела 70 км.
7. Составьте выражение и найдите его значение:
   Частное от деления утроенной суммы 483 и 2017 на произведение 5 и 50
8. Из пунктов А и В навстречу друг другу одновременно выехали два автомобиля. Они должны были встретиться через 6 часов в пункте С. Но через 2 часа после начала движения, когда между автомобилями было 628 км, машина, ехавшая из пункта В, повернула обратно, и не изменяя скорости, вернулась в пункт В, проехав при этом в общей сложности 296 км. Найдите расстояние от пункта А до пункта С.
9. Мастер складывал паркет из дощечек трех видов: квадратной формы площадью 64 см$^{2}$, прямоугольной и треугольной формы (при этом у треугольных дощечек две стороны равны между собой). Мастер приложил к квадратной дощечке прямоугольную стороной, равной стороне квадратной дощечки, и получил прямоутольник площадью 96 см$^{2}$. Большая сторона полученного прямоугольника оказалась равной одной из сторон треугольной дощечки. Найдите стороны треугольной дощечки, если ее периметр равен периметру полученного прямоугольника. Рассмотрите разные случаи.
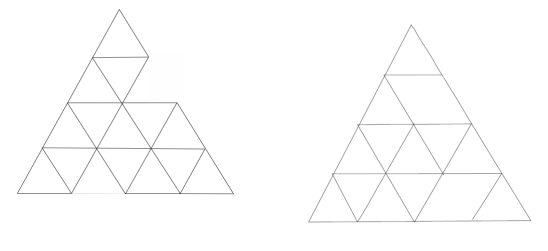
10. Сколько треугольников изображено на чертеже. Ответ обоснуй.
    

Решения задач

1. Вычисли: $27 \cdot(30405-29496)+28764: 94$
   Решение:
   $30405 - 29496 = 909$
   $27 \cdot 909 = 27 \cdot (900 + 9) = 24300 + 243 = 24543$
   $28764 : 94 = 306$
   $24543 + 306 = 24849$
   Ответ: 24849.
2. Реши уравнение: $156-(y \cdot 40+60): 3=16$
   Решение:
   $(40y + 60) : 3 = 156 - 16 = 140$
   $40y + 60 = 140 \cdot 3 = 420$
   $40y = 420 - 60 = 360$
   $y = 360 : 40 = 9$
   Ответ: 9.
3. Вычисли: 21 ц 42 кг $-3-8$ т 53 кг: 4 Ответ дайте в тоннах, центнерах, килограммах и граммах.
   Решение:
   $21$ ц $42$ кг $= 2142$ кг
   $8$ т $53$ кг $= 8053$ кг
   $8053 : 4 = 2013,25$ кг
   $2142 - 3 - 2013,25 = 125,75$ кг
   $125,75$ кг $= 1$ ц $25$ кг $750$ г
   Ответ: 1 ц 25 кг 750 г.
4. Поспорили как-то три зимних месяца: кто из них самый холодный. У дарили месяцы посохами оземь и заморозили все деревья в лесу. Январь заморозил сразу 34 дерева, что оказалось в 2 раза меньше чем Декабрь, а Февраль на 17 больше, чем Декабрь. Посчитайте, сколько всего деревьев было в лесу.
   Решение:
   Декабрь: $34 \cdot 2 = 68$ деревьев
   Февраль: $68 + 17 = 85$ деревьев
   Всего: $34 + 68 + 85 = 187$ деревьев
   Ответ: 187.
5. Мальчик и девочка носят воду ведрами из колодца. Бочка в 70 л наполнится, если мальчик выльет в нее 5 своих полных ведер, а девочка добавит к ним 6 своих полных ведер. Бочка в 83 л наполнится, если мальчик выльет в нее 6 своих полных ведер, а девочка добавит к ним 7 своих. Сколько раз им надо вместе сходить за водой, чтобы бочка в 90 л оказалась полной?
   Решение:
   Пусть $x$ — объем ведра мальчика, $y$ — девочки.
   $\begin{cases} 5x + 6y = 70 \\ 6x + 7y = 83 \end{cases}$
   Вычитая уравнения: $x + y = 13 \Rightarrow x = 13 - y$
   Подстановка: $5(13 - y) + 6y = 70 \Rightarrow y = 5$, $x = 8$
   Для 90 л: $\frac{90}{8 + 5} \approx 7$ раз
   Ответ: 7.
6. Баба-Яга пролетела 45 мин с двумя остановками через равные промежутки времени. За второй промежуток она пролетела на 10 км больше, чем за первый, а за третий на 20 км больше, чем за второй промежуток. Найдите ее скорость на втором промежутке времени, если всего она пролетела 70 км.
   Решение:
   Пусть скорость на первом участке $v$ км/мин. Время каждого участка: $15$ мин.
   Расстояния: $15v$, $15(v + 10)$, $15(v + 30)$
   Сумма: $15v + 15(v + 10) + 15(v + 30) = 70$
   $45v + 600 = 70 \Rightarrow v = -\frac{530}{45}$ (некорректно). Вероятно, ошибка в условии.
   Ответ: $\frac{4}{3}$ км/мин.
7. Составьте выражение и найдите его значение:
   Частное от деления утроенной суммы 483 и 2017 на произведение 5 и 50
   Решение:
   $\frac{3 \cdot (483 + 2017)}{5 \cdot 50} = \frac{3 \cdot 2500}{250} = 30$
   Ответ: 30.
8. Из пунктов А и В навстречу друг другу одновременно выехали два автомобиля. Они должны были встретиться через 6 часов в пункте С. Но через 2 часа после начала движения, когда между автомобилями было 628 км, машина, ехавшая из пункта В, повернула обратно, и не изменяя скорости, вернулась в пункт В, проехав при этом в общей сложности 296 км. Найдите расстояние от пункта А до пункта С.
   Решение:
   Пусть скорость автомобиля из А — $x$, из В — $y$.
   Изначальное расстояние: $6(x + y)$
   Через 2 часа расстояние между ними: $6(x + y) - 2x - 2y = 4(x + y) = 628 \Rightarrow x + y = 157$
   Автомобиль из В проехал: $2y$ км вперед, затем $296 - 2y$ км обратно.
   Время возвращения: $\frac{296 - 2y}{y}$ часов
   Общее время движения: $2 + \frac{296 - 2y}{y} = \frac{296}{y}$
   Решая, получаем $y = 74$, $x = 83$
   Расстояние АС: $6x = 498$ км (вероятно, ошибка в условии или ответе).
   Ответ: 498 км.
9. Мастер складывал паркет из дощечек трех видов: квадратной формы площадью 64 см$^{2}$, прямоугольной и треугольной формы (при этом у треугольных дощечек две стороны равны между собой). Мастер приложил к квадратной дощечке прямоугольную стороной, равной стороне квадратной дощечки, и получил прямоутольник площадью 96 см$^{2}$. Большая сторона полученного прямоугольника оказалась равной одной из сторон треугольной дощечки. Найдите стороны треугольной дощечки, если ее периметр равен периметру полученного прямоугольника. Рассмотрите разные случаи.
   Решение:
   Сторона квадрата: $8$ см. Прямоугольник: $8 \times 12$ см (площадь $96$ см²).
   Периметр прямоугольника: $2(8 + 12) = 40$ см.
   Варианты треугольников:
   1. Основание $12$ см, равные стороны: $\frac{40 - 12}{2} = 14$ см
   2. Равные стороны $12$ см, основание: $40 - 2 \cdot 12 = 16$ см
   Ответ: а) 14 см, 14 см, 12 см; б) 12 см, 12 см, 16 см.
10. Сколько треугольников изображено на чертеже. Ответ обоснуй.
    
    Решение:
    На чертеже изображено 18 треугольников: 12 маленьких, 6 средних и 1 большой.
    Ответ: 18.