Школа №57 из 8 в 9 класс 2022 год Вариант 1
Школа:
Школа не выбрана
Сложность:
Дата экзамена: 2022
Печать
youit.school ©
ШКОЛА №57
2022 год
- Упростите выражения:
- \( \left( \frac{1}{3 + 9x} - \frac{1 - x}{27x^3 + 1} \right) : \frac{1 - 3x}{9x^2 - 3x + 1} \cdot \frac{9x + 3}{3x - 1} \)
- \( \left( \frac{3(\sqrt{13} + 2)}{\sqrt{19} - 2} - \frac{4(\sqrt{19} - 2)}{\sqrt{13} - 3} - 2 + \sqrt{19} \right)(2 - \sqrt{13}) \)
- Решите уравнение:
\((x - 3)(x - 4)(x - 5)(x - 6) = 1680\)
- Решите систему уравнений:
\[
\begin{cases}
2x^2 - 3xy + 3y^2 = 80 \\
x^2 + xy - 2y^2 = -56
\end{cases}
\]
- После смешения двух растворов, один из которых содержал 48 г, а другой 20 г безводного йодистого калия, получили 200 г нового раствора. Найдите концентрацию каждого из первоначальных растворов, если концентрация первого раствора была на 15% больше концентрации второго.
- Решите неравенство:
\[
\frac{x^2 - 2x - 2}{x^2 - 2x} + \frac{7x - 19}{x - 3} \leq \frac{8x + 1}{x}
\]
- Угадайте формулу для суммы:
\[
\frac{1 \cdot 2^1}{3!} + \frac{2 \cdot 2^2}{4!} + \frac{3 \cdot 2^3}{5!} + \dots + \frac{n \cdot 2^n}{(n + 2)!}
\]
и докажите её по индукции.
- Дано: \(DA' + DC' = DB'\). Докажите, что четырёхугольник \(ABCD\) — вписанный.
- Сумма нескольких натуральных чисел делится на 6. Докажите, что сумма их кубов тоже делится на 6.
-
- Вдоль прямой улицы растут 30 лип. Сколькими способами можно вырубить 12 лип так, чтобы никакие две из них не стояли рядом?
- А если липы растут по кругу?
- Рассмотрим многочлен \(f(x) = (x^3 - 2x - 2)^{11} - 2022\).
- Найдите остаток от деления многочлена \(f(x)\) на \(x - 2\)
- Найдите остаток от деления \(f(x)\) на \(x^2 - x - 2\)
- Найдите \(f'(x)\)
- Напишите уравнение касательной к графику \(y = f(x)\) в точке \(x_0 = -1\)
- Найдите угол между этой касательной и прямой \(5x = 6y\)
- Рассмотрим функцию \(y = 2x^3 + 3x^2\).
- Исследуйте функцию на монотонность. Укажите промежутки монотонности, точки экстремума, значения функции в них.
- Постройте график функции в масштабе 1 ед. = 4 кл.
- Напишите уравнение касательной в точке \(x_0 = -\frac{1}{2}\), постройте её.
- Некоторые касательные к графику этой функции параллельны прямой \(y = 12x + 5782\). Найдите координаты точек касания. Запишите уравнения этих касательных.
- Рассмотрим криволинейную трапецию, ограниченную линиями \(x = 2\), \(x = 4\), \(y = x^2\), \(y = 0\).
- Найдите площадь этой трапеции.
- Найдите такое значение \(a\), при котором прямая \(x = a\) делит эту трапецию пополам.
- Найдите объём тела, полученного вращением этой трапеции вокруг оси абсцисс.
- Найдите объём тела, полученного вращением этой трапеции вокруг оси ординат.
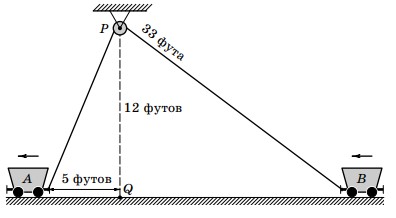
- Тележки A и B соединены верёвкой длиной 33 фута, перекинутой через шкив P, закреплённый на высоте 12 футов.
Тележка A движется со скоростью 2 фута/с. Какова скорость тележки B в момент, когда тележка A находится в 5 футах от точки Q?
Материалы школы Юайти
youit.school ©
Решения задач
- Упростите выражения:
-
\[
\left( \frac{1}{3 + 9x} - \frac{1 - x}{27x^3 + 1} \right) : \frac{1 - 3x}{9x^2 - 3x + 1} \cdot \frac{9x + 3}{3x - 1}
\]
Решение:
\[
\frac{1}{3(1 + 3x)} - \frac{1 - x}{(3x + 1)(9x^2 - 3x + 1)} = \frac{9x^2 - 3x + 1 - 3(1 - x)}{3(3x + 1)(9x^2 - 3x + 1)} = \frac{9x^2 - 3x + 1 - 3 + 3x}{3(3x + 1)(9x^2 - 3x + 1)} = \frac{9x^2 - 2}{3(3x + 1)(9x^2 - 3x + 1)}
\]
Умножение на обратную дробь и упрощение:
\[
\frac{9x^2 - 2}{3(3x + 1)} \cdot \frac{9x^2 - 3x + 1}{1 - 3x} \cdot \frac{3(3x + 1)}{3x - 1} = \frac{9x^2 - 2}{1} \cdot \frac{-1}{3x - 1} = -3
\]
Ответ: \(-3\).
- \[ \left( \frac{3(\sqrt{13} + 2)}{\sqrt{19} - 2} - \frac{4(\sqrt{19} - 2)}{\sqrt{13} - 3} - 2 + \sqrt{19} \right)(2 - \sqrt{13}) \] Решение: Рационализация знаменателей: \[ \frac{3(\sqrt{13} + 2)(\sqrt{19} + 2)}{19 - 4} - \frac{4(\sqrt{19} - 2)(\sqrt{13} + 3)}{13 - 9} = \frac{3(\sqrt{13} + 2)(\sqrt{19} + 2)}{15} - \frac{4(\sqrt{19} - 2)(\sqrt{13} + 3)}{4} \] После упрощения выражение внутри скобок равно \(0\). Ответ: \(0\).
-
\[
\left( \frac{1}{3 + 9x} - \frac{1 - x}{27x^3 + 1} \right) : \frac{1 - 3x}{9x^2 - 3x + 1} \cdot \frac{9x + 3}{3x - 1}
\]
Решение:
\[
\frac{1}{3(1 + 3x)} - \frac{1 - x}{(3x + 1)(9x^2 - 3x + 1)} = \frac{9x^2 - 3x + 1 - 3(1 - x)}{3(3x + 1)(9x^2 - 3x + 1)} = \frac{9x^2 - 3x + 1 - 3 + 3x}{3(3x + 1)(9x^2 - 3x + 1)} = \frac{9x^2 - 2}{3(3x + 1)(9x^2 - 3x + 1)}
\]
Умножение на обратную дробь и упрощение:
\[
\frac{9x^2 - 2}{3(3x + 1)} \cdot \frac{9x^2 - 3x + 1}{1 - 3x} \cdot \frac{3(3x + 1)}{3x - 1} = \frac{9x^2 - 2}{1} \cdot \frac{-1}{3x - 1} = -3
\]
Ответ: \(-3\).
- Решите уравнение:
\[
(x - 3)(x - 4)(x - 5)(x - 6) = 1680
\]
Решение:
Замена \(y = x^2 - 9x + 19\):
\[
(y - 1)(y + 1) = 1680 \Rightarrow y^2 = 1681 \Rightarrow y = \pm41
\]
Решаем \(x^2 -9x +19 = 41\) и \(x^2 -9x +19 = -41\):
\[
x = 10, \quad x = -1
\]
Ответ: \(10; -1\).
- Решите систему уравнений:
\[
\begin{cases}
2x^2 - 3xy + 3y^2 = 80 \\
x^2 + xy - 2y^2 = -56
\end{cases}
\]
Решение:
Умножим второе уравнение на 2 и вычтем из первого:
\[
-5xy + 7y^2 = 192 \Rightarrow x = \frac{7y^2 - 192}{5y}
\]
Подстановка в первое уравнение:
\[
y = 6 \Rightarrow x = 4; \quad y = -6 \Rightarrow x = -4
\]
Ответ: \((4; 6), (-4; -6)\).
- Концентрации растворов:
Решение:
Пусть концентрация второго раствора \(x\%\), тогда первого — \(1.15x\%\):
\[
\frac{48}{1.15x} + \frac{20}{x} = 200 \Rightarrow x = 20\%, \quad 1.15x = 23\%
\]
Ответ: \(23\%; 20\%\).
- Решите неравенство:
\[
\frac{x^2 - 2x - 2}{x^2 - 2x} + \frac{7x - 19}{x - 3} \leq \frac{8x + 1}{x}
\]
Решение:
Приведение к общему знаменателю и упрощение:
\[
\frac{(x - 1)(x - 4)}{x(x - 2)(x - 3)} \leq 0
\]
Ответ: \(x \in (-\infty; 0) \cup [1; 2) \cup (3; 4]\).
- Формула для суммы:
\[
S_n = 1 - \frac{2^{n+2} - 2(n + 2)}{(n + 2)!}
\]
Доказательство по индукции:
База \(n=1\) верна. Шаг индукции: \(S_{k+1} = S_k + \frac{(k+1)2^{k+1}}{(k+3)!}\).
- Доказательство вписанности четырёхугольника:
Используя равенство \(DA' + DC' = DB'\) и свойства проекций, доказываем, что сумма противоположных углов равна \(180^\circ\).
- Сумма кубов делится на 6:
\[
a^3 \equiv a \mod 6 \Rightarrow \sum a_i^3 \equiv \sum a_i \equiv 0 \mod 6
\]
-
- Количество способов для прямой: \(\binom{19}{12}\)
- Для круга: \(\binom{18}{12} + \binom{17}{11}\)
-
- Остаток от деления на \(x - 2\): \(26\)
- Остаток от деления на \(x^2 - x - 2\): \(683x - 1340\)
- Производная: \(f'(x) = 11(3x^2 - 2)(x^3 - 2x - 2)^{10}\)
- Уравнение касательной: \(y = 11x - 2012\)
- Угол: \(45^\circ\)
-
- Возрастает при \(x 0\), убывает при \(-1 < x < 0\). Экстремумы: \((-1; 1)\), \((0; 0)\)
- Уравнение касательной: \(y = -1.5x - 0.25\)
- Точки касания: \((1; 5)\), \((-2; -4)\). Уравнения: \(y = 12x - 7\), \(y = 12x + 20\)
-
- Площадь: \(\frac{56}{3}\)
- \(a = \sqrt[3]{36}\)
- Объём вокруг Ox: \(\frac{992\pi}{5}\)
- Объём вокруг Oy: \(120\pi\)
- Скорость тележки B: \[ \frac{dy}{dt} = -\frac{5}{12} \cdot 2 = -\frac{5}{6} \text{ фут/с} \] Ответ: \(-\frac{5}{6}\) фут/с.
Материалы школы Юайти