Школа №57 из 8 в 9 класс 2014 год Вариант 2

ШКОЛА №57

2014 год

Вариант 2

1. Кофе при жа́ренье теряет $12 \%$ своего веса. Сколько килограммов свежего кофе надо взять, чтобы получить 4,4 кг жареного?
2. Упростите алгебраические выражения:
   1. $\left(c-\frac{c^{3}+8}{2 c+c^{2}}\right) \cdot \frac{c}{(c-2)^{2}}+\frac{2}{2-c} ;$
   2. $(2-\sqrt{5}) \sqrt{9+4 \sqrt{5}}$.
3. Найдите знаки $a, b$, и знак дискриминанта квадратного трехчлена $y=a x^{2}+b x+c$, исходя из его графика:
   
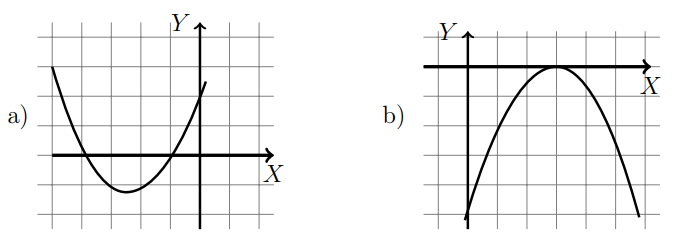
4. Решите систему $\left\{\begin{array}{l}x^{2}+y^{2}=5 \\ x^{3} y+x y^{3}=10\end{array}\right.$
5. В каждую клетку таблицы $3 \times 3$ произвольно ставят крестик или нолик.
   1. Сколькими способами можно заполнить эту таблицу?
   2. В скольких случаях в первом столбце будут стоять одни крестики?
   3. В скольких случаях по диагонали будут стоять одни нолики?
   4. В скольких случаях во втором столбце будет стоять ровно один крестик?
6. Из пункта А в пункт Б, расположенный в 24 км от А, одновременно отправились велосипедист и пешеход. Велосипедист прибыл в пункт Б на 4 часа раньше пешехода. Известно, что если бы велосипедист ехал с меньшей на 4 км/ч скоростью, то на путь из А в Б он затратил бы вдвое меньше времени, чем пешеход. Найдите скорость пешехода.
7. В равнобокую трапецию с основаниями 2 и 8 вписана окружность. Найдите ее радиус.

Решения задач

1. Кофе при жаренье теряет $12\%$ своего веса. Сколько килограммов свежего кофе надо взять, чтобы получить 4,4 кг жареного?
   Решение: Потеря веса составляет $12\%$, значит, жареный кофе составляет $88\%$ от исходного. Пусть $x$ — масса свежего кофе:
   $0,88x = 4,4$
   $x = \frac{4,4}{0,88} = 5$ (кг)
   Ответ: 5.
2. Упростите алгебраические выражения:
   1. $\left(c-\frac{c^{3}+8}{2 c+c^{2}}\right) \cdot \frac{c}{(c-2)^{2}}+\frac{2}{2-c}$
      Решение:
      Разложим числитель дроби: $c^3 + 8 = (c + 2)(c^2 - 2c + 4)$
      Знаменатель: $2c + c^2 = c(c + 2)$
      Упростим дробь: $\frac{c^3 + 8}{2c + c^2} = \frac{(c + 2)(c^2 - 2c + 4)}{c(c + 2)} = \frac{c^2 - 2c + 4}{c}$
      Подставим в выражение:
      $\left(c - \frac{c^2 - 2c + 4}{c}\right) \cdot \frac{c}{(c - 2)^2} + \frac{2}{2 - c} = \frac{2c - 4}{c} \cdot \frac{c}{(c - 2)^2} - \frac{2}{c - 2} = \frac{2(c - 2)}{(c - 2)^2} - \frac{2}{c - 2} = \frac{2}{c - 2} - \frac{2}{c - 2} = 0$
      Ответ: 0.
   2. $(2-\sqrt{5}) \sqrt{9+4 \sqrt{5}}$
      Решение:
      Заметим, что $9 + 4\sqrt{5} = (\sqrt{5} + 2)^2$
      Тогда: $\sqrt{9 + 4\sqrt{5}} = \sqrt{5} + 2$
      Подставим в выражение:
      $(2 - \sqrt{5})(\sqrt{5} + 2) = 2\sqrt{5} + 4 - 5 - 2\sqrt{5} = -1$
      Ответ: $-1$.
3. Найдите знаки $a, b$, и знак дискриминанта квадратного трехчлена $y = ax^2 + bx + c$, исходя из его графика:
   Решение:
   • Ветви параболы направлены вниз $\Rightarrow a < 0$
   • Вершина параболы находится справа от оси $OY$ $\Rightarrow -\frac{b}{2a} > 0$, учитывая $a 0$
   • График пересекает ось $OX$ в двух точках $\Rightarrow D > 0$
   Ответ: $a 0$, $D > 0$.
4. Решите систему $\left\{\begin{array}{l}x^{2}+y^{2}=5 \\ x^{3} y+x y^{3}=10\end{array}\right.$
   Решение:
   Преобразуем второе уравнение: $xy(x^2 + y^2) = 10$
   Подставим $x^2 + y^2 = 5$: $xy \cdot 5 = 10 \Rightarrow xy = 2$
   Система принимает вид:
   $\begin{cases} x^2 + y^2 = 5 \\ xy = 2 \end{cases}$
   Решаем методом подстановки:
   $(x + y)^2 = x^2 + 2xy + y^2 = 5 + 4 = 9 \Rightarrow x + y = \pm 3$
   $(x - y)^2 = x^2 - 2xy + y^2 = 5 - 4 = 1 \Rightarrow x - y = \pm 1$
   Получаем системы:
   • $x + y = 3$, $x - y = 1$ $\Rightarrow (2, 1)$
   • $x + y = 3$, $x - y = -1$ $\Rightarrow (1, 2)$
   • $x + y = -3$, $x - y = 1$ $\Rightarrow (-1, -2)$
   • $x + y = -3$, $x - y = -1$ $\Rightarrow (-2, -1)$
   Ответ: $(2; 1)$, $(1; 2)$, $(-1; -2)$, $(-2; -1)$.
5. В каждую клетку таблицы $3 \times 3$ произвольно ставят крестик или нолик.
   1. Сколькими способами можно заполнить эту таблицу?
      Решение: Каждая из 9 клеток имеет 2 варианта заполнения. Всего: $2^9 = 512$
      Ответ: 512.
   2. В скольких случаях в первом столбце будут стоять одни крестики?
      Решение: Первый столбец фиксирован (3 крестика), остальные 6 клеток произвольны: $2^6 = 64$
      Ответ: 64.
   3. В скольких случаях по диагонали будут стоять одни нолики?
      Решение: Диагонали содержат 5 клеток (главная и побочная пересекаются в центре). Фиксируем их как нолики, остальные 4 клетки произвольны: $2^4 = 16$
      Ответ: 16.
   4. В скольких случаях во втором столбце будет стоять ровно один крестик?
      Решение: Выбор позиции крестика во втором столбце: $C(3,1) = 3$. Остальные 6 клеток (вне второго столбца) произвольны: $2^6 = 64$. Всего: $3 \cdot 64 = 192$
      Ответ: 192.
6. Из пункта А в пункт Б, расположенный в 24 км от А, одновременно отправились велосипедист и пешеход. Велосипедист прибыл в пункт Б на 4 часа раньше пешехода. Известно, что если бы велосипедист ехал с меньшей на 4 км/ч скоростью, то на путь из А в Б он затратил бы вдвое меньше времени, чем пешеход. Найдите скорость пешехода.
   Решение:
   Пусть $x$ — скорость пешехода (км/ч), $v$ — скорость велосипедиста.
   Из условий:
   • $\frac{24}{x} - \frac{24}{v} = 4$
   • $\frac{24}{v - 4} = \frac{1}{2} \cdot \frac{24}{x} \Rightarrow x = \frac{v - 4}{2}$
   Подставляем $x$ в первое уравнение:
   $\frac{48}{v - 4} - \frac{24}{v} = 4$
   Умножаем на $v(v - 4)$:
   $48v - 24(v - 4) = 4v(v - 4)$
   $24v + 96 = 4v^2 - 16v$
   $4v^2 - 40v - 96 = 0 \Rightarrow v^2 - 10v - 24 = 0$
   Корни: $v = 12$ (т.к. $v > 0$). Тогда $x = \frac{12 - 4}{2} = 4$
   Ответ: 4.
7. В равнобокую трапецию с основаниями 2 и 8 вписана окружность. Найдите ее радиус.
   Решение:
   Для вписанной окружности сумма оснований равна сумме боковых сторон: $2 + 8 = 10 \Rightarrow$ каждая боковая сторона равна 5.
   Высота трапеции: $h = \sqrt{5^2 - \left(\frac{8 - 2}{2}\right)^2} = \sqrt{25 - 9} = 4$
   Радиус окружности: $r = \frac{h}{2} = 2$
   Ответ: 2.