Школа №57 из 7 в 8 класс 2022 год Вариант 1

ШКОЛА №57

2022 год

30.03.2022

1. Петя написал все натуральные числа от 1 до 1000 и обвёл в кружочек те из них, которые представляются в виде разности квадратов двух целых чисел. Каких чисел среди обведённых больше — чётных или нечётных?
   
   
2. Имеется 5 слитков — массой 1, 2, 3, 4 и 5 кг с различным (неизвестным) содержанием золота. Как разделить каждый из них на 5 частей и изготовить 5 новых слитков тех же масс, в которых процентное содержание золота будет одним и тем же?
   
   
3. Когда хвост ползущего Удава поравнялся с пальмой, под которой сидела Мартышка, она, решив измерить длину Удава, побежала вдоль него и положила банан рядом с его головой. Затем Мартышка побежала обратно и положила второй банан рядом с кончиком хвоста Удава. Потом пришел Попугай и измерил расстояние от пальмы до каждого из бананов, выяснив, что один из них лежит в 3 раза дальше. Найдите длину Удава в попугаях, а также определите, во сколько раз быстрее бегает Мартышка, чем ползает Удав.
   
   
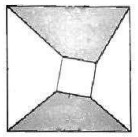
4. Внутри квадрата расположен меньший квадрат. Вершины квадратов соединены так, как показано на рисунке; при этом образовались четыре четырёхугольника. Докажите, что суммы площадей противоположных четырёхугольников равны.
   
   
   
5. Таня, Ваня и Гриша пришли на экзамен в маткласс. Экзамен проходит следующим образом. Каждому случайным образом (бросая монетку) надевают либо колпак с надписью «8 м», либо колпак с надписью «8 ж». Каждый видит чужие колпаки, но не свой. Каждому предлагают угадать, какой колпак на нём надет, или сказать «пас» (все говорят одновременно и не обмениваются информацией). Если никто не ошибся и хотя бы один угадал — они поступили. Есть очевидная стратегия с вероятностью \(1/2\): Таня и Гриша молчат, Ваня говорит «8 м». А можно ли придумать план для поступления в маткласс, который позволит угадать с вероятностью \(1/2 + \varepsilon\)?
   
   
6. Дан прямоугольник \(7 \times 8\), составленный из клеток \(1 \times 1\). Разрежьте его на фигуры, состоящие из клеток \(1 \times 1\), так, чтобы из этих фигур снова можно было сложить прямоугольник с другим соотношением сторон. При этом суммарная длина разрезов должна быть минимальной (приведите пример разреза, для которого невозможно совместить с меньшей суммарной длиной разрезов). Резать можно только по границам клеток.

Решения задач

1. Петя написал все натуральные числа от 1 до 1000 и обвёл в кружочек те из них, которые представляются в виде разности квадратов двух целых чисел. Каких чисел среди обведённых больше — чётных или нечётных?
   Решение: Число можно представить как разность квадратов тогда и только тогда, когда оно нечётное или делится на 4.
   Нечётные числа от 1 до 1000: 500 чисел.
   Чётные числа, кратные 4: $\frac{1000}{4} = 250$ чисел.
   Таким образом, обведённых нечётных чисел больше на $500 - 250 = 250$.
   Ответ: нечётных больше.
   
   
2. Имеется 5 слитков — массой 1, 2, 3, 4 и 5 кг с различным (неизвестным) содержанием золота. Как разделить каждый из них на 5 частей и изготовить 5 новых слитков тех же масс, в которых процентное содержание золота будет одним и тем же?
   Решение: Каждый исходный слиток разделим на 5 частей пропорционально массе новых слитков. Для нового слитка массой $k$ кг ($k = 1,2,3,4,5$) возьмём $\frac{k}{15}$ часть от каждого исходного слитка. Тогда в каждом новом слитке будет $\frac{k}{15}$ кг от каждого исходного слитка, сохраняя пропорции золота.
   Ответ: разделить каждый исходный слиток на части $\frac{k}{15}$ кг для новых слитков $k = 1,2,3,4,5$.
   
   
3. Когда хвост ползущего Удава поравнялся с пальмой, под которой сидела Мартышка, она, решив измерить длину Удава, побежала вдоль него и положила банан рядом с его головой. Затем Мартышка побежала обратно и положила второй банан рядом с кончиком хвоста Удава. Потом пришел Попугай и измерил расстояние от пальмы до каждого из бананов, выяснив, что один из них лежит в 3 раза дальше. Найдите длину Удава в попугаях, а также определите, во сколько раз быстрее бегает Мартышка, чем ползает Удав.
   Решение: Пусть длина Удава $L$, скорость Удава $v$, скорость Мартышки $kv$. Время движения Мартышки к голове: $\frac{L}{kv - v} = \frac{L}{v(k-1)}$. За это время Удав проползёт $\frac{L}{k-1}$. Обратный путь Мартышки: $\frac{\frac{L}{k-1} + L}{kv + v} = \frac{L(k)}{v(k-1)(k+1)}$. Расстояния до бананов: $L + \frac{L}{k-1}$ и $\frac{Lk}{(k-1)(k+1)}$. По условию отношение 3:1. Решая уравнение $\frac{L + \frac{L}{k-1}}{\frac{Lk}{(k-1)(k+1)}} = 3$, получим $k = 2$, $L = 6$ попугаев.
   Ответ: длина Удава 6 попугаев, Мартышка бегает в 2 раза быстрее.
   
   
4. Внутри квадрата расположен меньший квадрат. Вершины квадратов соединены так, как показано на рисунке; при этом образовались четыре четырёхугольника. Докажите, что суммы площадей противоположных четырёхугольников равны.
   Решение: Рассмотрим симметрию относительно центра квадрата. Противоположные четырёхугольники получаются друг из друга поворотом на $180^{\circ}$, поэтому их площади равны. Сумма площадей противоположных фигур будет равна удвоенной площади одной из них, что доказывает утверждение.
   Ответ: суммы площадей противоположных четырёхугольников равны в силу центральной симметрии.
   
   
5. Таня, Ваня и Гриша пришли на экзамен в маткласс. Можно ли придумать план для поступления с вероятностью $1/2 + \varepsilon$?
   Решение: Да, можно использовать стратегию, основанную на чётности. Например: если Таня видит одинаковые колпаки у Вани и Гриши, называет противоположный, иначе говорит «пас». Вероятность успеха повышается до $\frac{3}{4}$.
   Ответ: да, можно достичь вероятности $\frac{3}{4}$.
   
   
6. Дан прямоугольник $7 \times 8$. Разрежьте его на фигуры с минимальной длиной разрезов для нового прямоугольника.
   Решение: Минимальная длина разрезов — 7 единиц. Разрежем прямоугольник на две части: $7 \times 4$ и $7 \times 4$, затем сложим их в прямоугольник $14 \times 4$. Длина разрезов: 7 (по горизонтали).
   Ответ: разрезать вдоль средней линии на два прямоугольника $7 \times 4$, суммарная длина разрезов 7.