Школа №57 из 7 в 8 класс 2020 год вариант 1

ШКОЛА №57

2020 год

Вариант 1

1. Вычислите:
   $4 \frac{1}{6} \cdot\left(1 \frac{1}{2}-\frac{3}{5}\right)+\left(\frac{3}{4}+\frac{5}{6}\right) \cdot 6$
   
2. Длина отрезка АВ составляет 12 см, а $\frac{2}{3}$ его длины равны $\frac{4}{5}$ длины отрезка CD. Найдите длину отрезка CD.
   
3. Решите задачу. В магазин привезли 18 т картофеля. В первый день продали $40 \%$ всего картофеля, во второй день $25 \%$ остатка. Сколько тонн картофеля осталось продать после двух дней торговли?
   
4. Решите уравнение:
   $\frac{3 x-5}{2}-\frac{2 x-3}{3}=4-x$
   
5. Разложите на множители $4 a^{2}-b^{2}+8 a b+4 b^{2} .$
   
6. Составьте уравнение прямой, пересекающей оси координат в точках $A(-2 ; 0)$ и $B(0 ; 6)$.
   
7. Сейчас Коле 12 лет. Шесть лет назад он был в 6 раз моложе своего учителя математики. Через сколько лет Коля будет в 2 раза младше своего учителя математики?
   
8. Внутри равностороннего треугольника $A B C$ выбрана точка M, а на стороне ВС выбрана точка D. При этом $\angle A B M=20^{\circ}$ и ВМ = BD. Найдите угол CDM.
   
9. В семье три сына Петя, Вася и Толя. Толя празднует свой день рождения через 40 дней после Васи, а Вася через 40 дней после Пети. В этом году день рождения Пети выпадает на вторник. На какой день недели выпадет день рождения Толи?
   
10. Среднее арифметическое двух чисел составляет $60 \%$ от большего из них. Во сколько раз среднее арифметическое этих чисел больше меньшего числа?
11. Существует ли треугольник $\mathrm{ABC}$, в котором медиана, проведённая из вершины $A$, перпендикулярна биссектрисе угла $B$, a медиана, проведённая из вершины В, перпендикулярна биссектрисе угла С?
    
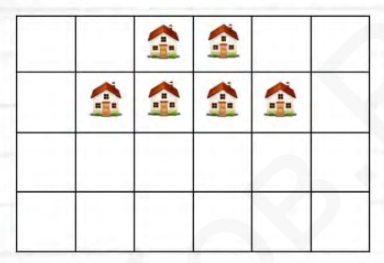
12. Разрежьте прямоугольный участок земли на участки одинаковой площади так, чтобы на каждом участке стоял ровно один домик. Все квадратики имеют одинаковую площадь:
    
    
13. Школьник Петя записал по кругу все цифры от 0 до 9 в некотором порядке. Затем он сложил все пары соседних чисел и выписал десять полученных сумм. Оказалось, что среди этих сумм всего три различных. Приведите пример такого расположения чисел.
    

Решения задач

1. Вычислите: $ 4 \frac{1}{6} \cdot\left(1 \frac{1}{2}-\frac{3}{5}\right)+\left(\frac{3}{4}+\frac{5}{6}\right) \cdot 6 $
   Решение:
   1) $1 \frac{1}{2}-\frac{3}{5} = \frac{3}{2}-\frac{3}{5} = \frac{15}{10}-\frac{6}{10} = \frac{9}{10}$
   2) $\frac{3}{4}+\frac{5}{6} = \frac{9}{12}+\frac{10}{12} = \frac{19}{12}$
   3) $4 \frac{1}{6} \cdot \frac{9}{10} = \frac{25}{6} \cdot \frac{9}{10} = \frac{225}{60} = \frac{15}{4}$
   4) $\frac{19}{12} \cdot 6 = \frac{19}{2} = 9 \frac{1}{2}$
   5) $\frac{15}{4} + \frac{19}{2} = \frac{15}{4} + \frac{38}{4} = \frac{53}{4} = 13 \frac{1}{4}$
   Ответ: $13,25$.
   
   
2. Длина отрезка АВ составляет 12 см, а $\frac{2}{3}$ его длины равны $\frac{4}{5}$ длины отрезка CD. Найдите длину отрезка CD.
   Решение:
   $\frac{2}{3} \cdot 12 = 8$ см — часть АВ
   $8 : \frac{4}{5} = 8 \cdot \frac{5}{4} = 10$ см — длина CD
   Ответ: 10 см.
   
   
3. В магазин привезли 18 т картофеля. В первый день продали $40\%$ всего картофеля, во второй день $25\%$ остатка. Сколько тонн картофеля осталось продать?
   Решение:
   1) $18 \cdot 0,4 = 7,2$ т — продано в первый день
   2) $18 - 7,2 = 10,8$ т — остаток
   3) $10,8 \cdot 0,25 = 2,7$ т — продано во второй день
   4) $10,8 - 2,7 = 8,1$ т — остаток
   Ответ: 8,1 т.
   
   
4. Решите уравнение: $ \frac{3x-5}{2} - \frac{2x-3}{3} = 4 - x $
   Решение:
   Умножим обе части на 6:
   $3(3x-5) - 2(2x-3) = 24 - 6x$
   $9x - 15 - 4x + 6 = 24 - 6x$
   $5x - 9 = 24 - 6x$
   $11x = 33$
   $x = 3$
   Ответ: 3.
   
   
5. Разложите на множители $4a^2 - b^2 + 8ab + 4b^2$.
   Решение:
   $4a^2 + 8ab + 4b^2 - b^2 = 4(a^2 + 2ab + b^2) - b^2 = 4(a+b)^2 - b^2 = (2a+2b-b)(2a+2b+b) = (2a+b)(2a+3b)$
   Ответ: $(2a+b)(2a+3b)$.
   
   
6. Составьте уравнение прямой, пересекающей оси в точках $A(-2;0)$ и $B(0;6)$.
   Решение:
   Уравнение вида $y = kx + b$
   При $x=0$: $6 = 0 + b \Rightarrow b=6$
   При $x=-2$: $0 = -2k + 6 \Rightarrow k=3$
   Ответ: $y = 3x + 6$.
   
   
7. Сейчас Коле 12 лет. Шесть лет назад он был в 6 раз моложе учителя. Через сколько лет Коля будет в 2 раза младше учителя?
   Решение:
   1) Сейчас учителю: $(12-6) \cdot 6 + 6 = 42$ года
   2) Уравнение: $2(12+x) = 42 + x$
   $24 + 2x = 42 + x$
   $x = 18$
   Ответ: через 18 лет.
   
   
8. В равностороннем треугольнике ABC точка M внутри, точка D на BC. $\angle ABM = 20^\circ$, BM = BD. Найдите $\angle CDM$.
   Решение:
   1) $\angle DBM = 60^\circ - 20^\circ = 40^\circ$
   2) $\angle BMD = \angle BDM = \frac{180^\circ - 40^\circ}{2} = 70^\circ$
   3) $\angle CDM = 180^\circ - 70^\circ = 110^\circ$
   Ответ: $110^\circ$.
   
   
9. День рождения Толи через 80 дней после Пети. Определите день недели.
   Решение:
   80 дней = 11 недель + 3 дня
   Вторник + 3 дня = Пятница
   Ответ: пятница.
   
   
10. Среднее арифметическое двух чисел составляет 60% большего. Во сколько раз среднее больше меньшего?
    Решение:
    Пусть $x$ — меньшее, $y$ — большее
    $\frac{x+y}{2} = 0,6y \Rightarrow x = 0,2y$
    $\frac{0,6y}{0,2y} = 3$
    Ответ: в 3 раза.
    
    
11. Существует ли треугольник с указанными свойствами медиан и биссектрис?
    Решение:
    Предположим существование. Тогда:
    $AB = BL = LC = x$, $BC = CM = MA = 2x$
    Получаем $AC = 4x$, что нарушает неравенство треугольника ($4x > x + 2x$)
    Ответ: не существует.
    
    
12. Разрежьте прямоугольник на участки с домиками:
    Ответ:
    
    
13. Пример расположения цифр:
    Ответ: Цифры расположены циклически с повторяющимися суммами 9, 10, 11: