Школа №57 из 7 в 8 класс

Продолжительность испытания — 2 часа. Тестовая часть состоит из задач 1–6, к которым нужно вписать только ответы. Для задач 7, 8 нужны не только ответы, но и развёрнутые решения.

1. Найдите значение выражения \[ \Bigl(\frac{2m+1}{2m-1} - \frac{2m-1}{2m+1}\Bigr)\;\colon\;\frac{4m}{10m-5} \quad\text{при }m=\frac{2}{3}. \]
   
   
2. Вычислите \[ \Bigl(\sqrt{4+\sqrt7} \;+\;\sqrt{4-\sqrt7}\Bigr)^{2}. \]
   
   
3. Решите неравенство \[ \frac{x-4}{\,x+3\,}\le 2. \]
   
   
4. Сколько граммов 3%-го и сколько граммов 8%-го растворов соли нужно взять, чтобы получить 500 г 4%-го раствора?
   
   
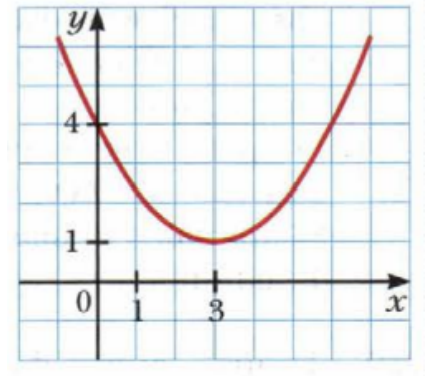
5. Запишите формулу функции \(y=f(x)\), график которой изображён на рисунке.
   
   
   
   
6. В прямоугольный треугольник вписана окружность. Найдите периметр треугольника, если точка касания делит гипотенузу на отрезки, равные 5 см и 12 см.
   
   
7. Из пункта \(A\) выехал велосипедист, а через 45 мин после этого в том же направлении выехал грузовик, который догнал велосипедиста на расстоянии 15 км от пункта \(A\). Найдите скорость велосипедиста и скорость грузовика, если скорость грузовика на 18 км/ч больше скорости велосипедиста.
   
   
8. В треугольнике \(ABC\) сторона \(AC\) равна 7, \(\angle BCA = 60^\circ\). Точка \(E\), лежащая на стороне \(BC\), удалена от вершины \(B\) на 6, \(F\) — точка пересечения \(AE\) с медианой \(BD\). Найдите сторону \(AB\), если \(BF : FD = 3 : 2\).

Решения задач

1. Задача 1. Найдите значение выражения: \[ \Bigl(\frac{2m+1}{2m-1} - \frac{2m-1}{2m+1}\Bigr)\;\colon\;\frac{4m}{10m-5} \quad \text{при } m=\frac{2}{3}. \]
   Решение: Упростим выражение: \[ \frac{(2m+1)^2 - (2m-1)^2}{(2m-1)(2m+1)} \cdot \frac{10m-5}{4m} = \frac{8m}{(4m^2 -1)} \cdot \frac{5(2m-1)}{4m} = \frac{10}{2m+1}. \] Подставляя \( m = \frac{2}{3} \): \[ \frac{10}{2 \cdot \frac{2}{3} +1} = \frac{10}{\frac{7}{3}} = \frac{30}{7}. \] Ответ: \(\frac{30}{7}\).
   
   
2. Задача 2. Вычислите: \[ \Bigl(\sqrt{4+\sqrt7} \;+\;\sqrt{4-\sqrt7}\Bigr)^{2}. \]
   Решение: Раскрывая квадрат суммы: \[ (4 + \sqrt7) + (4 - \sqrt7) + 2\sqrt{(4 + \sqrt7)(4 - \sqrt7)} = 8 + 2\sqrt{9} = 8 + 6 = 14. \] Ответ: 14.
   
   
3. Задача 3. Решите неравенство: \[ \frac{x-4}{x+3} \le 2. \]
   Решение: Преобразуем неравенство: \[ \frac{-x-10}{x+3} \le 0 \quad \Rightarrow \quad \frac{x+10}{x+3} \ge 0. \] Метод интервалов: \( x \in (-\infty, -10] \cup (-3, +\infty) \). Ответ: \( x \in (-\infty; -10] \cup (-3; +\infty) \).
   
   
4. Задача 4. Сколько граммов $3\%$-го и $8\%$-го растворов соли нужно взять, чтобы получить 500 г $4\%$-го раствора?
   Решение: Пусть \( x \) г — масса $3\%$-го раствора. Тогда: \[ 0.03x + 0.08(500 - x) = 0.04 \cdot 500 \quad \Rightarrow \quad x = 400. \] Ответ: 400 г ($3\%$) и 100 г ($8\%$).
   
   
5. Задача 5. Запишите формулу функции по графику.
   Решение: График — парабола с вершиной в точке \( (2, 1) \) и проходящая через точку \( (0, -3) \): \[ y = - (x - 2)^2 + 1 = -x^2 + 4x - 3. \] Ответ: \( y = -x^2 + 4x - 3 \).
   
   
6. Задача 6. Найдите периметр прямоугольного треугольника с вписанной окружностью.
   Решение: Гипотенуза \( c = 5 + 12 = 17 \) см. Катеты: \( 12 + 3 = 15 \) см и \( 5 + 3 = 8 \) см. Периметр: \[ P = 15 + 8 + 17 = 40 \text{ см}. \] Ответ: 40 см.
   
   
7. Задача 7. Найдите скорости велосипедиста и грузовика.
   Решение: Пусть скорость велосипедиста \( x \) км/ч: \[ \frac{15}{x} = \frac{15}{x + 18} + \frac{3}{4} \quad \Rightarrow \quad x = 12. \] Ответ: 12 км/ч (велосипедист), 30 км/ч (грузовик).
   
   
8. Задача 8. Найдите сторону \( AB \) треугольника.
   Решение: Используя координаты и теорему косинусов: \[ AB = \sqrt{7^2 + 14^2 - 2 \cdot 7 \cdot 14 \cdot \cos60^\circ} = 7\sqrt{3}. \] Ответ: \( 7\sqrt{3} \).