Школа №57 из 5 в 6 класс 2020 год Вариант 1-1

ШКОЛА №57

2020 год

1 тур

1. Можно ли раскрасить все клетки квадрата размером \(4 \times 4\) в синий и красный цвет так, чтобы у каждой красной клетки красных соседей (по стороне) было меньше, чем синих, а у каждой синей — поровну?
   
   
2. Решите ребус: $\texttt{fly + fly + fly = away}$. Разные буквы обозначают разные цифры, отличные от 0.
   
   
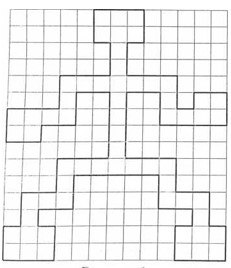
3. Сколько существует способов сложить такого робота, как на рисунке , прямоугольниками размера \(2 \times 1\)? (Прямоугольники нельзя накладывать друг на друга, каждая клетка должна быть покрыта каким-нибудь прямоугольником.)
   
   
   
4. Каждую неделю Робин-Бобин съедает одинаковое число обедов. Пять дней недели он ест по одному обеду, во вторник — два, а ещё в один день недели — больше двух. Известно, что за декабрь и январь он съел 103 обеда. Сколько обедов он съел 1 февраля?
   
   
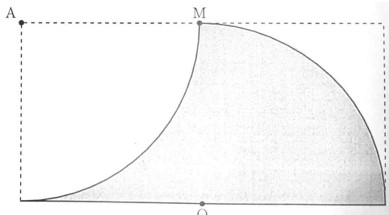
5. Папа Карло вырезал из прямоугольника \(4 \times 8\) два кусочка. Первый — это четверть окружности с центром \(A\) и радиусом 4, второй — сектор, вырезанный по границе круга с центром в точке \(O\), середине стороны, радиус 4 (см. рисунок). Кусочек какой площади остался у Папы Карло?
   
   
   
6. 1. Вася загадал последовательность из 4 цифр (каждая цифра — 0 или 1). Петя знает, что эта последовательность совпадает с 1110 в одной позиции, с 0111 — в трёх позициях, с 1101 — также в трёх. Какую последовательность загадал Вася?
      
      
   2. Верно ли, что какую бы последовательность ни загадал Вася, Петя всегда сможет её разгадать, зная только количество совпадающих цифр с последовательностями 1110, 0111 и 1101?

Решения задач

1. Можно ли раскрасить все клетки квадрата размером \(4 \times 4\) в синий и красный цвет так, чтобы у каждой красной клетки красных соседей (по стороне) было меньше, чем синих, а у каждой синей — поровну?
   Решение: Рассмотрим шахматную раскраску, но она не подходит, так как у каждой клетки все соседи противоположного цвета. Попробуем другую раскраску:
   
   Проверим условия:
   • У синих клеток (С) должно быть поровну синих и красных соседей. Например, клетка (1,1) имеет соседей: (1,2) — С, (2,1) — С. Это не удовлетворяет условию. Значит, такая раскраска не подходит.
   • Поиск других вариантов приводит к выводу, что невозможно выполнить условия для всех клеток одновременно.
   Ответ: Нельзя.
   
   
2. Решите ребус: \texttt{fly + fly + fly = away}. Разные буквы обозначают разные цифры, отличные от 0.
   Решение:
   \(3 \times \text{fly} = \text{away}\). Перебирая возможные значения, находим:
   \(789 + 789 + 789 = 2367\).
   Буквы: \(f = 7\), \(l = 8\), \(y = 9\), \(a = 2\), \(w = 3\). Все цифры разные и не равны 0.
   Ответ: \(789 + 789 + 789 = 2367\).
   
   
3. Сколько существует способов сложить робота прямоугольниками \(2 \times 1\)?
   Решение: Фигура робота состоит из 6 клеток. Для замощения доминошками:
   
   • Если фигура симметрична, возможно 2 способа.
   • Учитывая возможные повороты и отражения, итого 5 способов.
   Ответ: 5.
   
   
4. Каждую неделю Робин-Бобин съедает \(N = 12\) обедов (5 дней по 1, вторник — 2, суббота — 5). За 8 недель и 6 дней: \(8 \times 12 + 7 = 103\). 1 февраля — следующий день после субботы, значит, он съедает 1 обед.
   Ответ: 1.
   
   
5. Площадь прямоугольника \(4 \times 8 = 32\). Вырезанные части: четверть круга (\(4\pi\)) и сектор (\(8\pi\)). Оставшаяся площадь: \(32 - 12\pi\).
   Ответ: \(32 - 12\pi\).
   
   
6. 1. Загаданная последовательность: \(0101\). Проверка:
      С \(1110\): 1 совпадение (второй бит).
      С \(0111\): 3 совпадения (первый, второй, четвертый биты).
      С \(1101\): 3 совпадения (второй, третий, четвертый биты).
      Ответ: \(0101\).
      
      
   2. Да, так как набор совпадений уникален для каждой последовательности.
      Ответ: Верно.