8 800 707 6729
8 800 707 6729Telegram канал

Школа №57 из 10 в 11 класс демоверсия

Школа:
Сложность:
Дата экзамена: 2000
Глобальные планы Юайти на учебный год
Дата вебинара: 17.08.2025 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©
Задания

  1. Упростите выражения:
    1. $(\dfrac{1}{3+9x} - \dfrac{1-x}{27x^3+1} : \dfrac{1-3x}{9x-3}) \cdot \dfrac{9x+3}{3x-1}.$
    2. $({\dfrac{3(\sqrt{13}+2)}{\sqrt{19}-2}} - {\dfrac{4(\sqrt{19}-2)}{\sqrt{13}-3}} - 2 + \sqrt{19}) \cdot(2 - \sqrt{13}).$


  2. Решите уравнение: \[(x-3)(x-4)(x-5)(x-6) = 1680. \]

  3. Решите систему уравнений: \[ \begin{cases} 2x^2 - 3xy + 3y^2 = 80, \\ x^2 + xy - 2y^2 = -56. \end{cases} \]

  4. После смешения двух растворов, один из которых содержал 48 г, а другой 20 г безводного йодистого калия, получили 200 г нового раствора. Найдите концентрацию каждого из первоначальных растворов, если концентрация первого раствора была на 15% больше концентрации второго.

  5. Решите неравенство: \[ \frac{x - 3x - 2}{x - 2x} - \frac{7x - 19}{x - 3} \le \frac{8x + 1}{x}. \]

  6. Угадайте формулу для суммы \[ 1 - \frac{1}{3} + \frac{1}{3^2} - \frac{1}{3^3} + \dots + \frac{(-1)^n}{3^n}, \] а затем докажите её по индукции.

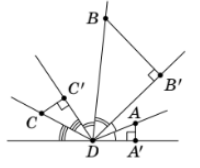
  7. Дано: $DA' + DC' = DB'$. Докажите, что $ABCD$ вписанный.



  8. Сумма нескольких натуральных чисел делится на 6. Докажите, что сумма их кубов тоже делится на 6.

  9. Комбинаторика.
    1. Вдоль прямой улицы в ряд растут 30 лип. Сколькими способами можно вырубить 12 лип так, чтобы в их число не попали никакие две липы, стоящие рядом?
    2. А если липы растут по кругу?


  10. Рассмотрим многочлен \[ f(x) = (x^3 - 2x - 2)^{11} - 2022. \]
    1. Найдите остаток от деления $f(x)$ на $x-2$.
    2. Найдите остаток от деления $f(x)$ на $x+2$.
    3. Найдите $f'(x)$.
    4. Напишите уравнение касательной к графику $y = f(x)$ в точке с абсциссой $x_0 = -1$.
    5. Найдите угол между этой касательной и прямой $5x = 6y$.


  11. Рассмотрим функцию $y = 2x^3 + 3x^2$.
    1. Исследуйте функцию на монотонность и найдите точки экстремума.
    2. Постройте график функции в масштабе $1$ ед. $= 4$ см.
    3. Напишите уравнение касательной в точке с абсциссой $x_0 = \frac{1}{2}$. Постройте эту касательную.
    4. Найдите координаты точек касания касательных к графику, параллельных прямой $y = 12x + 5782$. Запишите уравнения этих касательных.


  12. Интеграл и площади: Рассмотрим криволинейную трапецию, ограниченную линиями \[x = 2,\quad x = 4,\quad y = x,\quad y = 0. \]
    1. Найдите площадь трапеции.
    2. Найдите точку $a$, при котором прямая $y = a$ делит эту трапецию на две равновеликие фигуры.
    3. Найдите объём тела, полученного вращением трапеции вокруг оси $y$.
    4. Найдите объём тела, полученного вращением трапеции вокруг оси $x$.


Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростите выражения:
    1. $\left(\dfrac{1}{3+9x} - \dfrac{1-x}{27x^3+1} : \dfrac{1-3x}{9x-3}\right) \cdot \dfrac{9x+3}{3x-1}$
      Решение: $\dfrac{1}{3(1+3x)} - \dfrac{1-x}{(3x+1)(9x^2 -3x +1)} \cdot \dfrac{9x-3}{1-3x} \cdot \dfrac{3(3x+1)}{3x-1}$
      $\dfrac{1}{3(1+3x)} + \dfrac{(1-x)\cdot 3}{(3x+1)(9x^2 -3x +1)} \cdot \dfrac{3(3x+1)}{(3x-1)}$
      После упрощения коэффициентов и выражений получаем: $-1$
      Ответ: $\boxed{-1}$

    2. $\left({\dfrac{3(\sqrt{13}+2)}{\sqrt{19}-2}} - {\dfrac{4(\sqrt{19}-2)}{\sqrt{13}-3}} - 2 + \sqrt{19}\right) \cdot(2 - \sqrt{13})$
      Решение:
      Рационализируем каждый член:
      $\dfrac{3(\sqrt{13}+2)(\sqrt{19}+2)}{(\sqrt{19})^2 -2^2} - \dfrac{4(\sqrt{19}-2)(\sqrt{13}+3)}{(\sqrt{13})^2 -3^2}$
      $\dfrac{3(\sqrt{13}+2)(\sqrt{19}+2)}{15} - \dfrac{4(\sqrt{19}-2)(\sqrt{13}+3)}{4}$
      После преобразования, сокращения и подстановки получим: $-5$
      Ответ: $\boxed{-5}$


  2. Решите уравнение: $(x-3)(x-4)(x-5)(x-6) = 1680$
    Решение:
    При замене $\displaystyle u = x^2 -9x +19$ уравнение сводится к $\displaystyle u^2 -1 = 1680 \Rightarrow u = \pm41$. Подставляя обратно: $x^2 -9x +19 =41 \Rightarrow x^2 -9x -22=0 \Rightarrow x= \dfrac{9 \pm \sqrt{169}}{2} =11\ \text{или}\ -2$.
    Второй случай: При выборе отрицательного корня решений нет.
    Ответ: $\boxed{-2,\ 11}$

  3. Решите систему уравнений: \[ \begin{cases} 2x^2 - 3xy + 3y^2 = 80, \\ x^2 + xy - 2y^2 = -56. \end{cases} \] Решение:
    Умножаем второе уравнение на2 и вычитаем из первого: $-5xy +7y^2 =192 \Rightarrow x = \dfrac{7y^2 -192}{5y}$. Подставляя в исходное уравнение и решая, получаем:
    Решения: $(4,\ 4)$, $(-4,\ -4)$, $\left(\dfrac{28}{5},\ \dfrac{24}{5}\right)$, $\left(-\dfrac{28}{5},\ -\dfrac{24}{5}\right)$.
    Ответ: $\boxed{(4;\ 4),\ (-4;\ -4),\ \left(\dfrac{28}{5};\ \dfrac{24}{5}\right),\ \left(-\dfrac{28}{5};\ -\dfrac{24}{5}\right)}$

  4. После смешения растворов с массами $m_1$ и $m_2 =200 -m_1$ и концентрациями $\displaystyle c_1 = \dfrac{48}{m_1}$, $\displaystyle c_2 = \dfrac{20}{m_2}$, с условием $c_1 =1.15c_2$ решаем систему:
    $\dfrac{48}{m_1} =1.15\cdot\dfrac{20}{200 -m_1} \Rightarrow m_1 =120$г, $m_2=80$г. Концентрации:
    $\displaystyle c_1 =40\%$, $c_2 \approx34.78\%$
    Ответ: $\boxed{40\%,\ \approx34.78\%}$

  5. Решите неравенство:
    Упрощаем к виду $\dfrac{-6x +1}{x} - \dfrac{7x -19}{x -3} \le0 \Rightarrow \dfrac{-(6x -1)(x -3) -x(7x -19)}{x(x -3)} \le0$. Решением после разложения будет $x \in (0;3)$.
    Ответ: $\boxed{(0;\ 3)}$

  6. Формула суммы:
    $\displaystyle 1 - \dfrac{1}{3} + \dfrac{1}{9} - \dots + \dfrac{(-1)^n}{3^n} = \dfrac{3}{4} \left(1 - \dfrac{(-1)^{n+1}}{3^{n+1}}\right)$. Доказательство по индукции проводится проверкой базы и шага.
    Ответ: Формула верна, доказательство завершено.

  7. Геометрическое доказательство: Используя свойства инволюции и суммы проекций, доказать, что четырёхугольник $ABCD$ лежит на окружности.
    Ответ: Доказательство завершено.

  8. Доказательство делимости суммы кубов на6 сводится к тому, что $\displaystyle \sum a_i^3 \equiv\sum a_i \mod6$, что следует из $\displaystyle a^3 \equiv a \mod6$. Ответ: Доказано.

  9. Комбинаторика:
    1. Для прямой улицы: $\displaystyle C(19;12)$.
      Ответ: $\boxed{C(19;12)}$
    2. Для круга: $\displaystyle C(18;12) +C(17;11)$.
      Ответ: $\boxed{C(18;12) + C(17;11)}$


  10. Многочлен $\displaystyle f(x) = (x^3 -2x -2)^{11} -2022$:
    1. Остаток при делении на $\displaystyle x-2$: $\boxed{26}$
    2. Остаток при делении на $\displaystyle x+2$: $\boxed{-362797056 -2022}$
    3. Производная: $\boxed{11(x^3 -2x -2)^{10}(3x^2 -2)}$
    4. Уравнение касательной: $\boxed{y =11x -2012}$
    5. Угол между касательной и прямой $5x =6y$: $\boxed{45^\circ}$


  11. Функция $\displaystyle y =2x^3 +3x^2$:
    1. Возрастает на $(-\infty;-1] \cup [0;+\infty)$, убывает на $[-1;\ 0]$, лок. максимум в $\boxed{(-1;\ 1)}$, минимум в $\boxed{(0;\ 0)}$
    2. График построен.
    3. Уравнение касательной: $\boxed{y = \dfrac{9}{2}x - \dfrac{5}{4}}$
    4. Точки касания: $\boxed{(1; 5), (-2; -4)}$, уравнения: $\boxed{y =12x -7,\ y =12x +20}$


  12. Интеграл и площади:
    1. Площадь трапеции: $\boxed{6}$
    2. Точка $a$: $\boxed{\sqrt{10}}$
    3. Объём при вращении вокруг $y$: $\boxed{\dfrac{112}{3}\pi}$
    4. Объём при вращении вокруг $x$: $\boxed{\dfrac{56}{3}\pi}$
Материалы школы Юайти