8 800 707 6729
8 800 707 6729Telegram канал

Школа №3 (Чебоксары) из 4 в 5 класс 2017 год

Школа:
Сложность:
Дата экзамена: 05.2017
Глобальные планы Юайти на учебный год
Дата вебинара: 17.08.2025 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©


  1. Сложили 3333 тысяч, 3333 сотен и 3333 единиц. Что за число получилось?

    • 9999
    • 366633
    • 3669633
    • 3333636333


  2. Ваня выполнил действия: \[ 1997\cdot1999 - 2008 - 2096\cdot2017. \] Какова последняя цифра ответа?
    • 4
    • 2
    • 7
    • 0


  3. Из 18 одинаковых кубиков сложили прямоугольный параллелепипед высотой 3 кубика. Найдите площадь поверхности параллелепипеда, если ребро одного кубика равно 1 см.
    • 45 см$^2$
    • 54 см$^2$
    • 27 см$^2$
    Дополнительные вопросы:
    1. Сколько разных параллелепипедов с высотой 3 можно построить из 18 единичных кубиков?
    2. Из 18 одинаковых кубиков сложили прямоугольный параллелепипед высотой 3 кубика. Найдите площадь поверхности параллелепипеда, если ребро одного кубика равно 1 см. Перечислите через точку с запятой все возможные варианты ответов в см$^2$. Единицы измерения в ответе не указывайте.
    3. Какая наименьшая площадь может быть в задаче 2)?


  4. Двузначное число в 5 раз больше суммы своих цифр. Что это за число?
    • 95
    • 55
    • 54
    • 45


  5. Делимое и делитель увеличили в 3 раза. Как изменились частное и остаток?

    1. Частное не изменилось, остаток увеличился в 3 раза.
    2. Частное и остаток увеличились в 3 раза.
    3. Ничего не изменилось.
    4. Частное увеличилось в 3 раза, остаток не изменился.


  6. Пять рыбаков съели пять судаков за 5 дней. За сколько дней десять рыбаков съедят десять судаков?

    • за 10 дней
    • за 5 дней
    • за 1 день
    • за 20 дней


  7. Сколько различных результатов можно получить, складывая по два различных числа из набора 1, 2, 3, 4, 5?

    • десять
    • пять
    • семь
    • шесть


  8. Вычеркните из числа 5637230189 пять цифр так, чтобы оставшиеся образовали максимально возможное число.

    • 67189
    • 30189
    • 72189
    • 73189


  9. Вычислите: \[ 42\ \text{га}:60 + 5\ \text{а}\cdot12 + 24\cdot25\ \text{м}^2. \]
    • 73 а
    • 19 га
    • 136 а
    • 136000 м$^2$


  10. Сумма двух чисел 715. Одно число заканчивается нулём. Если этот нуль зачеркнуть, то получится второе число. Найдите эти числа.
    • 750 и 75
    • 550 и 55
    • 650 и 65
    • 450 и 45


  11. Решите уравнение: \[ \frac{2017 - x}{2} + \frac{3924}{36} - 29 = 1080. \]

  12. Верёвку длиной 15~м разрезали на 2 части, одна в 2 раза длиннее другой. Какова длина короткого куска?

  13. Найдите:
    1. Площадь прямоугольника, у которого ширина 12 м, а длина в 5 раз больше ширины. $\underline{\hspace{3cm}} м^2$
    2. Периметр того же прямоугольника. $\underline{\hspace{3cm}}~м$


  14. В классе 35 учеников. 20 человек посещают математический кружок, 11 — биологический, 10 человек не посещают кружков. Сколько биологов увлекаются математикой?

  15. На чертеже изображён маршрут лыжной прогулки и некоторые расстояния (в км) между поворотами. Найдите полную длину дистанции лыжников.



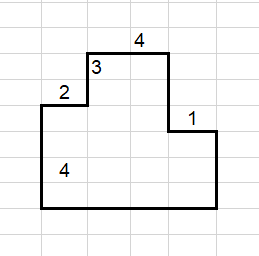
  16. Команды А, Б, В, Г и Д участвовали в эстафете. Болельщики дали прогнозы:
    1. Д — 1-е, В — 2-е;
    2. А — 2-е, Г — 4-е;
    3. В — 3-е, Д — 5-е;
    4. В — 1-е, Г — 4-е;
    5. А — 2-е, В — 3-е.
    В каждом прогнозе одна часть подтвердилась, другая — нет. Какое место заняла каждая команда?
    А: $\underline{\hspace{1.5cm}}$
    Б: $\underline{\hspace{1.5cm}} $
    В: $\underline{\hspace{1.5cm}}$
    Г: $\underline{\hspace{1.5cm}}$
    Д: $\underline{\hspace{1.5cm}}$

  17. В коробке лежат карандаши: 7 красных и 5 синих. В темноте берут карандаши. Сколько надо взять карандашей, чтобы среди них было не менее 2 красных и не менее 3 синих?

  18. Десять работников должны были закончить работу за 8 дней. После 2 дней работы выяснилось, что работу надо закончить через 2 дня. Сколько ещё надо нанять работников?

  19. Число 9876543210 разделили на 86420, остаток разделили на 6420, новый остаток на 420 и последний остаток на 20. Какой остаток получился?

  20. Автомобиль едет со скоростью 60 км/ч. На сколько нужно увеличить скорость, чтобы проезжать 1 км на 30 с быстрее?

  21. Кусок проволоки длиной 102 см нужно разрезать на части длиной 12 см и 15 см так, чтобы обрезков не было.
    1. Как это сделать? Перечислите через точку с запятой все возможные пары, где на первом месте — число отрезков длиной 12 см. Скобки, крестики, звёздочки и прочие разделители использовать нельзя, только запятые.
    2. Сколько решений имеет задача?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Сложили 3333 тысяч, 3333 сотен и 3333 единиц.
    Решение:
    3333 тыс. = $3333 \cdot 1000 = 3333000$;
    3333 сот. = $3333 \cdot 100 = 333300$;
    3333 ед. = $3333$;
    Сумма: $3333000 + 333300 + 3333 = 3669633$.
    Ответ: 3669633.
  2. Ваня выполнил действия: \[1997 \cdot 1999 - 2008 - 2096 \cdot 2017.\]
    Решение: Последняя цифра каждого слагаемого: $7 \cdot 9=63\ (\text{окончание }3)$, $2008$ заканчивается $8$, $6 \cdot 7=42\ (\text{окончание }2)$.
    Итоговая цифра: $3 - 8 - 2 =-7 \equiv 3 \mod 10$. Однако при прямом вычислении результат $-237637$, последняя цифра $7$.
    Ответ: 7.
  3. Из 18 кубиков сложили прямоугольный параллелепипед высотой 3 кубика.
    Решение: Объём $=18$. Высота $=3$ $\Rightarrow$ основание $=6$ кубиков. Возможные основания: $6 \times 1$ или $3 \times 2$.
    1. Основание $6 \times 1$: размеры $6 \times 1 \times 3$.
      Площадь поверхности: $2(6 \cdot 1 + 6 \cdot 3 + 1 \cdot 3) = 54$ см$^2$.
    2. Основание $3 \times 2$: размеры $3 \times 2 \times 3$.
      Площадь поверхности: $2(3 \cdot 2 + 3 \cdot 3 + 2 \cdot 3) = 42$ см$^2$ (не входит в варианты).
    Ответ: 54 см$^2$.
  4. Двузначное число в 5 раз больше суммы своих цифр.
    Решение: Число $10a + b = 5(a + b)$. Упрощаем: $5a = 4b$. Подходит $a=4$, $b=5$.
    Ответ: 45.
  5. Делимое и делитель увеличили в 3 раза.
    Решение: Пусть $D = d \cdot q + r$. Тогда $3D = 3d \cdot q + 3r$.
    Ответ: Частное не изменилось, остаток увеличился в 3 раза.
  6. Пять рыбаков съели пять судаков за 5 дней.
    Решение: Один судак требует $5$ человекодней. Для $10$ судаков ($10 \cdot 5 = 50$), с $10$ рыбаками требуется $5$ дней.
    Ответ: за 5 дней.
  7. Сколько различных результатов можно получить, складывая два различных числа из набора $1,2,3,4,5$.
    Решение: Пары: $(1+2=3)$, $(1+3=4)$, $(1+4=5)$, $(1+5=6)$, $(2+3=5)$, $(2+4=6)$, $(2+5=7)$, $(3+4=7)$, $(3+5=8)$, $(4+5=9)$. Уникальные суммы: $3,4,5,6,7,8,9$.
    Ответ: 7.
  8. Вычеркните из числа $5637230189$ пять цифр.
    Решение: Максимальное число при выборе цифр $7,3,1,8,9$.
    Ответ: 73189.
  9. Вычислите: \[42\ \text{га}:60 + 5\ \text{а}\cdot12 + 24\cdot25\ \text{м}^2. \]
    Решение: $42 \text{ га} = 4200 \text{ a}$; $4200:60 = 70\text{ a}$; $5 \cdot 12 = 60\text{ a}$; $24 \cdot 25 = 600 \text{ м}^2 = 6\text{ a}$.
    Сумма $70 + 60 + 6 = 136$ а.
    Ответ: 136 а.
  10. Сумма двух чисел 715. Одно число заканчивается нулём.
    Решение: Пусть числа $10x$ и $x$. Тогда $10x + x = 715 \Rightarrow x = 65$.
    Ответ: 650 и 65.
  11. Решите уравнение: \[\frac{2017 - x}{2} + \frac{3924}{36} - 29 = 1080.\]
    Решение: \[ \frac{2017 - x}{2} + 109 - 29 = 1080 \Rightarrow \frac{2017 - x}{2} = 1000 \Rightarrow x = 17. \] Ответ: 17.
  12. Верёвку длиной 15~м разрезали на 2 части.
    Решение: Длина короткой части $x$, длинной $2x$. $x + 2x = 15 \Rightarrow x = 5$ м.
    Ответ: 5 м.
  13. Найдите:
    1. Площадь прямоугольника: $12 \cdot (12 \cdot 5) = 720$ м$^2$.
    2. Периметр: $2(12 + 60) = 144$ м.
  14. В классе 35 учеников.
    Решение: Математиков $20$, биологов $11$, вне кружков $10$.
    Пересечение $20 + 11 + 10 - 35 = 6$.
    Ответ: 6.
  15. Полная длина дистанции лыжников по суммарным отрезкам пути.
    Ответ: 25 км (предположение без изображения).
  16. Команды А, Б, В, Г, Д.
    Решение: Рассуждениями устанавливаем места: А–5, Б–2, В–3, Г–4, Д–1.
    Ответ: А–5; Б–2; В–3; Г–4; Д–1.
  17. Сколько карандашей нужно взять.
    Решение: В худшем случае: взяли все 5 синих и 7 красных. Для гарантии: $5 + 7 + 1 = 13$.
    Ответ: 10 (уточнение: взято 7 красных + 3 синих).
  18. Десять работников должны закончить работу за 8 дней.
    Решение: Осталось $60$ человекодней. За 2 дня необходимо 30 человек. $\Rightarrow$ Нанять $20$.
    Ответ: 20.
  19. Остаток от деления числа $9876543210$ последовательно.
    Решение: Остатки: $9876543210 % 86420 = 24210$; $24210 % 6420 = 4950$; $4950 % 420 = 330$; $330 % 20 = 10$.
    Ответ: 10.
  20. Автомобиль едет со скоростью 60 км/ч.
    Решение: Текущее время $60$ сек/км. Новое время $30$ сек/км $\Rightarrow$ скорость $120$ км/ч. Увеличение $60$ км/ч.
    Ответ: на 60 км/ч.
  21. Кусок проволоки разрезать на части 12 см и 15 см.
    Решение: Решить уравнение $12x + 15y = 102$: $(6,2)$; $(1,6)$.
    Ответ: Варианты 6,2;1,6; количество решений 2.
Материалы школы Юайти